Rechenaufgaben zu Umfang und Fläche eines Kreises
Hier findest du Übungsaufgaben zum Berechnen des Umfangs und Flächeninhalts von Kreisen. Schaffst du sie alle?
- 1
Berechne die Kreisflächen der drei Kreise. Ziehe die richtigen Lösungen für den Flächeninhalt A in die Kreise.
- 2
Berechne den Flächeninhalt und Umfang eines Kreises mit dem
Radius
Radius .
- 3
Gib den Flächeninhalt eines Kreises mit dem Radius an.
Runde dein Ergebnis auf zwei Stellen nach dem Komma.
cm² - 4
- 5
Ermittle die fehlenden Größen in der Tabelle. Runde dabei auf eine Stelle nach dem Komma.
a)
b)
c)
d)
e)
Radius r
4,5 cm
0,7 mm
Durchmesser d
40,0 cm
5,6 m
Umfang U
92,4 m
- 6
Ermittle die fehlenden Größen in der Tabelle (auf die erste Dezimalstelle gerundet).
a)
b)
c)
d)
e)
Radius r
1,5 cm
33,0 cm
Durchmesser d
2,4 m
Umfang U
71,6 m
Flächeninhalt
12,56 cm²
- 7
Berechne den Durchmesser des Kreises mit dem Radius:
r = 3cm
r = 9cm
r = 14cm
- 8
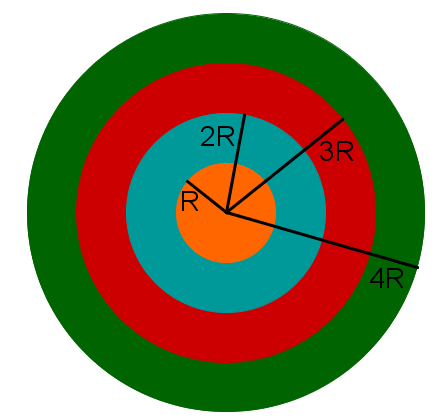
Begründe, wie sich jeweils Umfang und Flächeninhalt eines Kreises ändern, wenn man seinen Radius verdoppelt, verdreifacht bzw. vervierfacht.
- 9
Ein Kreis hat den Radius .
Welchen Umfang hat ein Kreis mit dem dreifachen Radius?
Welchen Flächeninhalt hat der Kreis mit dem dreifachen Radius?
- 10
Der Radius von einem Kreis beträgt .
Wie groß ist der Flächeninhalt ?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?