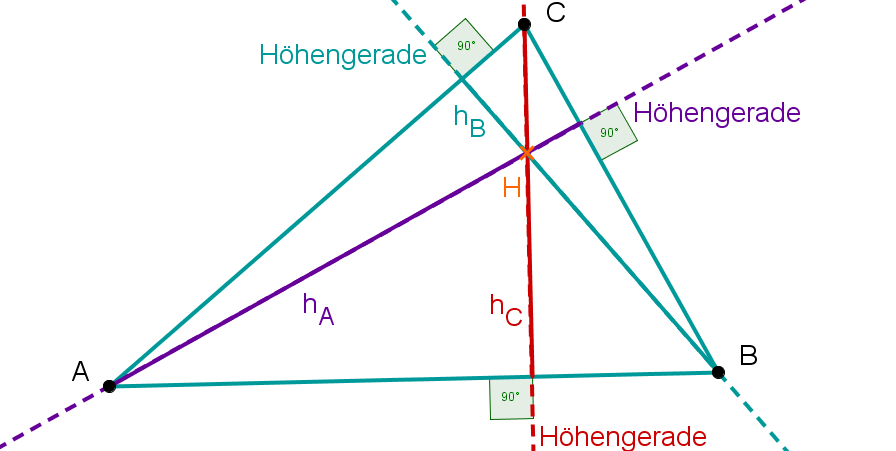
Konstruktion
Zeichne einen Kreis um einen Eckpunkt der so groß ist, dass er die gegenüberliegende Seite (oder die Verlängerung der Seite) zweimal schneidet.
Zeichne zwei gleich große Kreise durch die beiden Schnittpunkte, wobei der Radius so groß sein muss, dass sich die beiden Kreise schneiden.
Die Höhengerade ist die Gerade, die durch die beiden Schnittpunkte geht.
Anmerkung
Bei der Bestimmung des Höhenschnittpunktes reicht es aus, wenn man nur zwei Höhen konstruiert, da die Dritte auch durch den Schnittpunkt geht.
Bei stumpfwinkligen Dreiecken liegen zwei Höhen außerhalb des Dreiecks. (Nur die Höhe an der Ecke mit dem stumpfen Winkel liegt innerhalb). Somit liegt der Höhenschnittpunkt auch außerhalb des Dreiecks.
Video zum Thema gleichschenkliges Dreieck
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: