Für die Berechnung des Flächeninhalts eines beliebigen Dreiecks kennst du vielleicht schon diese Methoden: Flächeninhalt eines Dreiecks berechnen.
Wenn sich das Dreieck aber im Koordinatensystem befindet, gibt es noch zusätzliche Möglichkeiten:
Man kann mit der Determinante arbeiten.
(Man kann das Dreieck zum (achsenparallelen) Rechteck ergänzen und damit die Fläche berechnen. Die Erklärung dazu fehlt hier noch.)
Man kann das zweidimensionale Dreieck in den einbetten und mit dem Vektor- oder Kreuzprodukt arbeiten. Das wird in einigen Beispielaufgaben gezeigt.
Dreiecksfläche mit der Determinante berechnen
Voraussetzung: das Dreieck liegt in einem Koordinatensystem und es sind entweder die Koordinaten
der drei Eckpunkte (fange bei Schritt 1 an) oder
zwei Vektoren gegeben (fange bei Schritt 2 an).
Die Koordinaten der Eckpunkte lauten
Schritt 1: Berechnung von zwei Vektoren aus den Punkten
Nun berechnet man aus den Punktkoordinaten , und die Vektorkoordinaten und ("Spitze minus Fuß").
Beachte: Der Fußpunkt der Vektoren muss dabei gleich sein, in unserem Beispiel !
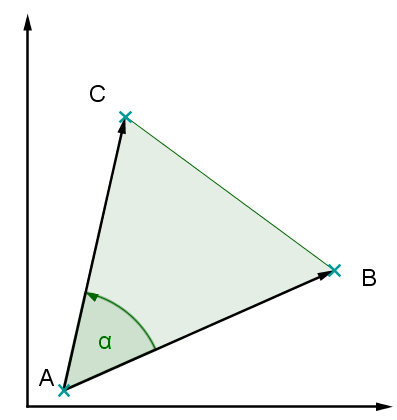
Schritt 2: Aufstellen der Determinante
Nun setzt du die beiden Vektoren und in die Determinante ein.
oder auch
Beachte die Reihenfolge der Vektoren: der erste Vektor muss gegen den Uhrzeigersinn (mathematischer Drehsinn; siehe Skizze) um den Fußpunkt gedreht auf dem zweiten Vektor liegen, damit der Flächeninhalt positiv wird!
Wenn man Betragsstriche um die Determinante setzt, ist die Reihenfolge nicht wichtig.
Wichtig ist es aber dann, wenn man einen Flächeninhalt in Abhängigkeit von berechnen soll!
Tipp: ohne vor der Determinante berechnest du den Flächeninhalt des von den Vektoren aufgespannten Parallelogramms.
Schritt 3: Berechnung des Werts der Determinante
Nun musst du nur noch den Wert der Determinante, und damit den Flächeninhalt des Dreiecks, nach der Formel
berechnen:
oder auch
Video
Laden
Dreiecksfläche durch Ergänzen zum Rechteck berechnen
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Flächenberechnung von Dreiecken im Koordinatensystem
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
