Wähle die richtige Antwort aus.
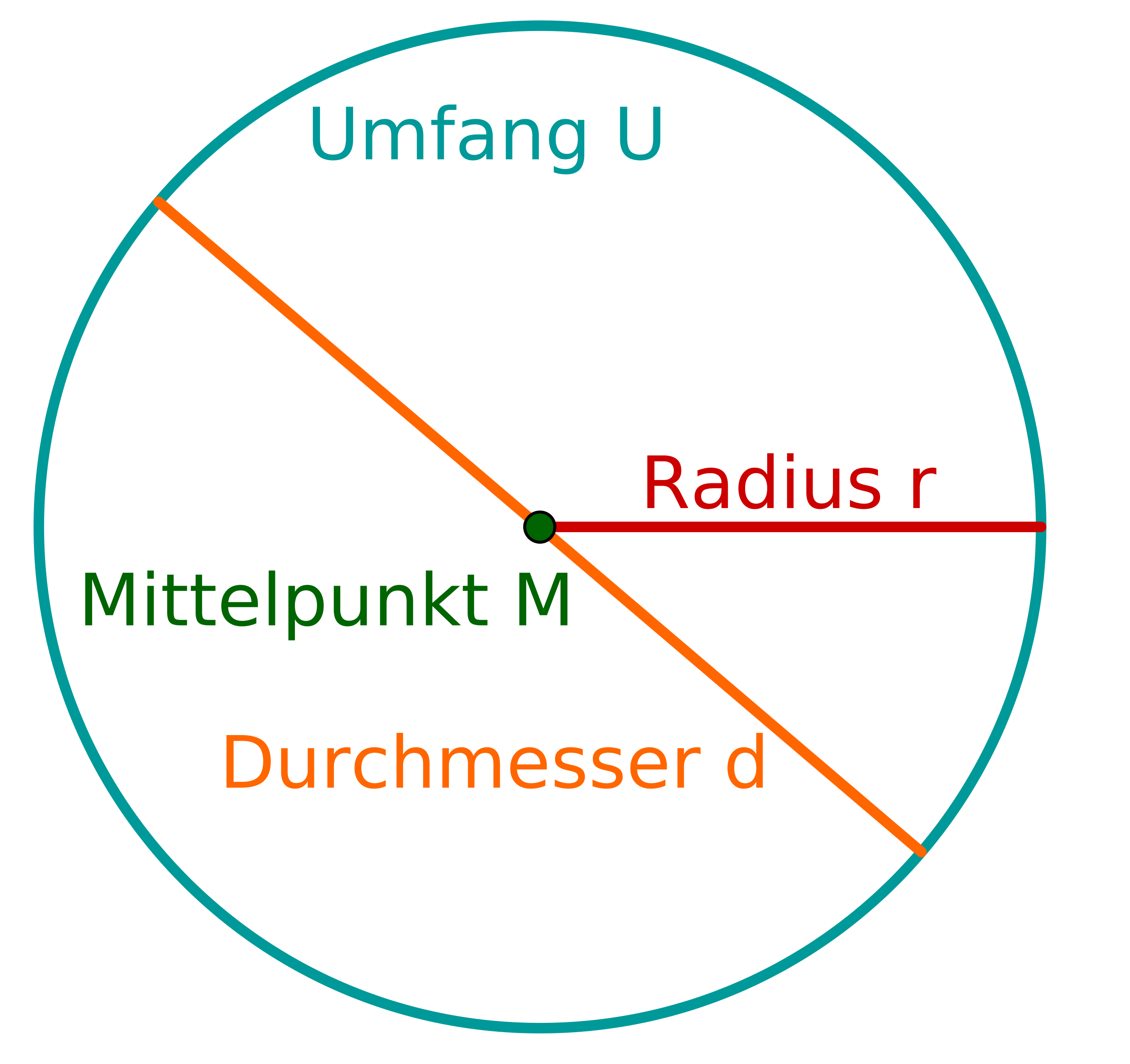
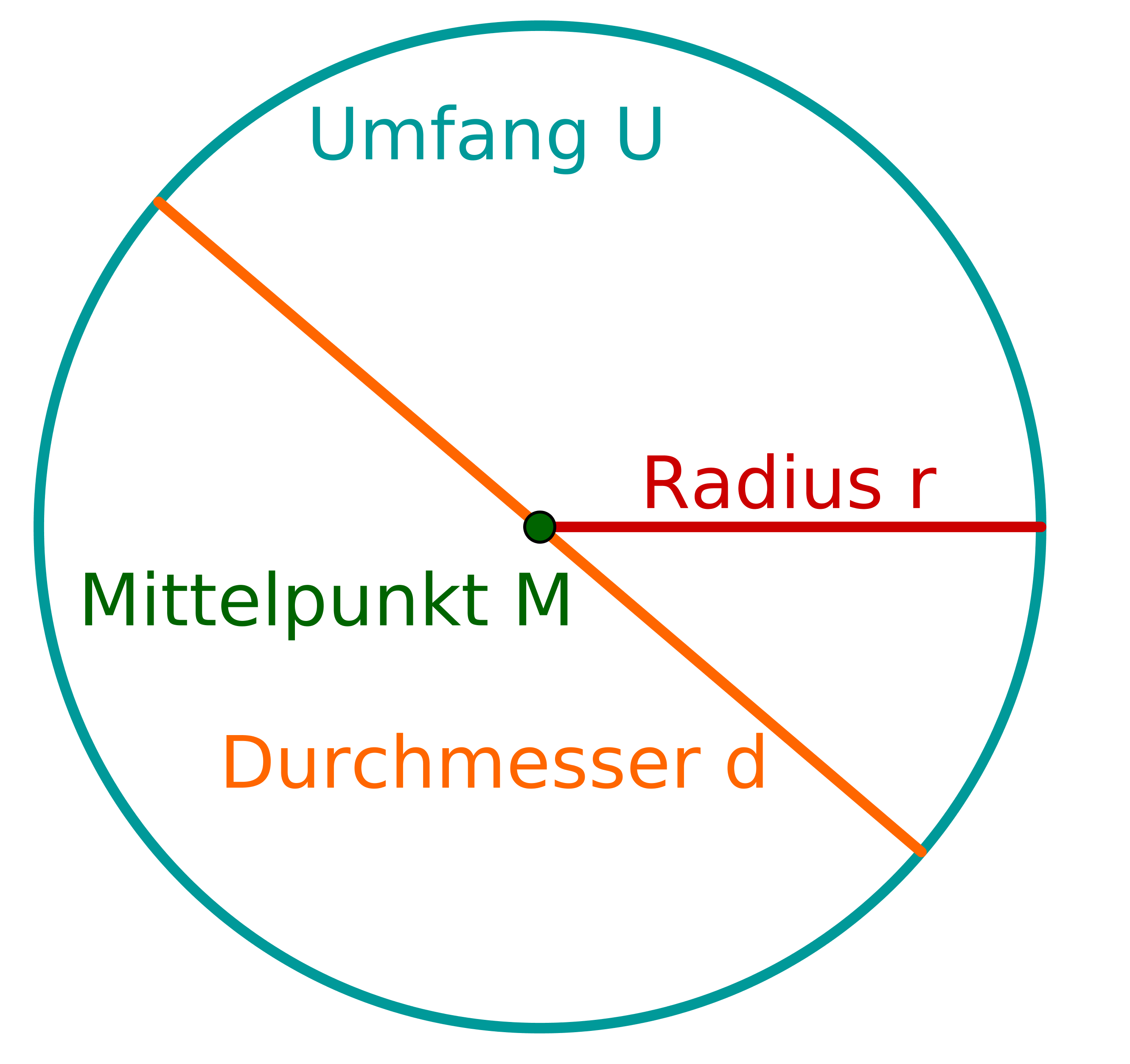
Wie berechnet man den Flächeninhalt von einem Kreis mit Radius ?
Welche Formel stimmt? (Mit ist der Flächeninhalt vom Kreis gemeint.)
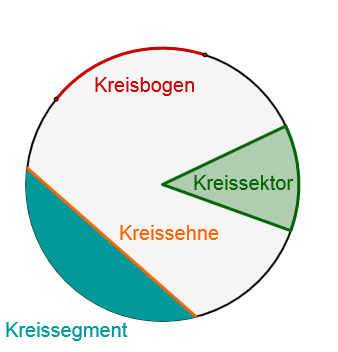
Auf welchem Bild ist ein Kreissegment dargestellt?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?