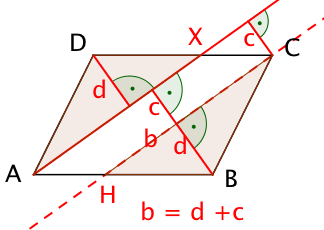
Quer durchs Parallelogramm
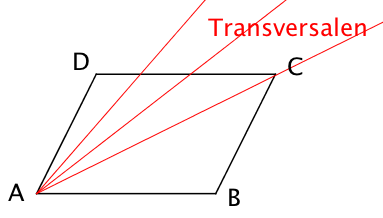
Eine Gerade "quer" durchs Parallelogramm, wie z.B. eine Diagonale, heißt eine Transversale.
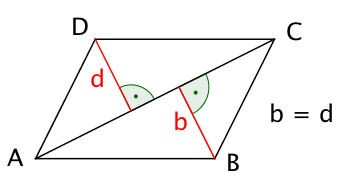
Begründe, warum die Eckpunkte B und D des Parallelogramms ABCD von der Diagonalen durch A und C gleichen Abstand haben.
Für eine durch den Eckpunkt A des Parallelogramms ABCD und einen beliebigen Punkt X der Seite [CD] verlaufende Transversale gilt:
Der Abstand des Punktes B zur Transversalen ist die Summe der Abstände der Eckpunkte C und D von ihr.
Begründe dies.
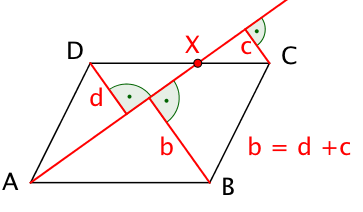
Was gilt für die Teilaufgabe b, wenn X = D?
Was gilt, wenn X = C?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?