Aufgaben zum Trapez
Wiederhole wichtige Grundlagen zum Trapez mit diesen Aufgaben. Hier lernst du, Trapeze zu erkennen, fehlende Seiten und andere Größen zu berechnen.
- 1
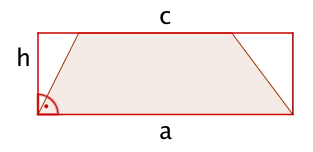
Sortiere das Trapez
Beim Zeichnen des Trapezes ist die Beschriftung durcheinander geraten.
Ordne die Beschriftung richtig zu.
Der Flächeninhalt vom Trapez wird berechnet. Welche der Formeln ist korrekt?
- 2
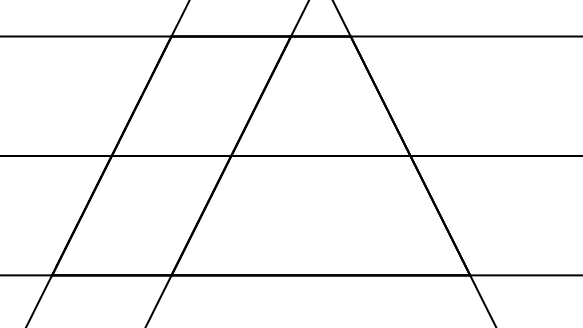
Augen auf!
Wie viele "echte" Trapeze (d.h. solche, die keine Parallelogramme sind), erkennst du in der gezeichneten Figur?
- 3
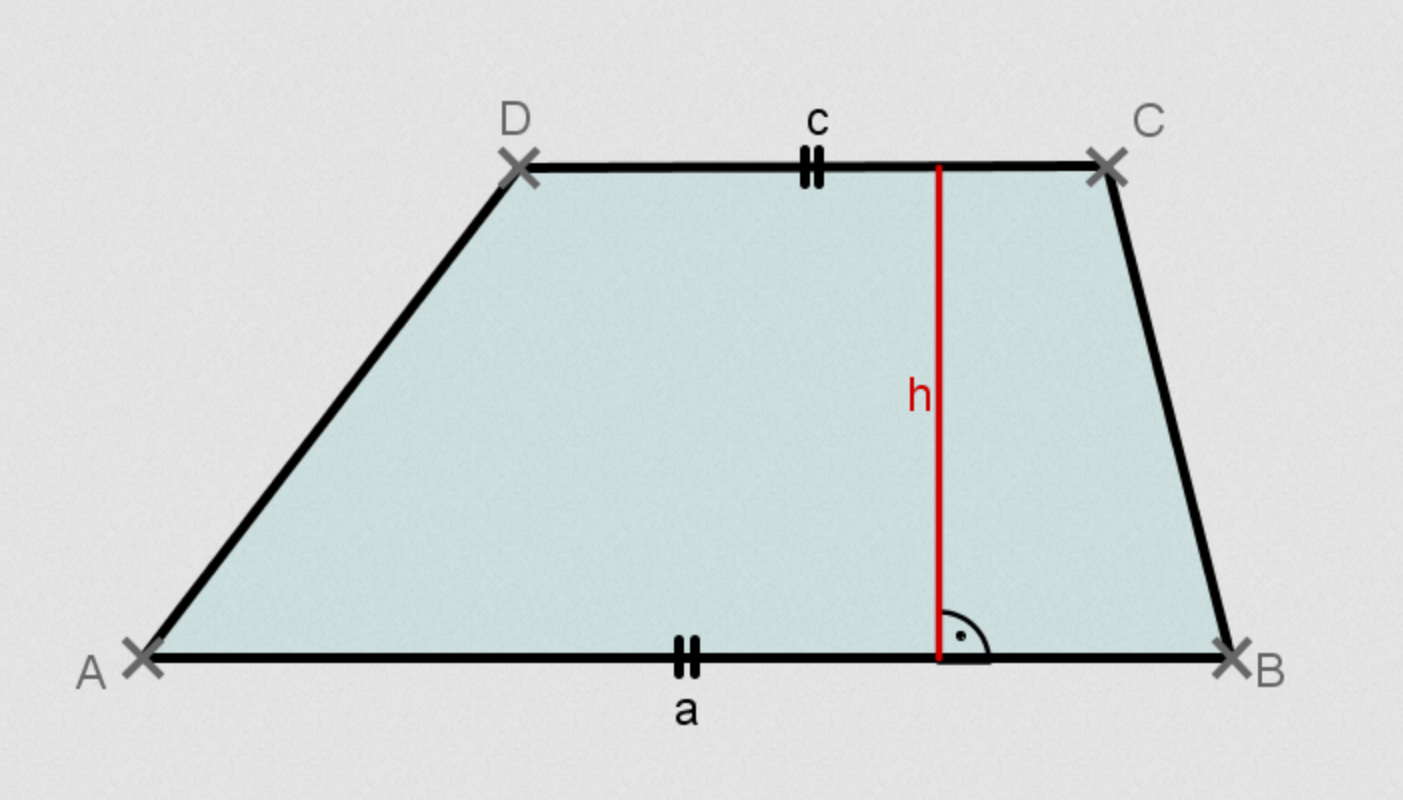
Die beiden parallelen Seiten eines Trapezes werden mit a und c bezeichnet, die Höhe mit h; für seinen Flächeninhalt gilt: .
Wie ändert sich der Flächeninhalt des Trapezes, wenn die Seite a um eine Längeneinheit verlängert und die Seite c um eine Längeneinheit verkürzt wird?
- 4
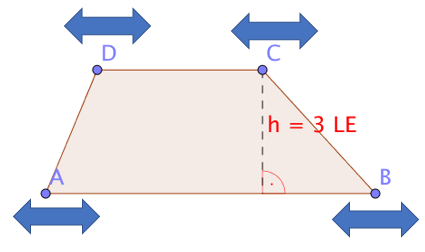
Vom Trapez zum Parallelogramm und zurück
Die Figur zeigt ein Trapez mit der gegebenen Höhe .
Welche der folgenden Aussagen treffen dann zu, wenn jeder der Eckpunkte längs seiner Grundseite beliebig weit nach links oder rechts verschoben werden kann?
- 5
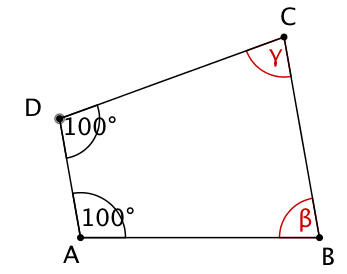
Winkelberechnungen am Trapez
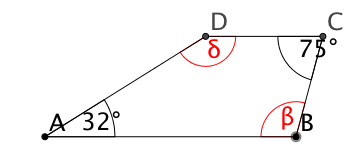
Im Trapez gelte , , . Berechne und !
Im Trapez gelte , , . Berechne !
Im Trapez gelte: . Berechne und !
- 6
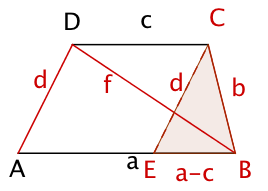
Konstruiere ein Trapez aus der gegebenen Länge der Differenz der beiden Grundseitenlängen , den Schenkellängen und sowie der Diagonalenlänge .
- 7
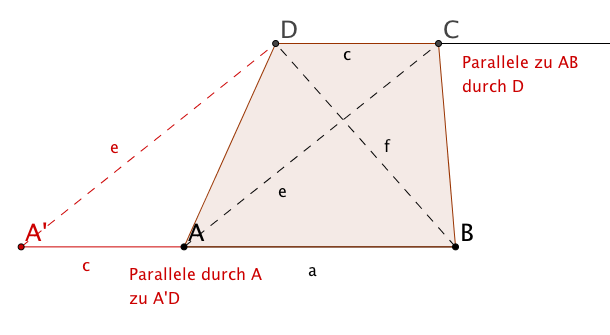
Konstruiere ein Trapez aus den Grundseitenlängen und sowie den Diagonalenlängen und .
- 8
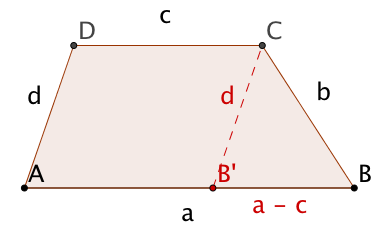
Konstruiere ein Trapez aus den Seitenlängen
.
- 9
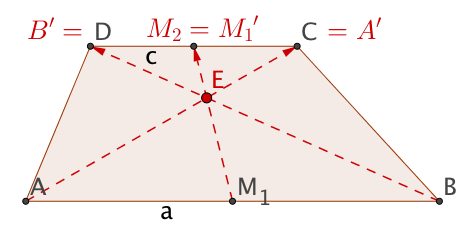
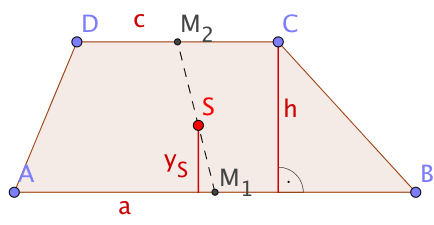
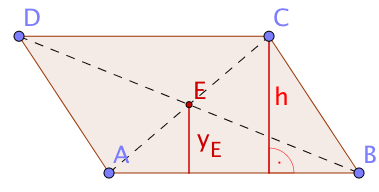
Meetingpoints am Trapez
Wie bei anderen Vierecken sind auch beim Trapez der Schnittpunkt der Diagonalen und der Schwerpunkt von besonderer Bedeutung.

Im Trapez mit den Grundseiten und und der Höhe sei der Schnittpunkt der Diagonalen und der Schwerpunkt des Trapezes.
Der Schwerpunkt eines Trapezes liegt auf der Verbindungstrecke der Mittelpunkte der Grundseiten (Mittenlinie) und hat von der Grundseite den Abstand
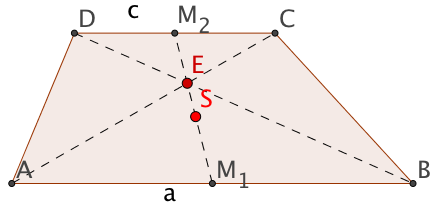
Beweise, dass die Mittenlinie eines jeden Trapezes durch den Schnittpunkt der Diagonalen geht.
Begründe, dass der Schwerpunkt und der Diagonlenschnittpunkt zusammenfallen, wenn das Trapez zu einem Parallelogramm wird.
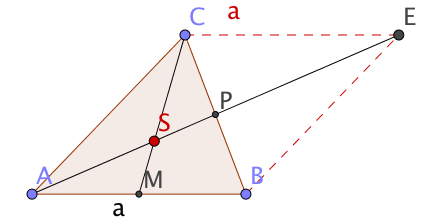
So konstruiert man den Schwerpunkt eines Trapezes:
Zeichne die Mittenlinie des Trapezes.
Verlängere über hinaus um die Strecke zum Endpunkt .
Verlängere über hinaus um die Strecke zum Endpunkt .
Der Schnittpunkt von mit ist der Schwerpunkt .
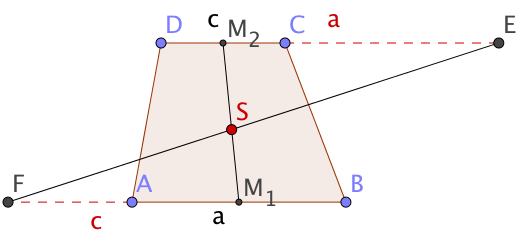
Begründe, warum für mit dieser Konstruktion der Schwerpunkt eines Dreiecks konstruiert wird.
- 10
Berechne jeweils die gesuchte Größe im Trapez.
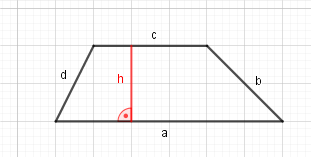
- cm²
- cm²
- dm²
- cm
- cm
- cm
- 11
Die Fläche eines Trapezes ist um kleiner als die Fläche eines Rechtecks, das über der größeren Grundlinie errichtet ist und die gleiche Höhe hat.
Wie groß sind die Grundlinien des Trapezes, wenn die eine um , die andere um länger ist als die Höhe?
Wie lang ist die Grundlinie eines Dreiecks, das dem Trapez flächen- und höhengleich ist?
m
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?