Ein Trapez ist
ein Viereck, bei dem
zwei gegenüberliegende Seiten parallel zueinander sind.
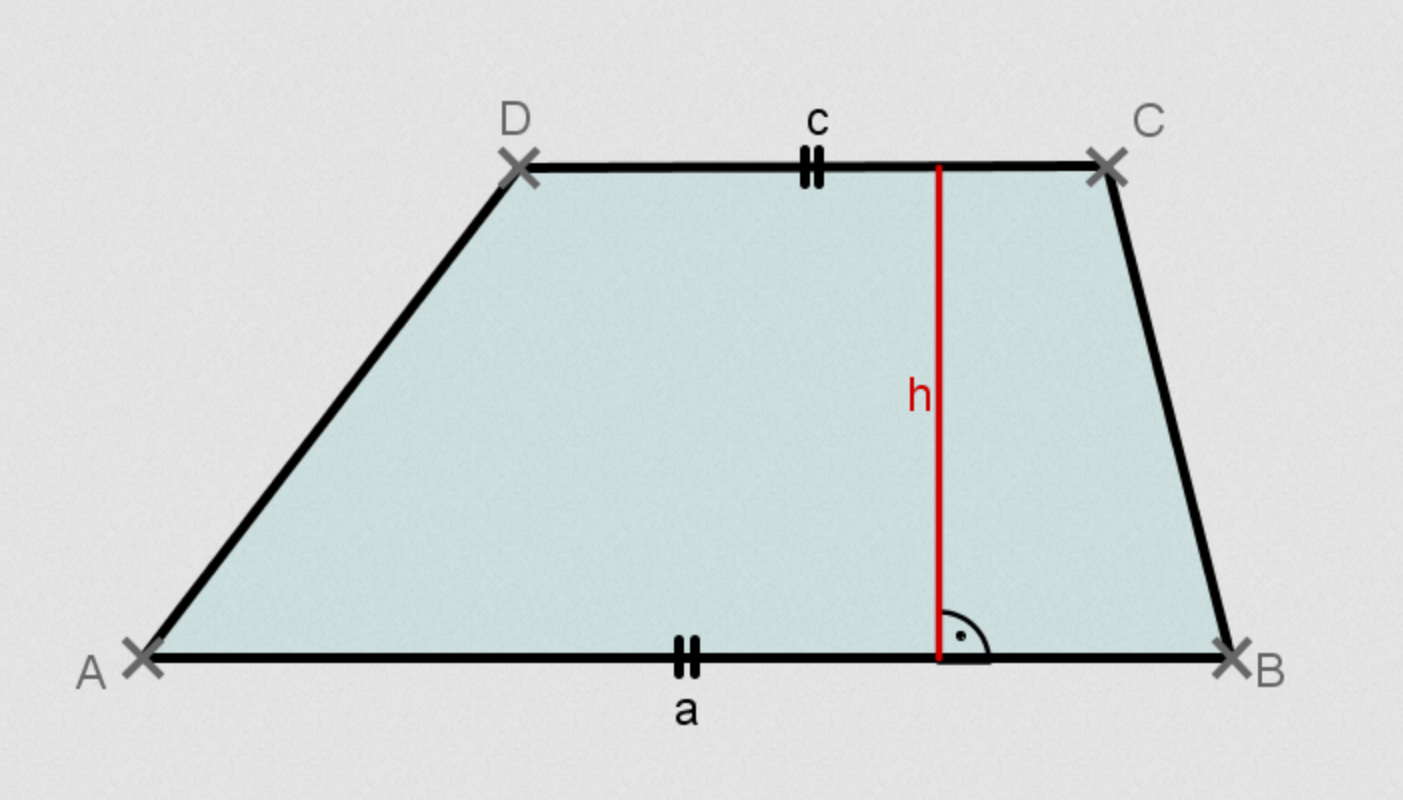
Eigenschaften des Trapezes
Seiten und Winkel
Seiten
Zwei gegenüberliegende Seiten sind im Trapez sicher zueinander parallel, die anderen beiden brauchen es nicht zu sein.
Allerdings ist natürlich nicht festgelegt, welche beiden Seiten die parallelen Seiten sind.
Links: Trapez mit
Rechts: Trapez mit
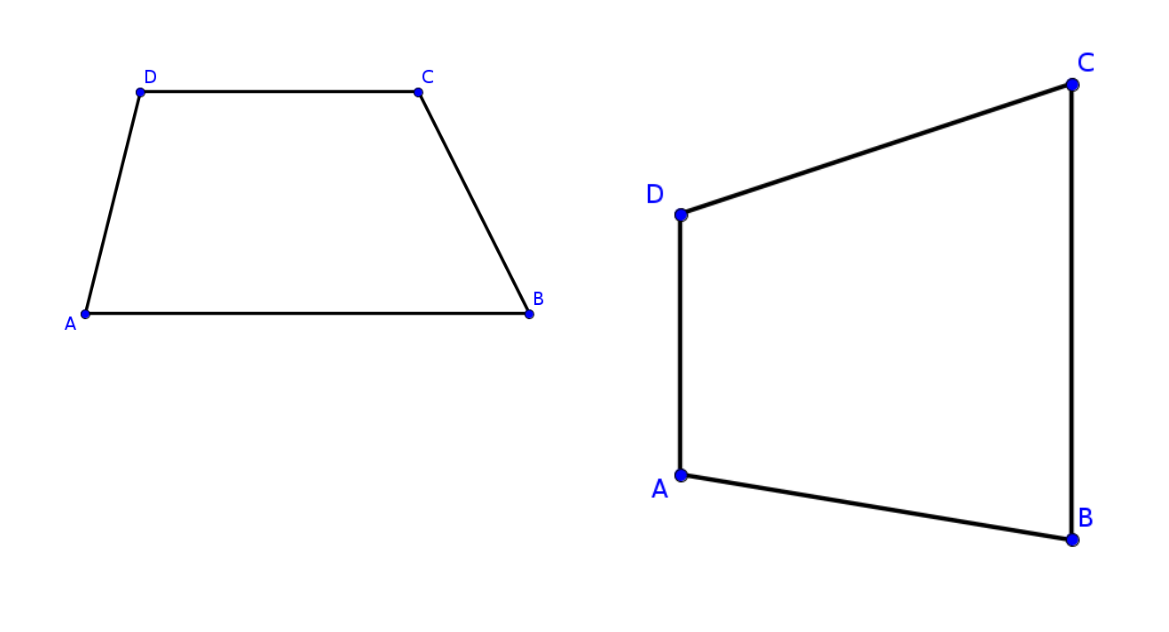
Die beiden parallelen Seiten nennt man manchmal auch die Grundseiten des Trapezes, die beiden anderen, nicht unbedingt parallelen Seiten, heißen die Schenkel des Trapezes.
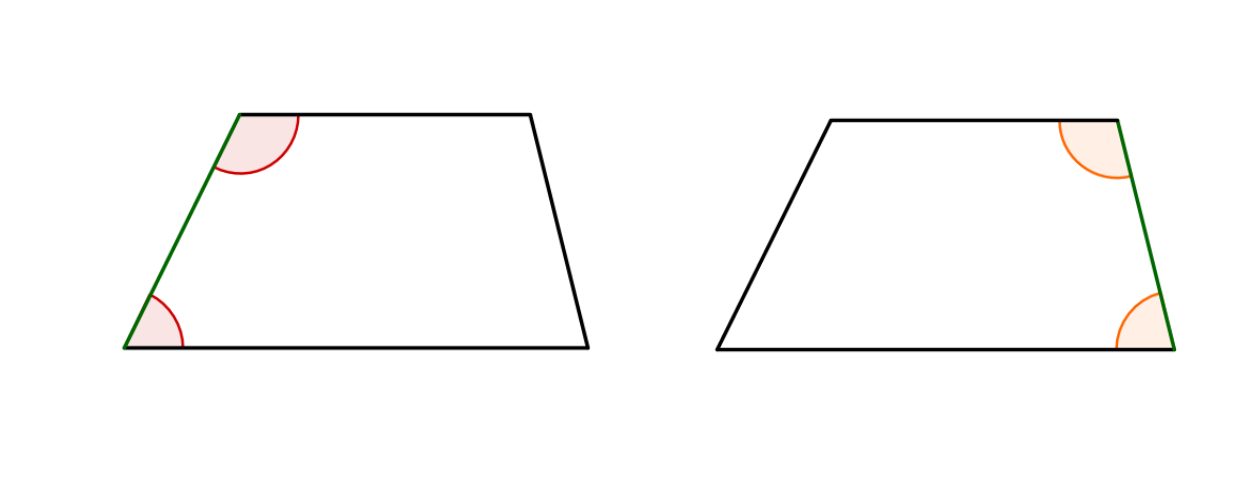
Winkel
In einem Trapez ergeben zwei auf derselben Seite eines Schenkels liegende Winkel zusammen 180°.
Fläche und Umfang
Flächeninhalt
Die Fläche eines Trapezes ist das Produkt von Höhe und der halben Summe der beiden zueinander parallelen Seiten:
Wenn man ein Trapez verdoppelt und das Zweite um 180° gedreht an das Erste legt, entsteht ein Parallelogramm mit der Grundlinie (a+c). Durch das Anwenden der Flächenformel eines Parallelogramms erhält man die oben genannte Formel.
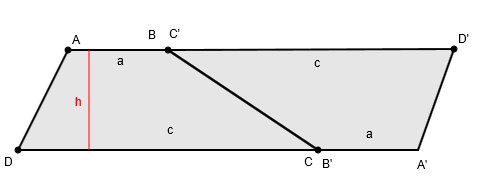
Umfang
Der Umfang eines Trapezes ist die Summe der Seitenlängen.
Spezielle Trapeze
Das Trapez ist bereits eine besondere Variante eines Vierecks. Wenn ein Trapez zusätzliche Eigenschaften erfüllt, entstehen noch speziellere Figuren. Diese sind
das Parallelogramm
die Raute
das Quadrat
das Rechteck.
Eine Übersicht aller Vierecke und wie sie zueinander in Beziehung stehen, findet man im Artikel Haus der Vierecke.
Laden
Übungsaufgaben
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Trapez
