Der Satz des Pythagoras stellt eine Beziehung zwischen den Seitenlängen eines rechtwinkligen Dreiecks her:
Die Summe der quadrierten Katheten (a und b) ist gleich dem Quadrat der Hypotenuse (c).
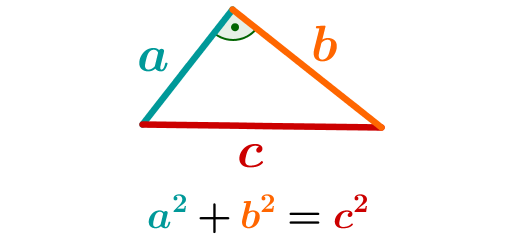
Die Formel gilt nur bei rechtwinkligen Dreiecken, wenn c die Hypotenuse ist!
Detaillierte Einführung
In diesem Video wird der Satz des Pythagoras sehr ausführlich erklärt.
Laden
Beispiel
Gegeben sind die beiden Katheten und eines rechtwinkligen Dreiecks.
Berechne die Hypotenuse .
| ↓ | Setze in den Satz des Pythagoras ein und rechne die rechte Seite aus. | ||
| ↓ | Ziehe die Wurzel | ||
(Bemerkung: Die Lösung scheidet aus, weil eine Länge nicht negativ sein kann.)
Wenn man nach einer Kathete sucht, muss man diese Formel umstellen.
Die Kathete lässt sich zum Beispiel berechnen mit
Video mit Beispielrechnungen
Laden
Pythagoras beschreibt auch Flächengleichheit
Für jede positive Zahl beschreibt die Fläche eines Quadrates mit der Seitenlänge . Genauso kann man sich und als Fläche von Quadraten vorstellen.
Der Satz des Pythagoras gibt somit auch einen Zusammenhang der Flächen über den Katheten und der Hypotenuse in einem rechtwinkligen Dreieck an. Anschaulich kann man dies an folgenden Applet erkennen.
In einem rechtwinkligen Dreieck ist die Summe der Flächen über den Katheten gleich groß wie die Fläche des Quadrats über der Hypotenuse.
Anwendungen
Rechtwinklige Dreiecke kommen sehr häufig vor. Damit hat der Satz des Pythagoras sehr viele Anwendungen.
Beispiele aus der Praxis
Berechnung von Streckenlängen in Gebäuden
Berechnungen an weiteren Figuren und Körpern
usw.
Als Hilfsmittel im Koordinatensystem
Berechnung des Abstandes zweier Punkte
Mathematische Spielereien
Wurzelschnecke (zum exakten Zeichnen von Strecken der Längen )
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Satzgruppe des Pythagoras
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
