Eine Matrix ist eine rechteckige Anordnung von Objekten, wie zum Beispiel Zahlen. Mithilfe von Matrizen können z.B. lineare Gleichungssysteme visualisiert und gelöst werden.
Aufbau
Eine Matrix der linksstehenden Form hat Zeilen und Spalten und daher Elemente.
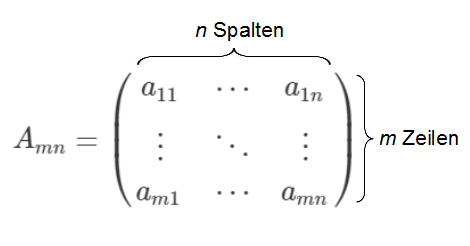
Aufstellen einer Matrix
Eine Matrix ist eine Anordnung von Vektoren in Zeilen oder Spalten.
Matrix-Vektor-Multiplikation
Eine -Matrix kann man wie folgt mit einem Spaltenvektor multiplizieren:
Allgemein multipliziert man eine Matrix mit einem Vektor auf diese Weise.
Vorgehensweise am Applett
Aufgaben
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
