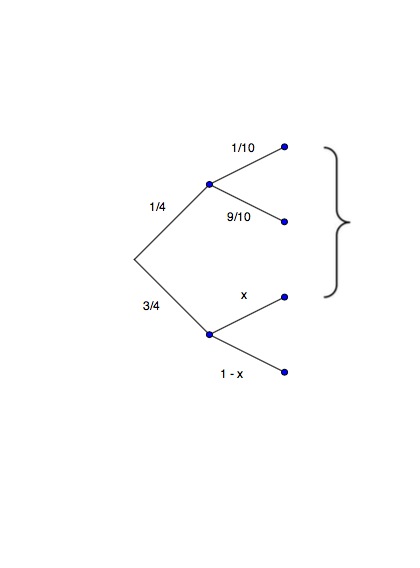
(Aus dem Leistungskurs-Abitur Bayern 2008/IV) In einem Molkereibetrieb wird Fruchtjoghurt hergestellt und in Becher abgefüllt. In dem Betrieb werden täglich gleich viele Becher der Sorten Erdbeere, Kirsche, Heidelbeere und Ananas abgefüllt. Bei einer Tagesproduktion, bei der 4 % der Becher einen defekten Deckel aufweisen, fällt auf, dass unter den Erdbeerjoghurtbechern sogar jeder zehnte Deckel fehlerhaft ist.
Bestimmen Sie den Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten. Klären Sie, ob es durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt gelingen kann, den angestrebten Qualitätsstandard von insgesamt höchstens 1 % Ausschussanteil einzuhalten.
Alle Becher mit defektem Deckel dieser Tagesproduktion werden aussortiert. Mit welcher Wahrscheinlichkeit enthält ein Becher, der zufällig aus den verbleibenden Bechern ausgewählt wird, Erdbeerjoghurt?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl → Was bedeutet das?