Übungsaufgaben 2. SA 11 Stochastik

1
Als Hausaufgabe sollten die Schüler der Klasse 6 b mindestens 100-mal würfeln und die relativen Häufigkeiten, mit denen die einzelnen Augenzahlen aufgetreten sind, mithilfe einer Tabelle oder eines Diagramms darstellen.
Am nächsten Tag vergleichen Manfred, Peter, Klaus und Christian ihre Ergebnisse:
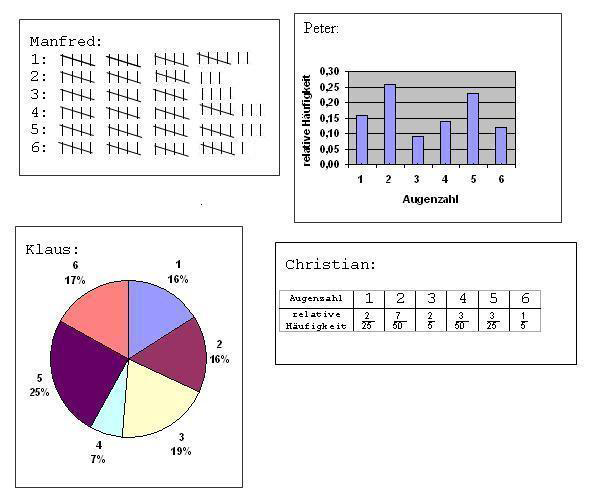
1. Nach einem kurzen Blick in Manfreds Heft sagt Christian: „Du hast wohl in der letzten Mathestunde nicht richtig aufgepasst!“ Wie kommt er dazu?
  Manfred hat in der letzten Mathestunde Quatsch gemacht.
  Manfred hat die relativen Häufigkeiten dargestellt.
  Manfred hat die absoluten Häufigkeiten dargestellt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Manfred hat nicht die relativen Häufigkeiten, sondern die absoluten Häufigkeiten angegeben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Klaus hat genau 200-mal gewürfelt. Wie oft hat er eine „6“ geworfen?
  Mal
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Klaus hat in $17 \%$ der Fälle eine $6$ gewürfelt. Du hast also die relative Häufigkeit gegeben, diese musst du jetzt mit der Gesamtanzahl an Würfen multiplizieren, um die absolute Häufigkeit zu erhalten:
  Klaus hat also insgesamt $34$ Mal eine $6$ gewürfelt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Peter betrachtet kurz die Diagramme und verkündet dann laut: „Christian hat von uns vier den besten Würfel. Bei ihm fällt am häufigsten die Sechs.“ Wie kommt Peter zu dieser Aussage? Glaubst auch du, dass Christian den besten Würfel hat?
  Christian hat wirklich den besten Würfel.
  Peter behauptet das, weil bei Christian die relative Häufigkeit mit $\frac15$ am größten ist.
  Christian hat nicht unbedingt einen besseren Würfel.
  Christian hat am meisten die 6 geworfen, weil er sich am meisten angestrengt hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Christian hat mit $\dfrac{1}{5}=0{,}2=20\,\%$ den höchsten Anteil von Würfen mit 6 Augen. Bei vielen Würfelspielen wäre er also im Vorteil.
  Ob Christian den besten Würfel hat, kann man aber so nicht sagen:
  Würfeln ist ein Zufallsexperiment, d.h. es ist "normal", dass nicht jeder gleich oft die 6 würfelt
  Die Jungen haben nicht gleich oft gewürfelt, das macht das Vergleichen noch schwieriger
  Es ist nicht in jedem Spiel besser viele 6er zu würfeln.
  Du hast noch weitere Ideen, warum Christian im Vorteil ist oder vielleicht auch nicht? Schreib sie in die Kommentare! :-)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Ein Viertel aller Schüler einer Klasse hat einen Hund, die Hälfte der Schüler hat eine Katze. Kein Schüler hat beide Haustiere. Ermittle den Anteil der Schüler, die keines dieser Haustiere haben.
$0$ Schüler hat keine Haustiere.
Die Hälfte $\left(\dfrac12\right)$ der Schüler hat keine Haustiere.
Ein Viertel $\left(\dfrac14\right)$ der Schüler hat keine Haustiere.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
Lösung durch eine Gleichung
Niemand in der Klasse hat beide Haustiere. Deshalb gibt es nur drei Situationen: Hund, Katze oder kein Haustier.
Die Summe der Anteile muss $100 ~\%$ , also $1$ ergeben.
$x$ bezeichnet den Anteil der Kinder, die keines dieser Haustiere haben.
$x+\underbrace{\dfrac{1}{4}}_{\text{Anteil mit Hund}}+\underbrace{\dfrac{1}{2}}_{\text{Anteil mit Katze}}=1$
$\displaystyle x$ $=$ $\displaystyle 1-\dfrac{3}{4}$
↓
nach x auflösen
$\displaystyle x$ $=$ $\displaystyle \dfrac14=0{,}25=25\,\%$
Darstellung in der Vierfeldertafel
Wenn du die Vierfeldertafel schon kennst, kannst du die Situation auch damit darstellen.
$H$
$\overline{H}$
$K$
0
$\frac{1}{2}$
$\frac{1}{2}$
$\overline K$
$\frac{1}{4}$
$\color{red}\frac{1}{4}$
$\frac{1}{2}$
$\frac{1}{4}$
$\frac{3}{4}$
1
(H: hat Hund, K: hat Katze)
Beim Ausfüllen der Vierfeldertafel ergibt sich der Wert $\frac{1}{4}$ für den Anteil "Kein Hund und keine Katze", bzw. $\bar{K}\wedge\bar{H}$ .
Beachte, dass kein Schüler beide Haustiere hat.
Du kannst die Aufgabe deshalb auch ohne eine Vierfeldertafel lösen.
3
In einer Schulklasse sind 28 Schüler, darunter 12 Mädchen. Bei einer Umfrage gaben 7 Mädchen und 8 Buben an, Sport sei ihr Lieblingsfach.
Ist das Fach Sport laut der Umfrage bei den Mädchen oder bei den Jungen in der Klasse beliebter?
Sport ist bei den Jungs beliebter.
Sport ist bei den Mädchen beliebter.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
Berechne Relative Häufigkeit
Anzahl Mädchen in der Klasse $=12$
Anzahl Jungen in der Klasse $=28-12=16$
Relative Häufigkeit der Mädchen, die am liebsten Sport mögen $=\frac7{12}\approx58\,\%$
Relative Häufigkeit der Jungen, die am liebsten Sport mögen $=\frac8{16}=\frac12=50\,\%$
$\Rightarrow$ Sport ist bei den Mädchen insgesamt beliebter.

	$H$	$\overline{H}$
$K$	0	$\frac{1}{2}$	$\frac{1}{2}$
$\overline K$	$\frac{1}{4}$	$\color{red}\frac{1}{4}$	$\frac{1}{2}$
	$\frac{1}{4}$	$\frac{3}{4}$	1

Ein Zufallsexperiment hat die vier Elementarereignisse

$\mathit\Omega=\{\omega_1,\omega_2,\omega_3,\omega_4\}$

Außerdem sind die Wahrscheinlichkeiten von drei Ereignissen $E_1$

bis $E_3$ gegeben.

$E_1:=\{\omega_1,\omega_2\}$ ; $P\left(E_1\right)=0{,}2$

$E_2:=\{\omega_3\}$ ; $P\left(E_2\right)=0{,}5$

$E_3:=\left\{\omega _4\right\}$ ; $P\left(E_3\right)=0{,}5$

Begründe, dass diese Wahrscheinlichkeitsverteilung unzulässig ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Die Summe aller Wahrscheinlichkeiten muss immer $1$ betragen, deswegen ist die Wahrscheinlichkeitsverteilung hier unzulässig, da sie $1{,}2$ beträgt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Addiere die Wahrscheinlichkeiten der Ereignisse
Ändere $P\left(E_3\right)$ so ab, dass die Wahrscheinlichkeitsverteilung zulässig ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Es muss gelten:
$P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right)=1$
Löse nach $P(E_3)$ auf.
$1-P\left(E_1\right)-P\left(E_2\right)=P\left(E_3\right)$
Setze die Werte aus der Angabe ein.
$1-0{,}2-0{,}5=0{,}3$
$\Rightarrow\;P\left(E_3\right)=0{,}3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Summe aller Ergebnisse muss 1 betragen.

Berechne $P\left(\left\{\operatorname{\omega}_1\right\}\right)$ unter der Voraussetzung, dass $\operatorname{\omega}_1$ mit einer doppelt so hohen Wahrscheinlichkeit auftritt wie $\operatorname{\omega}_2$ .

5
Welches der folgenden Zufallsexperimente ist ein Laplace-Experiment?
Begründe deine Entscheidung.
Werfen einer Münze
Werfen eines Würfels, der mit den Zahlen $1{,}2,3{,}4,5{,}2$ versehen ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Werfen eines Würfels, der mit den Zahlen $1{,}2,3{,}4,5{,}2$ versehen ist.
Dies ist kein Laplace-Experiment, da die Elementarereignisse nicht alle die gleiche Wahrscheinlichkeit haben.
Es ist zwar
für $\omega \in A = \left\{1{,}3,4{,}5\right\}$
(Kurzschreibweise für: $P(\left\{1\right\})=P(\left\{3\right\})=P(\left\{4\right\})=P(\left\{5\right\})=\frac16$ ),
d.h. man würfelt mit einer Wahrscheinlichkeit von $\frac16$ eine $1{,}3,4 \, \text{oder} \, 5$ ,
aber die Wahrscheinlichkeit eine $2$ zu würfeln, ist $P(\left\{2\right\})=\frac26 \ne \frac16$ .
Die $2$ kommt nämlich zweimal in der Grundmenge $\Omega= \left\{1{,}2,3{,}4,5{,}2\right\}$ vor.
Werfen einer Münze
Dies ist ein Laplace-Experiment.
Denn die Wahrscheinlichkeit Kopf oder Zahl zu würfeln, ist jeweils $\frac12$ , so dass alle Elementarereignisse die gleiche Wahrscheinlichkeit haben. Solche Münzen werden daher oft als Laplace-Münzen bezeichnet.
Bei einem Laplace-Experiment müssen alle Ergebnisse gleich wahrscheinlich sein.
6
Welches der folgenden Zufallsexperimente ist kein Laplace-Experiment?
Ziehen einer Kugel aus einer Urne mit 6 weißen und 4 schwarzen Kugeln
Ziehen einer Karte aus einem gewöhnlichen Set Spielkarten mit 52 Karten
Werfen eines Würfels mit den Zahlen $1{,}3,5{,}7,9{,}11$ versehen
Ziehen einer Kugel aus einer Urne mit unterschiedlichen 10 Kugeln
Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Werfen eines Würfels mit den Zahlen $1{,}3,5{,}7,9{,}11$ versehen.
Dies ist ein Laplace-Experiment, denn $P(\omega)=\frac16$ für alle $\omega \in \Omega$ , wobei $\Omega= \left\{1{,}3,5{,}7,9{,}11\right\}$ . Die Elementarereignisse haben also alle die gleiche Wahrscheinlichkeit.
Ziehen einer Karte aus einem Kartenspiel mit 52 Karten
Dies ist ein Laplace-Experiment, da die Wahrscheinlichkeit für das Ziehen jeder einzelnen Karte $\frac{1}{52}$ beträgt.
Ziehen einer Kugel aus einer Urne mit 10 Kugeln
Dies ist ein Laplace-Experiment.
Hier unterscheidetman wiederum gedanklich die $10$ einzelnen Kugeln, sodass jede Kugel mit einer Wahrscheinlichkeit $\frac{1}{10}$ gezogen wird.
Ziehen einer Kugel aus einer Urne mit 6 weißen und 4 schwarzen Kugeln
Dies ist kein Laplace-Experiment, da die Elementarereignisse nicht alle gleich wahrscheinlich sind.
Die Wahrscheinlichkeit eine weiße Kugel aus der Urne zu ziehen, beträgt nämlich $\frac{6}{10}=\frac{3}{5}$ und die Wahrscheinlichkeit eine schwarze Kugel aus der Urne zu ziehen, ist $\frac{4}{10}=\frac{2}{5}$ .
Bei einem Laplace-Experiment müssen alle Ergebnisse gleich wahrscheinlich sein.
7
Gegeben seien folgende Zufallsexperimente:
Zufallsexperiment 1
Drehen des folgenden Glücksrades:
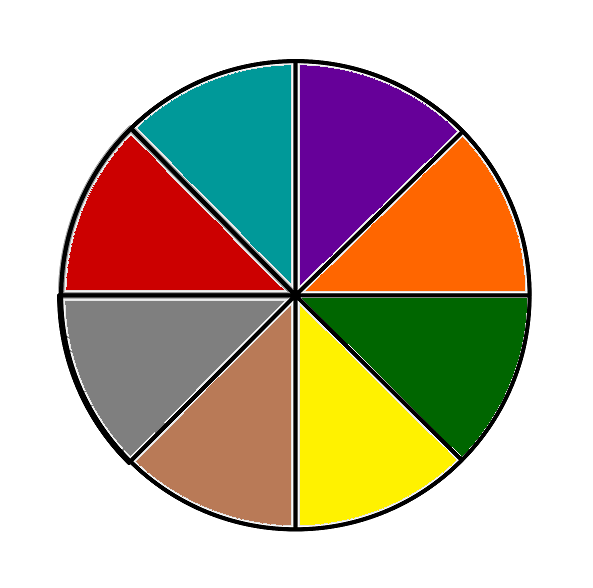
Zufallsexperiment 2
Drehen des folgenden Glücksrades:
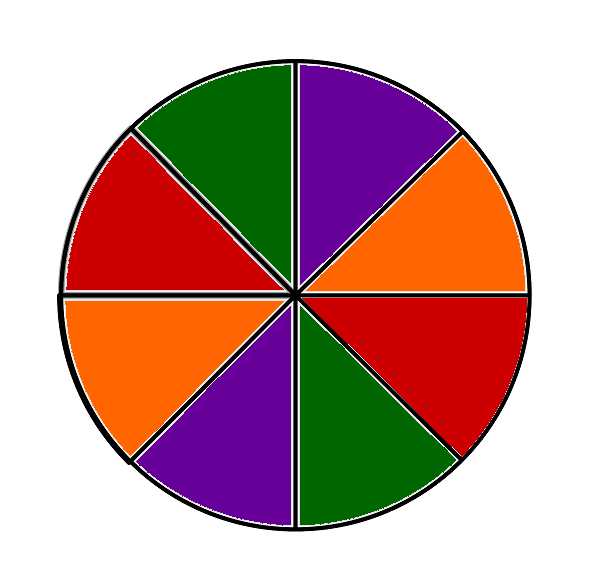
Zufallsexperiment 3
Drehen des folgenden Glücksrades:
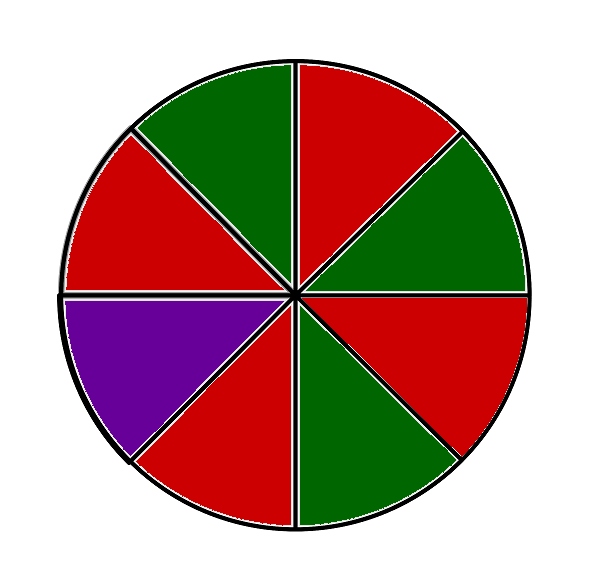
Wähle alle Zufallsexperimente, die nicht zu einem Laplace-Experiment gehören.
Zufallsexperiment 3
Zufallsexperiment 1
Zufallsexperiment 2
Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Zufallsexperiment 1
Dies ist ein Laplace-Experiment.
Denn alle Felder sind gleich groß und haben jeweils unterschiedliche Farben.
Somit haben alle Elementarereignisse "Drehe das Feld mit der Farbe $x$ " die gleiche Wahrscheinlichkeit.
Zufallsexperiment 2
Dies ist ein Laplace-Experiment.
Denn alle Felder sind gleich groß und jede Farbe kommt genau 2 Mal vor.
Somit sind die Wahrscheinlichkeiten aller Elementarereignisse "Drehe das Feld mit der Farbe $x$ " gleich groß.
Zufallsexperiment 3
Dies ist kein Laplace-Experiment.
Zunächst einmal stellt man fest, dass alle Felder gleich groß sind. Aber es gibt hier z.B. 4 rote und 3 grüne Felder, sodass das Ereignis "Man dreht das Feld mit der Farbe rot" und das Ereignis "Man dreht das Feld mit der Farbe grün" nicht gleich wahrscheinlich sein können. Die Wahrscheinlichkeit, ein rotes Feld zu drehen, ist nämlich größer als ein grünes Feld zu drehen.
Ähnliches erhält man, wenn man die Wahrscheinlichkeit vom roten und lila Feld bzw. die Wahrscheinlichkeit vom grünen und lila Feld vergleicht.
Bei einem Laplace-Experiment sind alle Ergebnisse gleich wahrscheinlich.
8
Beschreibe ein Zufallsexperiment, das kein Laplace-Experiment ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Die folgende Lösung ist eine mögliche Lösung. Du hast weitere Ideen? Schreib sie uns doch in die Kommentare!
Ein Glücksrad hat 5 Sektoren (Felder).
Diese sind jedoch unterschiedlich groß. Deshalb ist es zum Beispiel wahrscheinlicher, eine 5 zu drehen als eine 1.
Es handelt sich also nicht um ein Laplace-Experiment.
Damit es sich um ein Zufallsexperiment handelt, muss es die folgenden Bedingungen erfüllen:
Es muss mehr als ein mögliches Ergebnis geben und alle möglichen Ergebnisse müssen bekannt sein (sonst kein Zufallsexperiment)
Es darf nicht klar sein, welches Ergebnis eintreten wird (sonst kein Zufallsexperiment)
Wenn es jetzt zugleich kein Laplace-Experiment sein soll, dürfen die einzelnen Ergebnisse nicht alle gleich wahrscheinlich sein.
9
Gib für folgende Zufallsexperimente jeweils einen Ergebnisraum an und entscheide, ob es sich um ein Laplace-Experiment handelt:
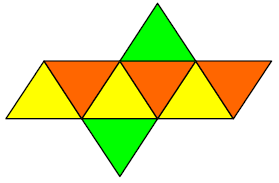
1. Ein aus dem abgebildeten Netz gebastelter „Würfel“ wird geworfen und die oben liegende Farbe wird notiert.
  Das ist ein Laplace-Experiment.
  Das ist kein Laplace-Experiment.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Es gibt drei Elementarereignisse, Grün, Gelb und Orange. Deren Wahrscheinlichkeit ist jeweils die Anzahl der entsprechend gefärbten Würfelseiten durch die Gesamtzahl der Würfelseiten.
  $\mathrm{Grün}\colon\;\,\dfrac28=\dfrac14=25\,\%\\\mathrm{Gelb}\colon\dfrac38=37{,}5\,\%\\\mathrm{Orange}\colon\;\dfrac38=37{,}5\,\%$
  $\Rightarrow$ Kein Laplace-Experiment, da die Elementarereignisse unterschiedlich wahrscheinlich sind.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
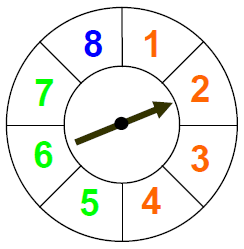
2. Das abgebildete Glücksrad wird gedreht und die angezeigte Zahl wird betrachtet.
  Das abgebildete Glücksrad wird gedreht und die angezeigte Farbe wird betrachtet.
  1 ist ein Laplace-Experiment.
  1 ist kein Laplace-Experiment.
  2 ist ein Laplace-Experiment.
  2 ist kein Laplace-Experiment.
  
  Laplace-Experiment
  Teilaufgabe 1
  Es gibt acht Elementarereignisse, die Zahlen von 1 bis 8. Die Wahrscheinlichkeit für das Eintreten eines Ereignisses ist gleich die Anzahl der entsprechenden Felder geteilt durch die Gesamtzahl der Felder.
  Da hier jede Zahl einem Feld entspricht, haben sie alle die Wahrscheinlichkeit $\frac{1}{8}$ .
  Insbesondere sind alle gleichwahrscheinlich, es handelt sich also um ein Laplace-Experiment.
  Teilaufgabe 2
  Hier gibt es drei Elementarereignisse, Orange, Grün und Blau. Diese haben jeweils die Wahrscheinlichkeit gleich der Anzahl der entsprechend farbigen Felder geteilt durch die Gesamtzahl der Felder:
  Orange: $\dfrac48=\dfrac12=50\,\%$
  Grün: $\dfrac38=37{,}5\,\%$
  Blau: $\dfrac18=12{,}5\,\%$
  $\Rightarrow$ Kein Laplace-Experiment, da die Elementarereignisse nicht gleichwahrscheinlich sind.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Aus einer Tüte mit 13 roten, 9 grünen, 12 gelben und 21 weißen Gummibärchen wird zufällig ein Gummibärchen ausgewählt.
  Das ist ein Laplace-Experiment.
  Das ist kein Laplace-Experiment
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Es gibt vier Elementarereignisse, Rot, Grün, Gelb und Weiß. Diese haben alle die Wahrscheinlichkeit gleich der Anzahl der jeweiligen Gummibärchen geteilt durch die Gesamtzahl der Gummibärchen. Berechne also erst die Gesamtzahl und dann die Wahrscheinlichkeiten:
  $13+9+12+21=55$
  Gesamtmenge ist Summe der verschiedenen Gummibärchen
  Rot: $\dfrac{13}{55}=23{,}6\,\%$
  Grün: $\dfrac9{55}=16{,}4\,\%$
  Gelb: $\dfrac{12}{55}=21{,}8\,\%$
  Weiß: $\dfrac{21}{55}=38{,}2\,\%$
  $\Rightarrow$ Es handelt sich nicht um ein Laplace-Experiment, da die Wahrscheinlichkeiten ungleich sind.
  Bemerkung: Die Rechnung ist nicht unbedingt nötig, schon aus der unterschiedlichen Anzahl der Gummibärchen ergibt sich, dass die Wahrscheinlichkeiten nicht gleich sein können.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10
Das Zufallsexperiment sei ein Würfelwurf und das Ereignis B="eine ungerade Augenanzahl wird gewürfelt". Gib $P(B)$ an.
$P(B)=\frac12$
$P(B)=\frac23$
$P(B)=\frac13$
$P(B)=\frac63$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Es ist
$\def\arraystretch{1.25} \begin{array}{l}B=\{1{,}3,5\}\;\;\;\;\;\;\;\;\;\;\;\;\,\Rightarrow\;\;\left|B\right|=3\\\Omega=\{1{,}2,3{,}4,5{,}6\}\;\;\Rightarrow\;\;\left|\Omega\right|=6\end{array}$
und somit
11
Aus einem Bridge-Spiel (52 Karten) wird eine Karte gezogen. Berechne die Wahrscheinlichkeit folgender Ereignisse:
1. A: ="Die gezogene Karte ist eine Pikkarte"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13\;$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{im}\;\mathrm{Spiel}\;\mathrm{vorhandenen}\;\mathrm{Pikkarten}\;}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{13}{52}=\frac14=0{,}25=25\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. B: ="Die gezogene Karte ist eine Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{im}\;\mathrm{Spiel}\;\mathrm{vorhandenen}\;\text{Damen}\;}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{4}{52}=\frac{1}{13}\approx0{,}0769\approx7{,}7\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. C: ="Die gezogene Karte ist Pik-Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik-Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikdamen}=1$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{im}\;\mathrm{Spiel}\;\mathrm{vorhandenen}\;\mathrm{Pik}\text{damen}\;}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{1}{52}\approx0{,}0192=1{,}92\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. D: ="Die gezogene Karte ist eine Pikkarte oder eine Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik oder Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13$
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  Eine der vier Damen ist aber gleichzeitig Pik, darf also nicht doppelt gezählt werden.
  $\Rightarrow \text{Kartenzahl}=13+4-1=16$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}$
  $=\frac{16}{52}\approx0{,}3077\approx30{,}8\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. F: ="Die gezogene Karte ist eine Pikkarte, aber keine Dame"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Pik aber keine Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13\;$
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikdamen}=1$
  Fasse das zur Anzahl der Karten zusammen.
  $\Rightarrow \text{Kartenzahl}=13-1=12$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{12}{52}=\frac3{13}=0{,}2308=23{,}1\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. G: ="Die gezogene Karte ist eine Dame, aber keine Pikkarte"
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist Dame aber nicht Pik", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikdamen}=1$
  Fasse das zur Kartenzahl zusammen.
  $\Rightarrow \text{Kartenzahl}=4-1=3$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac3{52}=0{,}058=5{,}8\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. H: ="Die gezogene Karte ist weder Pik noch Dame".
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Hier muss das Ereignis "gezogene Karte ist weder Pik noch Dame", bestimme also die Anzahl der entsprechenden Karten, um die Wahrscheinlichkeit berechnen zu können.
  $\mathrm{Anzahl}\;\mathrm{der}\;\mathrm{Pikkarten}=52:4=13\;$
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Damen}=4$
  $\mathrm{Anzahl}\;\mathrm{der}\;\text{Pikdamen}=1$
  Die Kartenzahl ist die Gesamtzahl abzüglich der Pik- und Damen-Karten. Dabei muss aber noch die Pikdame addiert werden, da diese doppelt abgezogen wird.
  $\Rightarrow \text{Kartenzahl}=52-13-4+1=36$
  Bereche die Wahrscheinlichkeit.
  $P=\frac{\text{Kartenzahl}}{\mathrm{Anzahl}\;\mathrm{aller}\;\mathrm{Spielkarten}\;}\;$
  $=\frac{36}{52}=\frac{9}{13}\approx0{,}692=69{,}2\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
12
Eine natürliche Zahl x mit $20<x\le30$ wird willkürlich gezogen. Wie groß ist die Wahrscheinlichkeit, dass
1. eine Primzahl gezogen wird
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und A="x ist Primzahl".
  $A=\left\{23{,}29\right\}\;\;\Rightarrow\;\;\left|A\right|=2$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne nun die Wahrscheinlichkeit.
  $P\left(A\right)=\frac2{10}=0{,}2=20\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 20% ist die gezogene Zahl eine Primzahl.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. eine gerade Zahl gezogen wird
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und B="x ist gerade".
  $B=\left\{22{,}24{,}26{,}28{,}30\right\}\;\;\Rightarrow\;\;\left|B\right|=5$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne die Wahrscheinlichkeit.
  $P\left(B\right)=\frac5{10}=0{,}50=50\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 50% ist die gezogene Zahl eine gerade Zahl.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. eine durch 4 teilbare Zahl gezogen wird
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und C="x ist durch 4 teilbar".
  $C=\left\{24{,}28\right\}\;\;\Rightarrow\;\;\left|C\right|=2$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne die Wahrscheinlichkeit.
  $P\left(E\right)=\frac2{10}=0{,}2=20\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 20% ist die gezogene Zahl durch 4 teilbar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. eine durch 4 und gleichzeitig durch 6 teilbare Zahl gezogen wird?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  Benutze die Formel zur Berechnung von Laplace-Wahrscheinlichkeiten, da alle Zahlen gleich wahrscheinlich sind.
  Bestimme also die Mächtigkeiten der Mengen $\Omega$ und D="x ist durch 4 und durch 6 teilbar".
  $D=\left\{24\right\}\;\;\Rightarrow\;\;\left|D\right|=1$
  $\Omega=\left\{21{,}22{,}23{,}24{,}25{,}26{,}27{,}28{,}29{,}30\right\}\;\;\Rightarrow\;\;\left|\Omega\right|=10$
  Berechne die Wahrscheinlichkeit.
  $P\left(D\right)=\frac1{10}=0{,}1=10\%$
  $\;\;\Rightarrow\;\;$ Mit einer Wahrscheinlichkeit von 10% ist die gezogene Zahl durch 4 und 6 teilbar.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
13
Die Oberfläche eines Würfels wird blau eingefärbt.
Dann wird der Würfel durch 6 parallel zur Würfeloberfläche verlaufende Schnitte in 27 kongruente Teilwürfel zerlegt.
Wie groß ist die Wahrscheinlichkeit dafür, dass ein willkürlich herausgegriffener Teilwürfel
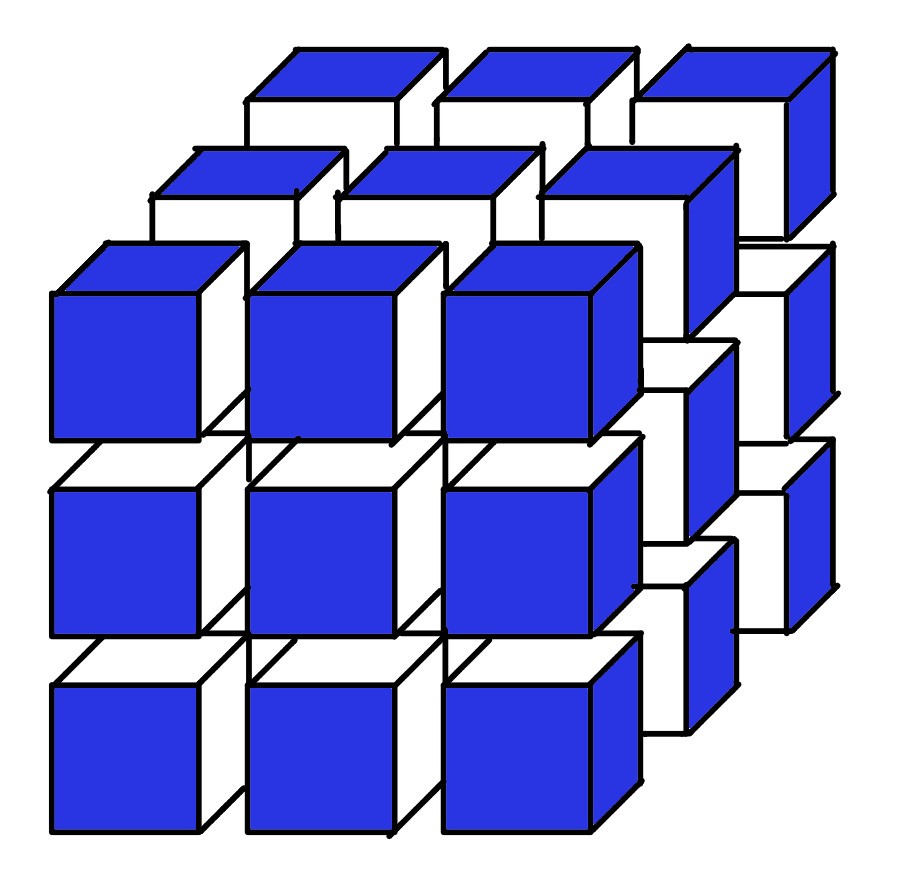
1. keine blaue Fläche hat. Gib die Antwort als Dezmalzahl ein.
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $\left|\mathrm{E}\right|=1$
  $\left|\mathrm{\Omega}\right|=27$
  $\mathrm P\left(\mathrm E\right)=\frac1{27}=3{,}7\%$
  $\Rightarrow$ Zu 3,7% zieht man einen Teil, dass keine blauen Flächen hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. genau zwei blaue Flächen hat? Gib die Antwort als Dezimalzahl ein
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
  $\left|\mathrm E\right|=12$
  $\left|\mathrm\Omega\right|=27$
  $\mathrm P\left(\mathrm E\right)=\frac{12}{27}=44{,}4\%$
  $\Rightarrow$ Man zieht zu 44,4% ein Würfelteil, das zwei eingefärbte Seiten hat.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
14
In einem Hörsaal sitzen 150 Studenten. 110 von ihnen sprechen nur Englisch, 20 nur Spanisch und 15 sprechen beide Sprachen.
1. Wie groß ist die relative Häufigkeit der Studenten, die mindestens eine der beiden Sprachen sprechen?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
  Bilde die Summe der Studenten, die Englisch und/oder Spanisch sprechen, geteilt durch die Gesamtanzahl der Studenten.
  Relative Häufigkeit:
  $\frac{110+20+15}{150}=\frac{145}{150}\approx\mathbf{96}{\boldsymbol,}\mathbf7\,\boldsymbol\%$
  Also sprechen ungefähr 96,7 % der Studenten mindestens eine der beiden Sprachen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie groß ist die relative Häufigkeit der Studenten, die keine der beiden Sprachen sprechen?
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenereignis
  $1-\frac{110+20+15}{150}=1-\frac{145}{150}$
  Schreibe auf einen Bruch und wandle am Ende in Prozent um.
  $1-\frac{145}{150}=\frac{150-145}{150}=\frac{5}{150}=\frac{1}{30}\approx3{,}33\,\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bilde die Summe der Studenten, die Englisch und/oder Spanisch sprechen, teile sie durch die Gesamtanzahl der Studenten und ziehe das Ergebnis von 1 ab.
15
30 Würfe mit einem Würfel ergaben folgendes Ergebnis:
Augen
1
2
3
4
5
6
Anzahl
4
6
2
6
5
7
Überprüfe mit diesen Zahlen die 3. Eigenschaft von relativer Häufigkeit
$h_n(A \cup B) = h_n(A) + h_n(B) - h_n(A \cap B)$
durch Rechnen.
Benutze dazu diese Ereignisse:
$A$ : Die Menge der Würfe mit maximal 3 Augen.
$B$ : Die Menge der Würfe mit gerader Augenzahl.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
$A=\{1{,}2,3\}, B=\{2{,}4,6\}$
Bestimme die Mengen A und B aus dem Text.
$h_n(A\cup B)=\frac{H(A\cup B)} {30}=\frac{H(\{1{,}2,3{,}4,6\})} {30}=\frac{4+6+2+6+7} {30}=\frac{25} {30}$
Berechen die relative Häufigkeit von $A \cup B$ .
$h_n(A)=\frac{H(A)} {30}=\frac{H(\{1{,}2,3\})} {30}=\frac{4+6+2} {30}=\frac{12} {30}$
Berechen die relative Häufigkeit von A.
$h_n(B)=\frac{H(B)} {30}=\frac{H(\{2{,}4,6\})} {30}=\frac{6+6+7} {30}=\frac{19} {30}$
Berechen die relative Häufigkeit von B.
$h_n(A\cap B)=\frac{H(A\cap B)} {30}=\frac{H(\{2\})} {30}=\frac{6} {30}$
Berechen die relative Häufigkeit von $A \cap B$ .
$h_n(A \cup B) = h_n(A) + h_n(B) - h_n(A \cap B)$ $\Leftrightarrow\frac{25} {30}=\frac{12} {30}+\frac{19} {30}-\frac{6} {30}$ $\Leftrightarrow\frac{25} {30}=\frac{25} {30}$
Setze in die Formel ein.
Gleichheit bestätigt die Formel.
Überprüfen der 3ten Rechenregel vom Artikel "Relative Häufigkeit" anhand eines Beispiels

Augen	1	2	3	4	5	6
Anzahl	4	6	2	6	5	7

Gegeben: $P\left(E_1\right)=0{,}4$ ; $P\left(E_2\right)=0{,}7$ ; $P\left(E_1\cap E_2\right)=0{,}3$

Berechne:

$P\left({\overline E}_1\right)$

$P\left(E_1\cup E_2\right)$

$P\left(E_1\cap{\overline E}_2\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionssätze für Wahrscheinlichkeiten

Lösung mit einer Vierfeldertafel

Trage die gegebenen Infos in die Vierfeldertafel ein und vervollständige diese anschließend:

	$E_1$	$\overline{E_1}$
$E_2$	0,3	0,4	0,7
$\overline{E_2}$	0,1	0,2	0,3
	0,4	0,6	1

Fettgedruckte Zahlen: aus Aufgabenstellung

Die Wahrscheinlichkeit $P(E_1\cap \overline{E_2})$ ist in der 3. Zeile links:

$P(E_1\cap\overline{E_2})=0{,}1$

Lösung mit Mengenalgebra

Verwende

$\left(E_1\cap E_2\right)\cup\left(E_1\cap{\overline E}_2\right)=E_1$

und wende dann die Gesetze der Mengenalgebra an:

$\Rightarrow P\left(E_1\cap E_2\right)+P\left(E_1\cap{\overline E}_2\right)=P\left(E_1\right)$

Die gesuchte Wahrscheinlichkeit wird der Einfachheit halber $x$ genannt.

$\displaystyle P\left(E_1\cap\overline{E}_2\right)$	$=$	$\displaystyle x$
	↓	Wir setzen die gegebenen Werte ein.
$\displaystyle 0{,}3+x$	$=$	$\displaystyle 0{,}4$
	↓	Löse nach x auf.
$\displaystyle x$	$=$	$\displaystyle 0{,}1$

$\Rightarrow P\left(E_1\cap{\overline E}_2\right)=0{,}1$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$P\left(E_1\cup{\overline E}_2\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionssätze für Wahrscheinlichkeiten

Lösung mit einer Vierfeldertafel

Trage die gegebenen Infos in die Vierfeldertafel ein und vervollständige diese anschließend:

	$E_1$	$\overline{E_1}$
$E_2$	0,3	0,4	0,7
$\overline{E_2}$	0,1	0,2	0,3
	0,4	0,6	1

Fettgedruckte Zahlen: aus Aufgabenstellung

Die Wahrscheinlichkeit für $P(E_1\cup\overline{E_2})$ ergibt sich entweder mit dem Satz von Sylvester (siehe unten) oder durch Addition der entsprechenden Wahrscheinlichkeiten der Schnittmengen im Inneren der Vierfeldertafel (orange):

$\displaystyle P(E_1\cup\overline{E_2})$	$=$	$\displaystyle P(E_1\cap E_2)+P(E_1\cap\overline{E_2})+P(\overline{E_1}\cap\overline{E_2})$
	$=$	$\displaystyle 0{,}3+0{,}1+0{,}2$
	$=$	$\displaystyle 0{,}6$

Mengenoperationen

Berechne zunächst die Wahrscheinlichkeit $P\left(E_1\cap{\overline E}_2\right)$ .

$P\left(E_1\cap{\overline E}_2\right)=x$

Diese Wahrscheinlichkeit wird erneut $x$ genannt.

$P\left(E_1\cap E_2\right) + P\left(E_1\cap \overline{E_2}\right)=P\left(E_1\right)$

Setze die Werte ein und löse nach $x$ auf:

$0{,}3+x=0{,}4$

$x=0{,}1$

Nun kannst du mit der folgenden Formel, die gesuchte Wahrscheinlichkeit bestimmen:

$P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)$

$P\left(E_1\cup{\overline E}_2\right)=P\left(E_1\right)+P\left({\overline E}_2\right)-P\left(E_1\cap{\overline E}_2\right)$

Setze die entsprechenden Werte ein.

$P\left(E_1\cup{\overline E}_2\right)=0{,}4+\left(1-0{,}7\right)-0{,}1=0{,}6$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$P(\overline{E_2})$

Gegeben ist: $P(A)=\frac15$ ; $P(\overline B)=\frac13$ ; $P\left(A\cap B\right)=\frac16$

Berechne:

$P\left(A\cup B\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionssätze für Wahrscheinlichkeiten

Lösung mithilfe einer Vierfeldertafel

	$A$	$\overline{A}$
$B$	$\color{ff6600}{\frac{1}{6}}$	$\frac 1 2$	$\frac 2 3$
$\overline{B}$	$\frac 1 {30}$	$\frac 3 {10}$	$\color{ff6600}{\frac{1}{3}}$
	$\color{ff6600}{\frac{1}{5}}$	$\frac 4 5$	1

Zahlen in Orange sind aus der Aufgabenstellung bzw. fest in der Vierfeldertafel.

Addiere die entsprechenden Wahrscheinlichkeiten der Schnittmengen:

$\displaystyle P\left(A\cup B\right)$	$=$	$\displaystyle P\left(A\cap B\right)+P\left(A\cap\overline{B}\right)+P\left(\overline{A}\cap B\right)$
	$=$	$\displaystyle \frac{1}{6}+\frac{1}{2}+\frac{1}{30}$
	$=$	$\displaystyle \frac{21}{30}$
	$=$	$\displaystyle 0{,}7$

Lösung mithilfe von Additionssätzen

$P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)=$

Bilde das Gegenereignis $P(B)$ von $P(\overline B)=\frac13$ .

	$=$	$\displaystyle \frac{1}{5}+\left(1-\frac{1}{3}\right)-\frac{1}{6}$
	$=$	$\displaystyle \frac{1}{5}+\frac{2}{3}-\frac{1}{6}$
	↓	Addiere, indem du den Hauptnenner bildest und auf diesen erweiterst (Hauptnenner ist 30).
	$=$	$\displaystyle \frac{6}{30}+\frac{20}{30}-\frac{5}{30}$
	$=$	$\displaystyle \frac{21}{30}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$P\left(\overline A\cap\overline B\right)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionssätze für Wahrscheinlichkeiten

Vierfeldertafel

	$A$	$\overline{A}$
$B$	$\color{ff6600}{\frac{1}{6}}$	$\frac 1 2$	$\frac 2 3$
$\overline{B}$	$\frac 1 {30}$	$\frac 3 {10}$	$\color{ff6600}{\frac{1}{3}}$
	$\color{ff6600}{\frac{1}{5}}$	$\frac 4 5$	1

Zahlen in Orange sind aus der Aufgabenstellung bzw. fest in der Vierfeldertafel.

Die Wahrscheinlichkeiten von Schnittmengen kannst du direkt der Vierfeldertafel entnehmen.

$P(\overline{A}\cap\overline{B})=\frac 3{10}=0{,}3$

Additionssätze

$\displaystyle P\left(\overline{A}\cap\overline{B}\right)$	$=$
	↓	Wende das De-Morgan-Gesetz für Vereinigungsmengen an.
	$=$	$\displaystyle P\left(\overline{A\cup B}\right)$
	↓	Bilde das Gegenereignis.
	$=$	$\displaystyle 1-P\left(A\cup B\right)$	$\displaystyle P(A\cup B)=\frac{21}{30}\quad\quad \text{; siehe Teilaufgabe a)}$
	$=$	$\displaystyle \frac{9}{30}$
	$=$	$\displaystyle \frac{3}{10}=0{,}3$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

$P\left(\overline A\cup B\right)$

Beim Werfen von zwei Würfeln werden folgende Ereignisse definiert:

$A:={}$ „Die Augensumme ist gerade“

$B:={}$ „Der erste Würfel zeigt eine gerade Augenzahl“

Für die Wahrscheinlichkeiten gilt: $P(A)=P(B)=0{,}5$ ; $P(A\cap B)=0{,}25$ .

Berechne die Wahrscheinlichkeit von:

$E_1:$ „ $A$ und-oder $B$ treten ein“

$E_2:$ „entweder $A$ oder $B$ tritt ein“

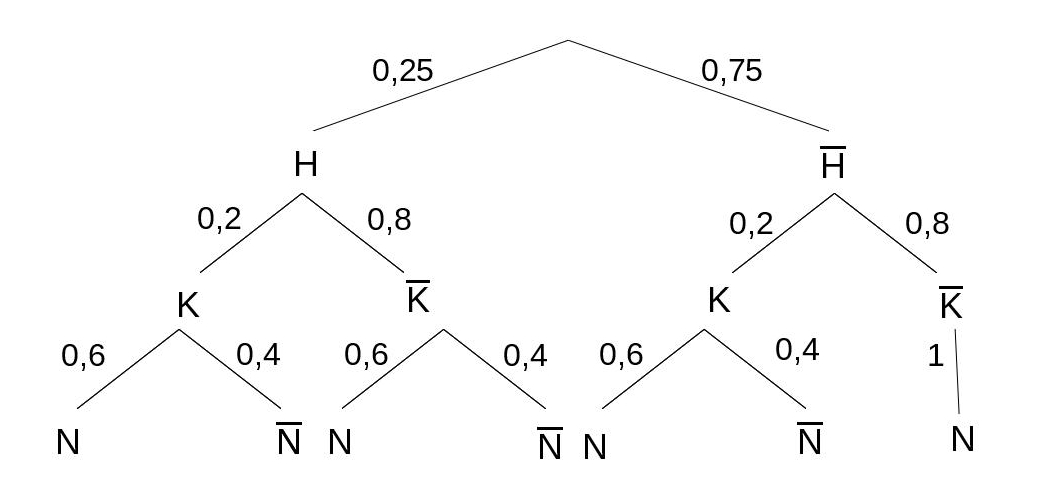
Die Glocken-Apotheke bietet ihren erkälteten Kunden Hustensaft (H), Kopfschmerztabletten (K) und Nasenspray (N) an, wobei jeder entsprechende Kunde mindestens eines dieser Produkte erwirbt. Im Folgenden werden nur diese drei Medikamente betrachtet.

Aus Erfahrung weiß der Apotheker, dass unabhängig voneinander 25% der Kunden einen Hustensaft erwerben und jeder fünfte Kunde Kopfschmerztabletten kauft. Kunden kaufen zu 60% auch ein Nasenspray, wenn sie mindestens eines der anderen Medikamente erwerben. Der Einkauf eines beliebig herausgegriffenen Kunden wird als Zufallsexperiment aufgefasst.

Erstellen Sie ein vollständiges Baumdiagramm und bestimmen Sie die Wahrscheinlichkeiten aller 7 Elementarereignisse. (5 BE)
[Teilergebnis: $P({H\overline{K}N})=0{,}12$ ]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregen
Mögliche Lösung für das Baumdiagramm:
Berechnung der Teilwahrscheinlichkeiten
Diese kannst du mithilfe der Pfadregeln berechnen:
$\def\arraystretch{1.25} \begin{array}{lll} P(HKN)&=0{,}25\cdot 0{,}2\cdot 0{,}6&=0{,}03\\P(HK\overline{N})&=0{,}25\cdot 0{,}2\cdot 0{,}4&=0{,}02\\P(H\overline{K}N)&=0{,}25\cdot 0{,}8\cdot 0{,}6&=0{,}12\\P(H\overline{K}\overline{N})&=0{,}25\cdot 0{,}8\cdot 0{,}4&=0{,}08\\P(\overline{H}KN)&=0{,}75\cdot 0{,}2\cdot 0{,}6&=0{,}09\\P(\overline{H}K\overline{N})&=0{,}75\cdot 0{,}2\cdot 0{,}4&=0{,}06\\P(\overline{H}\overline{K}N)&=0{,}75\cdot 0{,}8\cdot 1&=0{,}6\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Hinweise über die Reihenfolge des Baumdiagramms bekommst du sowohl im Text als auch aus dem Teilergebnis: Zuerst Hustensaft, dann Kopfschmerztabletten, dann Nasenspray.
Danach musst du den Ästen die richtigen Wahrscheinlichkeiten aus dem Text zuordnen.
Vergiss nicht am Ende die Wahrscheinlichkeiten aller Elementarereignisse mit den Pfadregeln zu berechnen.

Gegeben seien folgende Ereignisse:

$E_1$ : „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

$E_2$ : „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

$E_3=\overline{\overline{E_1} \cup E_2}$

Geben Sie diese Ereignisse in aufzählender Mengenschreibweise an. Beschreiben Sie $E_3$ möglichst einfach in Worten und berechnen Sie $P(E_3)$ . (5 BE)

$E_1$ : „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

Du bist also auf der Suche nach allen Ergebnissen, wo ein $\overline{K}$ vorkommt. Das ist bei folgenden Ergebnissen der Fall:

$E_1=\{H\overline{K}N; H\overline{K}\overline{N}; \overline{H}\overline{K}N\}$

$E_2$ : „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

Du bist also auf der Suche nach allen Ergebnissen, wo ein $N$ und $H$ , $K$ oder beides vorkommt. Das ist bei folgenden Ergebnissen der Fall:

$E_2=\{HKN; H\overline{K}N; \overline{H}KN\}$

$E_3=\overline{\overline{E_1} \cup E_2}$

Um es dir einfacher zu machen, kannst du hier die Regel von De Morgan anwenden, um $E_3$ umzuformen:

$E_3=\overline{\overline{E_1} \cup E_2}=E_1\cap \overline{E_2}$

Deswegen sucht du alle Ergebnisse, die gleichzeitig in Ereignis $E_1$ , aber nicht in Ereignis $E_2$ sind (es muss beides gleichzeitig stimmen, weil du die Schnittmenge suchst).

Das ist bei folgenden Ergebnissen der Fall:

$E_3=\{H\overline{K}\overline{N}; \overline{H}\overline{K}N\}$

Möglichst einfache Formulierung

Für eine möglichst einfache Formulierung schaust du dir am besten die beiden Ergebnisse genauer an. Vielleicht fällt dir dabei auf, dass in beiden Fällen zweimal ein "Nicht" vorkommt. Bei beiden Ergebnissen wird also genau ein Medikament eingekauft, beim ersten nur Hustensaft und beim zweiten nur Nasenspray. Eine mögliche Formulierung könnte deshalb lauten:

Es wird entweder nur Hustensaft oder nur Nasenspray gekauft.

Wahrscheinlichkeit von $E_3$

Die Wahrscheinlichkeit von $E_3$ kannst du nach den Pfadregeln berechnen. Unterschiedliche Pfade müssen dabei addiert werden:

$\displaystyle P\left(E_3\right)$	$=$	$\displaystyle P\left(\left\{H\overline{K}\overline{N}\right\}\right)+P\left(\left\{\overline{H}\overline{K}N\right\}\right)$
	↓	Nun kannst du die Wahrscheinlichkeiten aus Teilaufgabe 1.1 einsetzen.
	$=$	$\displaystyle 0{,}08+0{,}6$
	$=$	$\displaystyle 0{,}68$

Die Wahrscheinlichkeit für $E_3$ beträgt $68\%$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Apotheker bietet seinen Kunden nur Hustensaft der Marken A und B an. Von 500 Hustensaftkäufern entscheiden sich 400 für den Hustensaft A. Bei 280 der Kunden, die Hustensaft A kaufen, tritt eine Verbesserung der Symptome ein. Von den Käufern der Hustensaftmarke B geben 30 an, dass keine Verbesserung der Symptome auftritt.

Stellen Sie für den beschriebenen Sachverhalt eine vollständige Vierfeldertafel auf, überprüfen Sie, ob die Ereignisse
A: „Ein Kunde kauft Hustensaft der Marke A.“ und
V: „Es tritt eine Verbesserung der Symptome auf.“
stochastisch unabhängig sind und interpretieren Sie Ihr Ergebnis im Sinne der vorliegenden Thematik. (5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Vierfeldertafel
Du zeichnest zuerst eine leere Vierfeldertafel mit den beiden Ereignissen, die in der Aufgabenstellung angegeben sind. Anschließend kannst du die schwarzen Werte aus dem Text entnehmen und schließlich die roten Werte über Additionen und Subtraktionen ausrechnen, wie das genau funktioniert, wird im Artikel zu Vierfeldertafeln erklärt.
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \mathrm{A} & \mathrm{\overline A} & \ \\\hline\mathrm{V} & 280 & \color{red}{70} & \color{red}{350} \\\hline\mathrm{\overline V}& \color{red}{120} & 30 & \color{red}{150} \\\hline\ & 400 & \color{red}{100} & 500 \end{array}$
Nun kannst du eine Vierfeldertafel mit den zugehörigen Wahrscheinlichkeiten erstellen, indem du den Wert in jeder Zelle durch die Gesamtzahl $500$ teilst. Vielleicht hast du auch direkt diese Vierfeldertafel erstellt:
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \mathrm{A} & \mathrm{\overline A} & \ \\\hline\mathrm{V} & 0{,}56 & 0{,}14& 0{,}7\\\hline\mathrm{\overline V}& 0{,}24& 0{,}06 & 0{,}3 \\\hline\ & 0{,}8 & 0{,}2 & 1 \end{array}$
Stochastische Unabhängigkeit
Um zu überprüfen, ob zwei Ereignisse stochastisch unabhängig sind, musst du folgende Formel nachrechnen. Stimmt sie (auf beiden Seiten erhältst du dasselbe Ergebnis), dann sind sie unabhängig.
$P(A\cup V)=P(A)\cdot P(V)$
$P(A\cup V)$ kannst du in der Vierfeldertafel ablesen: $P(A\cup V)=0{,}56$
Auch die Werte für $P(A)$ und $P(V)$ kannst du ablesen und danach kannst du das Produkt ausrechnen:
$P(A)\cdot P(V)=0{,}8\cdot 0{,}7=0{,}56$
Damit stimmt die Formel und die beiden Ereignisse sind stochastisch unabhängig.
Bedeutung im Sachzusammenhang
Die Verbesserung der Symptome hängt nicht von der Wahl des Medikaments ab. Sie ist bei Hustensaft A genauso gut wie bei Hustensaft B.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechnen Sie $P(\overline{A}\cup V)$ . (2 BE)

21
1.0 Im Folgenden werden relative Häufigkeiten als Wahrscheinlichkeiten interpretiert.

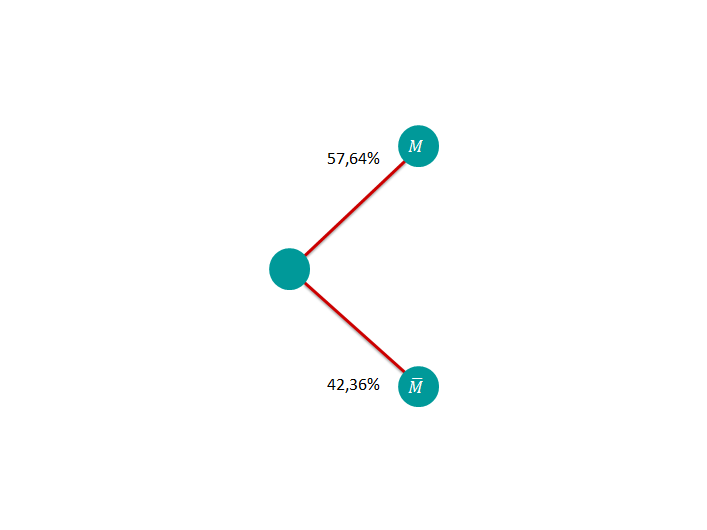
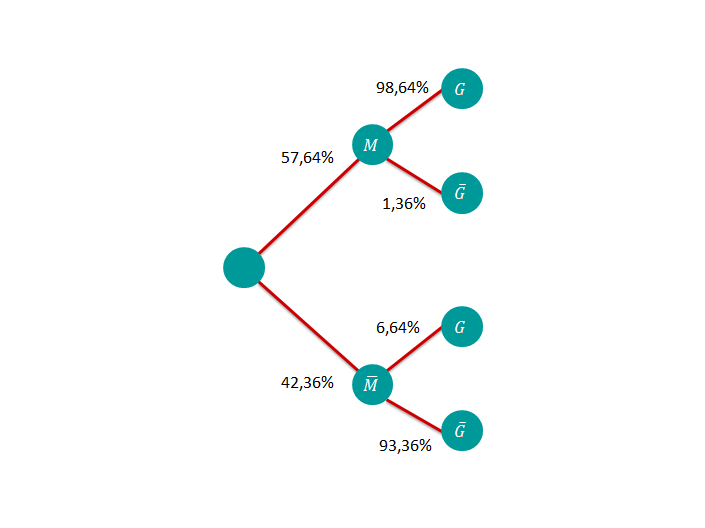
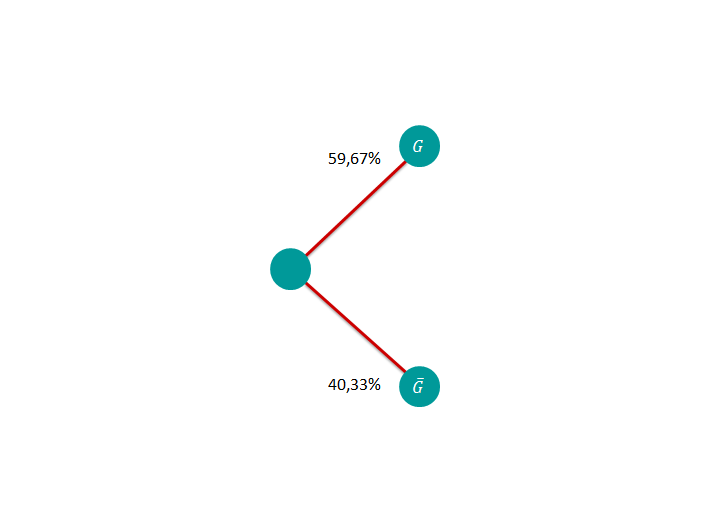
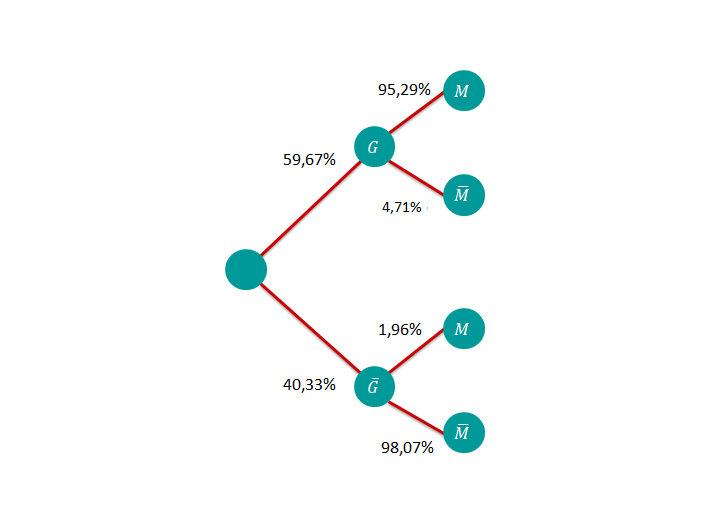
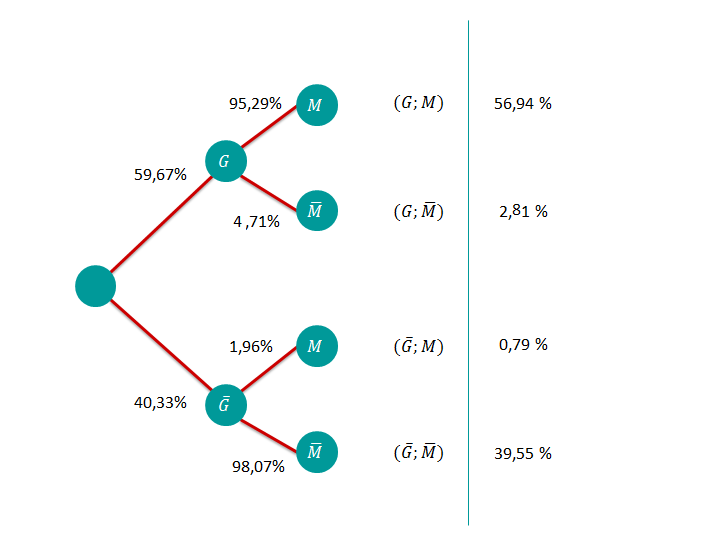
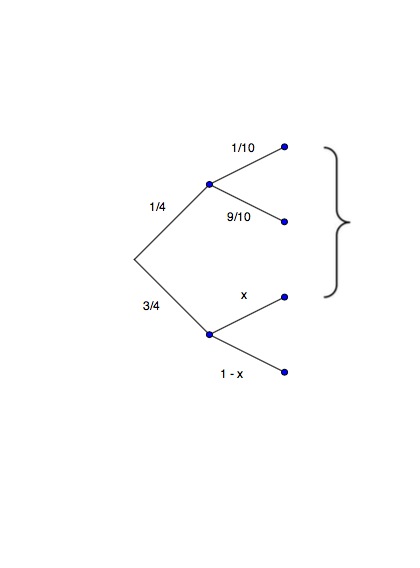
Die Fluggesellschaft TransAir bietet ihren Fluggästen neben den Standardmenüs $(S)$ auch vegetarische Menüs $(\overline{S)}$ an. Es werden nun die Fluggäste betrachtet, die tatsächlich essen und trinken. Diese Passagiere entscheiden sich zu 80% für den Menütyp $S$ und von diesen wählen 75% Fleisch $(F)$ , der Rest Fisch $(\overline F)$ . Von denen, die den Menütyp $S$ bevorzugen, entscheidet sich ein Fünftel für vegane Kost $(V)$ , der Rest für nicht vegane Kost $(\overline{V)}$ . Alle Fluggäste haben ferner die Wahlmöglichkeit zwischen einem alkoholischen Getränk $(A)$ und einem alkoholfreien Getränk $(\overline{A)}$ . Wählt ein Fluggast ein Standardmenü, so entscheidet er sich zu 50% für ein alkoholisches Getränk, ansonsten nur zu 25%. Die Entscheidung eines zufällig ausgewählten Passagiers für Menütyp, Speise und Getränk wird als Zufallsexperiment aufgefasst.
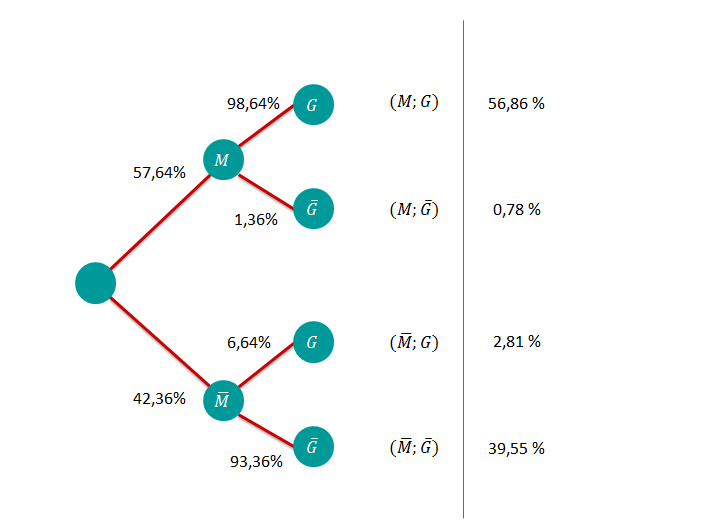
1.1 Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller acht Elementarereignisse dieses Zufallsexperiments.
1.2.0 Gegeben seien folgende Ereignisse:

$E_1$ : „Ein Fluggast entscheidet sich für ein alkoholfreies Getränk.“

$E_2=\{SFA;SF\overline A;\overline SVA;\overline SV\overline{A\}}$
1.2.1 Geben Sie $E_!$ in aufzählender Mengenschreibweise an und fassen Sie $E_2$ möglichst einfach in Worte. Prüfen Sie ferner $E_1$ und $E_2$ auf stochastische Unabhängigkeit.
1.2.2. Berechnen Sie die Wahrscheinlichkeit $P(E_1\cup E_2)$ .
1.2.3 Analysieren Sie den Fehler in der Rechnung $P(E_2)=\frac48=0{,}5$ .
22
Herr Huber hat eine Alarmanlage in seinem Auto installiert. Es werden die Ereignisse A: „Alarmanlage springt an“ und K: „Jemand versucht, das Auto aufzubrechen“ betrachtet. Beschreiben Sie folgende bedingte Wahrscheinlichkeiten mit Worten: $P_K\left(\overline{A}\right),\;P_{\overline K}\left(A\right),\;P_K\left(A\right),\;P_A\left(K\right)$ .
Welche dieser bedingten Wahrscheinlichkeiten sollten hoch bzw. niedrig sein?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
$P_K\left(\overline A\right)$ : Die Wahrscheinlichkeit, dass die Alarmanlage nicht anspringt unter der Bedingung, jemand versucht das Auto aufzubrechen.
Die Wahrscheinlichkeit sollte niedrig sein.
$P_{\overline K}\left(A\right)$ : Die Wahrscheinlichkeit, dass die Alarmanlage anspringt unter der Bedingung, niemand versucht das Auto aufzubrechen.
Die Wahrscheinlichkeit sollte ebenfalls niedrig sein.
$P_K\left(A\right)$ : Die Wahrscheinlichkeit, dass die Alarmanlage anspringt unter der Bedingung, jemand versucht das Auto aufzubrechen.
Die Wahrscheinlichkeit sollte hoch sein.
$P_A\left(K\right)$ : Die Wahrscheinlichkeit, dass jemand versucht das Auto aufzubrechen unter der Bedingung, die Alarmanlage springt an.
Dies wäre nicht sehr klug.

In einer Gruppe von 900 Personen haben sich 600 prophylaktisch gegen Grippe impfen lassen. Nach einer bestimmten Zeit wurde jedes Gruppenmitglied danach befragt, wer an einer Grippe erkrankte. Die Ergebnisse werden in einer 4-Feldtafel dargestellt.

Gruppe	$B\text{(erkrankt)}$	$\overline {B}\text{(gesund)}$	Summe
$A\text{(geimpft)}$	$60$	$540$	$600$
$\overline{A}\text{(ungeimpft)}$	$120$	$180$	$300$
Summe	$180$	$720$	$900$

Das Ereignis A sei "Person ist geimpft" und das Ereignis B: "Person erkrankt".

Berechnen Sie:

$P(A)$ , $P(B)$ , $P(A \cap B)$ , $P_A(B)$ , $P_B(A)$ sowie $P( \overline A$ $\cap B)$ und $P_{\overline{A}}(B)\$ .

Geben Sie die Bedeutung der einzelnen Ergebnisse in Textform an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeitsrechnung

Man berechnet nun nacheinander die gesuchten Wahrscheinlichkeiten. Einige kannst du auch direkt aus der Vierfeldertafel ablesen.

$P(A)$ gibt die Wahrscheinlichkeit an, mit der eine Person geimpft ist. Aus der Angabe kannst du ablesen, dass das 600 der 900 Personen sind (1. Zeile, rechts).

$\displaystyle P(A) = \frac{600} {900} = \frac{2} {3}$

$P(B)$ gibt die Wahrscheinlichkeit an, mit der eine Person erkrankt ist. Aus der Vierfeldertafel kannst du ablesen, dass es insgesamt 180 erkrankte Personen sind (1 Spalte, unten).

$\displaystyle P(B) = \frac{180} {900} = \frac{1} {5}$

$P(A \cap B)$ beschreibt die Wahrscheinlichkeit, mit der eine Person geimpft und krank ist. Aus der Vierfeldertafel kannst du ablesen, dass dies auf 60 Personen zutrifft (1 Zeile, 1 Spalte).

$\displaystyle P(A \cap B) = \frac{60} {900} = \frac{1} {15}$

$P_A(B)$ beschreibt die Wahrscheinlichkeit, dass eine Person an Grippe erkrankt, obwohl sie geimpft ist. Es geht also darum, wie groß der Anteil unter den Geimpften ist, die trotzdem erkrankt sind. Das sind $60$ von $600$ Geimpften

$P_A(B) = \dfrac{60}{600} = \dfrac{1}{10}$

Alternativ kannst du auch die Definition der bedingten Wahrscheinlichkeit benutzen: $P_A(B) = \dfrac{P(A \cap B)} {P(A)} = \dfrac{\frac{1} {15} } {\frac{2} {3}} = \frac{1} {10}$

$P_B(A)$ gibt die Wahrscheinlichkeit an, mit der eine Person geimpft ist, wenn man weiß dass sie erkrankt ist. Mit der Definition der bedingten Wahrscheinlichkeit erhältst du:

$P_B(A)= \frac{P(A \cap B)} {P(B)}$ $\displaystyle = \frac{\frac{1} {15} } {\frac{1} {5}} = \frac{1} {3}$

$P(\overline A \cap B)$ gibt die Wahrscheinlichkeit an, dass eine Person nicht geimpft wurde und krank ist. Du kannst anhand der Vierfeldertafel ablesen (1 Spalte, 2 Zeile), dass es davon 120 Personen gibt.

$\displaystyle P(\overline A \cap B) = \dfrac{120}{900}=\dfrac2{15}$

$P_{\overline{A}} (B)$ gibt die Wahrscheinlichkeit an, mit der eine zuvor nicht geimpfte Person krank ist. Von den $300$ nicht geimpften Personen sind $120$ erkrankt. Also ist die gesuchte Wahrscheinlichkeit:

$P_{\overline{A}} (B)$ $\displaystyle =\frac{120}{300}=\frac25$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

In einem Großversuch wurde ein Medikament getestet. Die Ergebnisse sind in einer Tabelle festgehalten. Dabei bedeuten:

$M$ : Medikament genommen
$\overline M$ : Placebo genommen
$G$ : Gesund geworden
$\overline G$ : nicht gesund geworden

	$G$	$\overline G$	Summe
$M$	$6312$	$87$	$6399$
$\overline M$	$312$	$4390$	$4702$
Summe	$6624$	$4477$	$11101$

Stelle die relativen Häufigkeiten in einer Vierfeldertafel dar und stelle die dazugehörigen Baumdiagramme auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel

Erstellen der Vierfeldertafel:

	$G$	$\overline G$	Summe
$M$	$\frac{6312}{11101}\\=0{,}5686$	$\frac{87}{11101}\\=0{,}0078$	$\frac{6399}{11101}\\=0{,}5764$
$\overline M$	$\frac{312}{11101}\\=0{,}0281$	$\frac{4390}{11101}\\=0{,}3955$	$\frac{4702}{11101}\\=0{,}4236$
Summe	$\frac{6624}{11101}\\=0{,}5967$	$\frac{4477}{11101}\\=0{,}4033$	$1$

Erstellen des 1. Baumdiagramms:

Die erste Spalte des Baumdiagramms kannst du in der Vierfeldertafel ablesen.

Die Pfadwahrscheinlichkeiten in der zweiten Spalte kannst du mithilfe der Formel für bedingte Wahrscheinlichkeit ausrechnen:

Genauso kannst du jetzt die Wahrscheinlichkeiten für $P(\overline G\vert M);P(\overline M \vert G);P(\overline M \vert\overline G)$ ausrechnen.

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

Nun kannst du das Baumdiagramm vervollständigen. Dazu musst du nur noch mithilfe der 1. Pfadregel die jeweiligen Wahrscheinlichkeiten ausrechnen

Erstellen des 2. Baumdiagramms:

Die erste Spalte des Baumdiagramms kannst du in der Vierfelder Tafel ablesen.

Die Pfadwahrscheinlichkeiten in der zweiten Spalte kannst du mithilfe der Formel für bedingte Wahrscheinlichkeit ausrechnen:

Genauso kannst du jetzt die Wahrscheinlichkeiten für $P(\overline M \vert G);P(\overline G \vert M);P(\overline M \vert\overline G)$ ausrechnen.

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

Nun kannst du das Baumdiagramm vervollständigen. Dazu musst du nur noch mithilfe der 1. Pfadregel die jeweiligen Wahrscheinlichkeiten ausrechnen

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Medikament eingenommen hat, zu genesen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Zuerst überlegt man, was für eine Wahrscheinlichkeit gesucht ist.
Man sucht die Wahrscheinlichkeit, dass eine Person genesen wird, unter der Bedingung, dass sie das Medikament eingenommen hat.
Das ist die Wahscheinlichkeit $P(G\vert M)$ .
Verwende die Definition der bedingten Wahrscheinlichkeit und ließ die Werte aus der Vierfeldertafel ab:
Alternativlösung
Da in Teilaufgabe a) schon das Baumdiagramm gezeichnet wurde, lässt sich aus diesem auch ganz einfach $\displaystyle P(G\vert M)$ ablesen. Du findest den Wert in der zweiten Ebene am obersten Zweig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Placebo eingenommen hat, nicht zu genesen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Zuerst überlegt man sich, welche Wahrscheinlichkeit gesucht ist. Hier sucht man diejenige Wahrscheinlichkeit, mit der eine Person, von der man weiß, dass sie einen Placebo genommen hat, nicht gesund geworden ist.
Das ist $P_{\overline{M}} \overline G$ .
Verwende die Definition der bedingten Wahrscheinlichkeit und ließ dann die Werte aus der Vierfeldertafel ab.
Alternativlösung
In Teilaufgabe a) wurde schon das Baumdiagramm erstellt. Hieraus lässt sich $P_{\overline{M}} \overline G$ ablesen. Man findet den Wert in der zweiten Ebene, der unterste Zweig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

25
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
An einem Berufskolleg werden alle 674 Schüler/innen befragt, ob sie rauchen oder nicht rauchen. Das Ergebnis der Befragung sieht wie folgt aus: 82 der insgesamt 293 Schüler (männlich) gaben an zu rauchen. 250 Schülerinnen gaben an, nicht zu rauchen.
1. Stellen Sie den Sachzusammenhang in einer 4-Feldtafel dar. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
  A: Die Person ist männlich.
  B: Die Person ist Raucher
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldtafel
  Stelle für die Ereignisse $A$ und $B$ sowie die Gegenereignisse $\overline{A}$ und $\overline B$ eine Vierfeldtafel auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & & & \\\hline\mathrm{\overline B} & & & \\\hline\ & & & \end{array}$
  Trage die Informationen aus der Aufgabenstellung in die Vierfeldtafel ein.
  $A \cap B$ : 82
  $A$ : 293
  $\overline A \cap \overline B$ : 250
  Gesamtanzahl Schüler/innen: 674
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & & \\\hline\mathrm{\overline B} & & 250 & \\\hline\ & 293 & & 674\end{array}$
  Ergänze die fehlenden Informationen und trage sie in die Vierfeldtafel ein.
  $A \cap \overline B$ : 293 - 82 = 211
  $\overline{A}$ : 674 - 293 = 381
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & & \\\hline\mathrm{\overline B} & 211 & 250 & \\\hline\ & 293 & 381 & 674\end{array}$
  Ergänze die restlichen fehlenden Informationen und trage sie in die Vierfeldtafel ein.
  $\overline A \cap B$ : 381 - 250 = 131
  $\overline B$ : 211 + 250 = 461
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Ergänze die letzte Spalte $B$ . Prüfe, ob das Gleiche herauskommt, wenn du von der Gesamtanzahl $\overline B$ abziehst und wenn du $B \cap A$ und $B \cap \overline A$ addierst.
  $B$ : 674 - 461 = 213
  $B$ : 82 + 131 = 213
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person weiblich und Nichtraucherin?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit aus relativer Häufigkeit
  Ereignis definieren
  Die gesuchten Eigenschaften sind die Kombination Ereignisse
  $\overline A$ : Person ist weiblich
  $\overline B$ : Person ist nicht Raucher(in)
  Suche also nach dem Ereignis $\overline A \cap \overline B$ .
  Lese relative Häufigkeit aus Vierfeldtafel ab
  Stelle eine Vierfeldtafel zur Aufgabe auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Lese die Anzahl der Ereignisse $\overline A \cap \overline B$ und die Gesamtanzahl von Ereignissen in der Tabelle ab.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & \mathbf{250} & 461 \\\hline\ & 293 & 381 & \mathbf{674}\end{array}$
  Berechne nun die relative Häufigkeit, indem du die Anzahl der Ereignisse $\overline A \cap \overline B$ durch die Gesamtanzahl von Ereignissen teilst.
  Ergebnis
  Die relative Häufigkeit der weiblichen Nichtraucherinnen gibt die Wahrscheinlichkeit an, mit der eine zufällig ausgewählte Person weiblich und Nichtraucherin ist.
  Sie beträgt 37 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Der Schulleiter sieht eine Schülerin im Aufenthaltsraum. Mit welcher Wahrscheinlichkeit ist diese Schülerin Nichtraucherin?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Es ist bereits bekannt, dass es sich bei der Person um eine Schülerin handelt. Das Ereignis $\overline A$ ist also bereits vorgegeben. Nun bestimme die Wahrscheinlichkeit, dass die Person nicht raucht ( $\overline B$ ), wenn bereits bekannt ist, dass die Person weiblich ist ( $\overline A$ ).
  Schreibe die Definition der bedingten Wahrscheinlichkeit $P_{\overline A} (\overline B)$ .
  Stelle die Vierfeldtafel zur Aufgabe auf
  Schreibe die befüllte Vierfeldtafel zur Aufgabenstellung auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Lese die Anzahl der Ereignisse $\overline A \cap \overline B$ , $\overline A$ und die Gesamtanzahl der Ereignisse ab, um die relativen Häufigkeiten zu bestimmen.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & \mathbf{250} & 461 \\\hline\ & 293 & \mathbf{381} & \mathbf{674}\end{array}$
  Gebe die Wahrscheinlichkeiten $P(\overline A \cap \overline B)$ und $P(\overline A)$ an.
  
  Berechne nun die bedingte Wahrscheinlichkeit
  Ergebnis
  Die Wahrscheinlichkeit, dass es sich bei der Schülerin um eine Raucherin handelt, ist 66 %.
  Beachte, dass hier etwas anderes gefragt wurde als bei der Frage "Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person weiblich und Nichtraucherin?".
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Untersuchen Sie, ob das Ereignis "männlich" und das Ereignis "Raucher" voneinander abhängige Ereignisse sind.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
  Prüfe Unabhängigkeit von Ereignissen
  Zwei Ereignisse $A$ und $B$ heißen stochastisch abhängig, wenn gilt: $P(A \cap B) \neq P(A) \cdot P(B).$
  Stelle Vierfeldtafel auf
  Erstelle eine Vierfeldtafel für die in der Aufgabenstellung beschriebene Situation.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Lese aus Vierfeldtafel die Anzahl der Ereignisse $A$ , $B$ , $A \cap B$ und die Gesamtanzahl der Ereignisse ab.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & \mathbf{82} & 131 & \mathbf{213} \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & \mathbf{293} & 381 & \mathbf{674}\end{array}$
  Gib die relativen Häufigkeiten und somit die Wahrscheinlichkeiten $P(A)$ , $P(B)$ und $P(A \cap B)$ an.
  Prüfe nun, ob die Ereignisse unabhängig sind.
  $P(A) \cdot P(B) = \frac{293 \cdot 213}{674^2} = \frac{62409}{454276} = 0{,}14$ $\neq 0{,}12 = P(A \cap B)$
  Ergebnis
  Die Ergebnisse "männlich" und "Raucher" sind stochastisch voneinander abhängig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

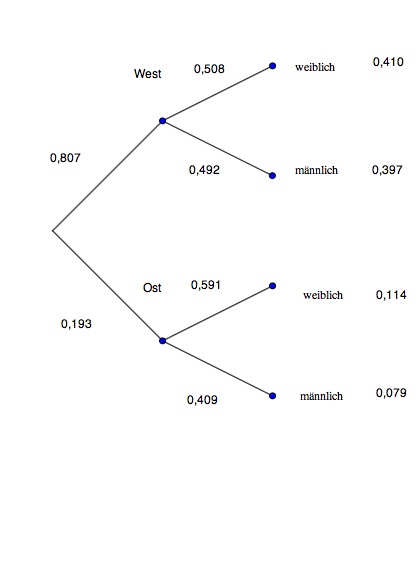
Mehr Abiturientinnen als Abiturienten:

52,4% der 244600 Jugendlichen, die am Ende des vergangenen Schuljahres ihre Schule mit der allgemeinen Hochschulreife verließen, waren Frauen. In den neuen Ländern und in Berlin liegt der Frauenanteil mit 59,1% deutlich höher als im früheren Bundesgebiet (50,8%).

Stellen Sie eine 4-Feldtafel auf, die diesen Sachzusammenhang beschreibt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: 4-Feldertafel

Stelle eine 4-Feldertafel auf

Definiere Ereignisse

Definiere die Ereignisse, die in der Aufgaben genannt wurden.

$A$ : Person kommt aus den alten Bundesländern (Westdeutschland)
$\overline A$ : Person kommt aus den neuen Bundesländern oder Berlin (Ostdeutschland)
$B$ : Person ist eine Frau
$\overline B$ : Person ist ein Mann

Berechne absolute Häufigkeiten

Berechne Anzahl der Ereignisse "Person ist weiblich".

$0{,}524 \cdot 244600 = 128170{,}4 \approx 128170$

Berechne Anzahl der Ereignisse "Person ist männlich".

$244600 - 128170 = 116430$

Definiere Anzahl der Absolventen aus dem Westen und aus dem Osten

$x$ : Anzahl der Absolventen West $244600-x$ : Anzahl der Absolventen Ost

Definiere Anzahl der weiblichen Absolventen aus jeweils Westen und Osten

$0{,}508 \cdot x$ : Anzahl der weiblichen Absolventen West

$0{,}591 \cdot (244600 - x)$ : Anzahl der weiblichen Absolventen West

Gib die Anzahl der weiblichen Absolventinnen als Summe der Absolventinnen aus Ost und West an.

$0{,}508 \cdot x + 0{,}591 \cdot (244600-x) = 128170$

Löse nach x auf und berechne so die Anzahl der Absolventen in Westdeutschland

$x = 197453$

Berechne damit jeweils die Anzahl der Absolventen und Absolventinnen in jeweils Ost und West.

	Zusammenfassung
weiblich West	$0{,}508 \cdot 197453 = 100306$
weiblich Ost	$128170 - 100306 = 27864$
männlich West	$197453 - 100306 = 97147$
männlich Ost	$116430 - 97147 = 19283$

Stelle eine Vierfeldertafel auf

Zeichne als erstes eine leere Vierfeldertafel.

$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & & & \\\hline\mathrm{\overline B} & & & \\\hline\ & & & \end{array}$

Trage die zuvor berechneten Informationen in die Vierfeldertafel ein.

$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & \\\hline\mathrm{\overline B} & 97147 & 19283 & \\\hline\ & & & 244600 \end{array}$

Ergänze die fehlenden Werte.

$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & 128170\\\hline\mathrm{\overline B} & 97147 & 19283 & 116430 \\\hline\ & 197453& 47147 &244600 \end{array}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Zeichnen Sie ein Baumdiagramm mit dem 1. Merkmal "Herkunft" (Ost, West) und dem 2. Merkmal "Geschlecht" (männlich, weiblich).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
Zeichne ein Baumdiagramm
Ermittle Wahrscheinlichkeiten
Schreibe die zum Zeichnen des Baumdiagramms benötigten Wahrscheinlichkeiten auf. Verwende dazu die Informationen aus der Vierfeldertafel aus der ersten Teilaufgabe.
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & 128170\\\hline\mathrm{\overline B} & 97147 & 19283 & 116430 \\\hline\ & 197453& 47147& 244600 \end{array}$
Berechne nun die benötigten relativen Häufigkeiten.
$P(A) = \frac{197453}{244600} = 0{,}807$
$P (\overline A) = \frac{47147}{244600} = 0{,}193$
$P(A \cap B) = \frac{100306}{244600} = 0{,}410$
$P(A \cap \overline B) = \frac{97147}{244600} = 0{,}397$
$P(\overline A \cap B) = \frac{27864}{244600} = 0{,}114$
$P(\overline A \cap B) = \frac{19283}{244600} = 0{,}079$
$P_{A} (B) = \frac{P(A \cap B)}{P(A)} = \frac{100306}{197453} = 0{,}508$
$P_{A} (\overline B) = \frac{P(A \cap \overline B)}{P(A)} = \frac{97147}{197453} = 0{,}492$
$P_{\overline A} (B) = \frac{P(\overline A \cap B)}{P(\overline A)} = \frac{27864}{47147} = 0{,}591$
$P_{\overline A} (\overline B) = \frac{P(\overline A \cap \overline B)}{P(\overline A)} = \frac{19283}{47147} = 0{,}409$
Zeichne das Baumdiagramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichnen Sie ein Baumdiagramm mit dem 1. Merkmal "Geschlecht" (männlich, weiblich) und dem 2. Merkmal "Herkunft" (Ost, West).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
Zeichne ein Baumdiagramm
Ermittle Wahrscheinlichkeiten
Schreibe die zum Zeichnen des Baumdiagramms benötigten Wahrscheinlichkeiten auf. Verwende dazu die Informationen aus der Vierfeldertafel aus der ersten Teilaufgabe.
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & 128170\\\hline\mathrm{\overline B} & 97147 & 19283 & 116430 \\\hline\ & 197453& 47147& 244600 \end{array}$
Berechne nun die benötigten relativen Häufigkeiten.
$P(B) = \frac{128170}{244600} = 0{,}524$
$P (\overline B) = \frac{116430}{244600} = 0{,}476$
$P(A \cap B) = \frac{100306}{244600} = 0{,}410$
$P(A \cap \overline B) = \frac{97147}{244600} = 0{,}397$
$P(\overline A \cap B) = \frac{27864}{244600} = 0{,}114$
$P(\overline A \cap B) = \frac{19283}{244600} = 0{,}079$
$P_{B} (A) = \frac{P(A \cap B)}{P(B)} = \frac{100306}{128170} = 0{,}783$
$P_{B} (\overline A) = \frac{P(\overline A \cap B)}{P(B)} = \frac{27864}{128170} = 0{,}217$
$P_{\overline B} (A) = \frac{P(A \cap \overline B)}{P(\overline B)} = \frac{97147}{116430} = 0{,}834$
$P_{\overline B} (\overline A) = \frac{P(\overline A \cap \overline B)}{P(\overline B)} = \frac{19283}{116430} = 0{,}166$
Zeichne das Baumdiagramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Aus der Gesamtheit aller Abiturientinnen und Abiturienten des betrachteten Jahrgangs wurde eine Person zufällig ausgewählt.
(1) Mit welcher Wahrscheinlichkeit stammt diese Person aus Ostdeutschland?
(2) Mit welcher Wahrscheinlichkeit ist die ausgewählte Person eine Frau?
(3) Falls diese Person aus Ostdeutschland kommt, mit welcher Wahrscheinlichkeit ist dies ein Mann?
(4) Falls diese Person eine Frau ist, mit welcher Wahrscheinlichkeit stammt sie aus Westdeutschland?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit berechnen
Teilaufgabe 1
Berechne die Wahrscheinlichkeit, dass diese Person aus Ostdeutschland stammt.
Die Wahrscheinlichkeit beträgt $P(\overline A) = \frac{47147}{244600} = 0{,}193$ .
Teilaufgabe 2
Berechne die Wahrscheinlichkeit, dass diese Person eine Frau ist.
Die Wahrscheinlichkeit beträgt $P(B) = \frac{128170}{244600} = 0{,}524$ .
Teilaufgabe 3
Berechne die Wahrscheinlichkeit mit der die Person ein Mann ist, wenn bekannt ist, dass sie aus Ostdeutschland kommt.
Die Wahrscheinlichkeit ist $P_{\overline A} (\overline B) = \frac{P(\overline A \cap \overline B)}{P(\overline A)} = \frac{19283}{47147} = 0{,}409$ .
Teilaufgabe 4
Berechne die Wahrscheinlichkeit mit der diese Person aus Westdeutschland stammt, wenn bekannt ist, dass sie eine Frau ist.
Die Wahrscheinlichkeit ist $P_B (A) = \frac{P(A \cap B)}{P(B)} = \frac{100306}{128170} = 0{,}783$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Gegeben sind Ereignisse A, B mit $P\left(A\right)=0{,}72$ , $P\left(A\cap B\right)=0{,}18$ , $P\left(A\cup B\right)=0{,}832$ . Wie groß sind dann die bedingten Wahrscheinlichkeiten $P_B\left(A\right)$ und $P_{\overline{A}}\left(B\right)$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit berechnen

Berechne die bedingte Wahrscheinlichkeit $P_B(A)$

Definition von bedingter Wahrscheinlichkeit

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

Lies die gegebenen Wahrscheinlichkeiten aus der Aufgabenstellung ab.

$P(A) = 0{,}72\\P(A\cap B)=0{,}18\\P(A \cup B) = 0{,}832$

Verwende den Additionssatz für Wahrscheinlichkeiten.

$\displaystyle P(A\cup B)$	$=$	$\displaystyle P(A) + P(B) - P(A\cap B)$
	↓	Berechne $P(B)$ , indem du den Additionssatz umstellst.
$\displaystyle P(B)$	$=$	$\displaystyle P(A \cup B) - P(A) + P(A\cap B)$
	↓	Setze die Werte ein.
$\displaystyle P(B)$	$=$	$\displaystyle 0{,}832 - 0{,}72 +0{,}18$
$\displaystyle P(B)$	$=$	$\displaystyle 0{,}292$

Berechne $P_B(A)$

$P_B(A) = \dfrac{0{,}18}{0{,}292}\approx 0{,}62$

Berechne die bedingte Wahrscheinlichkeit $P_{\overline{A}}(B)$

Verwende das Gesetz der totalen Wahrscheinlichkeit und stelle nach $P_{\overline{A}}(B)$ um.

$\displaystyle P(B)$	$=$	$\displaystyle P(A)\cdot P_A(B)\;+\;P(\overline A)\cdot P_{\overline A}(B)$	$\displaystyle -P(A)\cdot P_A(B)$
$\displaystyle P(B)-P(A)\cdot P_A(B)$	$=$	$\displaystyle P(\overline{A})\cdot P_{\overline{A}}(B)$	$\displaystyle :P(\overline{A})$
$\displaystyle \frac{P(B)-P(A)\cdot P_A(B)}{P(\overline{A})}$	$=$	$\displaystyle P_{\overline{A}}(B)$
	↓	Seiten vertauscht
$\displaystyle P_{\overline{A}}(B)$	$=$	$\displaystyle \frac{P(B)-P(A)\cdot P_A(B)}{P(\overline{A})}$

Berechne $P(\bar A)$ , die Wahrscheinlichkeit zum Gegenereignis von $A$ .

$P(\bar A) = 1 - P(A) = 1 - 0{,}72 = 0{,}28$

Berechne $P_A(B)$ .

$P_A(B) = \dfrac{P(A\cap B)}{P(A)} = \dfrac{0{,}18}{0{,}72} = 0{,}25$

Berechne $P_{\overline A}(B)$ , indem die Werte in die Gleichung eingesetzt werden.

$P_{\overline A}(B) = \dfrac{0{,}292-0{,}72\cdot 0{,}25}{0{,}28} = 0{,}4$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

28
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
(Aus dem Leistungskurs-Abitur Bayern 2008/IV) In einem Molkereibetrieb wird Fruchtjoghurt hergestellt und in Becher abgefüllt. In dem Betrieb werden täglich gleich viele Becher der Sorten Erdbeere, Kirsche, Heidelbeere und Ananas abgefüllt. Bei einer Tagesproduktion, bei der 4 % der Becher einen defekten Deckel aufweisen, fällt auf, dass unter den Erdbeerjoghurtbechern sogar jeder zehnte Deckel fehlerhaft ist.
1. Bestimmen Sie den Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten. Klären Sie, ob es durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt gelingen kann, den angestrebten Qualitätsstandard von insgesamt höchstens 1 % Ausschussanteil einzuhalten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimme bedingte Wahrscheinlichkeit
  Definiere Ereignisse
  Definiere zunächst die Ereignisse, die in der Aufgabenstellung beschrieben werden.
  Ereignis $A$ : In dem Becher ist Erdbeerjoghurt
  Ereignis $B$ : Der Becher hat einen defekten Deckel
  Definiere Wahrscheinlichkeiten
  Gebe aus der Aufgabenstellung jeweils die Wahrscheinlichkeit an, mit denen eins der zuvor definierten Ereignisse eintritt.
  $P(A) = \frac{1}{4} = 0{,}25$ $P(\overline A) = \frac{3}{4} = 0{,}75$
  In dem Betrieb werden täglich gleich viele Becher der Sorten Erdbeere, Kirsche, Heidelbeere und Ananas abgefüllt.
  $P(B) = 0{,}04$ $P(\overline B) = 0{,}96$
  Bei einer Tagesproduktion, bei der 4 % der Becher einen defekten Deckel aufweisen, …
  $P_A(B) = \frac{1}{10} = 0{,}1$ $P_A(\overline B) = \frac{9}{10} = 0{,}9$
  …, dass unter den Erdbeerjoghurtbechern sogar jeder zehnte Deckel fehlerhaft ist.
  Bestimme den Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten
  Bestimme die bedingte Wahrscheinlichkeit $P_{\overline A} (B)$ . Zeichne dazu ein Baumdiagramm mit den Ereignissen $A$ , $B$ , $\overline A$ und $\overline B$ .
  Schreibe die Wahrscheinlichkeit $P(B)$ als Summe aus $P_{A}(B)$ und $P_{\overline A}(B)$ .
  $P(B) = P_{A}(B) + P_{\overline A}(B)$
  Setze für die Wahrscheinlichkeiten die Werte aus dem Baumdiagramm ein.
  $0{,}04 = \frac{1}{4} \cdot \frac{1}{10} + \frac{3}{4} \cdot x$
  Löse nach $x$ auf.
  $x = 0{,}02$
  Ergebnis
  Der Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten, ist 2 %.
  Kläre, ob es durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt gelingen kann, höchstens 1% Ausschussanteil gesamt zu produzieren
  Es soll insgesamt höchstens 1% Ausschussanteil produziert werden. Es soll also gelten $P(B) \leq 0{,}01$ . Gebe den bestmöglichen Fall an, der durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt erreicht werden kann.
  $P_A (B) = 0$
  Das bestmögliche Ergebnis für die Erdbeerjoghurtbecher ist , wenn alle Erdbeerjoghurtbecher intakte Deckel haben.
  Schreibe die Wahrscheinlichkeit $P(B)$ wieder als Summe aus $P_{A}(B)$ und $P_{\overline A}(B)$ .
  $P(B) = P_{A}(B) + P_{\overline A}(B)$
  Setze die Werte für die Wahrscheinlichkeiten des bestmöglichen Falls mit ausschließlich intakten Erdbeerjoghurtdeckeln ein.
  $P(B) = \frac{1}{4} \cdot 0 + \frac{3}{4} \cdot 0{,}02 = 0{,}015$
  Prüfe, ob $P(B)$ kleiner als 0,01 ist.
  $0{,}015 > 0{,}01$
  Ergebnis
  Es ist nicht möglich, durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt höchstens 1% Ausschussanteil gesamt zu produzieren. Selbst beim Absenken des Ausschussanteils bei Erdbeer auf 0 % hätte insgesamt noch 1,5 % der produzierten Becher einen defekten Deckel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Alle Becher mit defektem Deckel dieser Tagesproduktion werden aussortiert. Mit welcher Wahrscheinlichkeit enthält ein Becher, der zufällig aus den verbleibenden Bechern ausgewählt wird, Erdbeerjoghurt?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimme bedingte Wahrscheinlichkeit
  Gesucht ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Becher Erdbeerjoghurt enthält ( $A$ ), wenn bekannt ist, dass dieser Becher einen intakten Deckel ( $\overline B$ ) hat.
  Schreibe als erstes die Definition der bedingten Wahrscheinlichkeit auf.
  Gebe die Wahrscheinlichkeit $P(\overline B)$ an.
  $P(\overline B) = 1 - 0{,}04 = 0{,}96$
  Gebe die Wahrscheinlichkeit $P(A \cap \overline B)$ an.
  Berechne die bedingte Wahrscheinlichkeit.
  Ergebnis
  Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Becher Erdbeerjoghurt enthält ( $A$ ), wenn bekannt ist, dass dieser Becher einen intakten Deckel ( $\overline B$ ) hat, beträgt 23,44 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
29
An Freitagen fehlen David und Clara oft in der Schule, und zwar David mit einer Wahrscheinlichkeit von 0,3 und Clara mit einer Wahrscheinlichkeit von 0,45. Die Wahrscheinlichkeit, dass beide anwesend sind, beträgt nur 0,4. Sind die Abwesenheit von David und Clara unabhängige Ereignisse?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
$P$ ("David nicht da") $= P\left(\overline D\right)=0{,}3$
Bestimme die Wahrscheinlichkeit für das Gegenereignis:
$\Rightarrow P\left(D\right)=1-0{,}3=0{,}7$
$P$ ("Clara nicht da") $= P\left(\overline C\right)=0{,}45$
Bestimme die Wahrscheinlichkeit für das Gegenereignis:
$\Rightarrow P\left(C\right)=1-0{,}45=0{,}55$
In der Aufgabe ist außerdem angegeben:
$P\left(D\cap C\right)=0{,}4$
Stelle die Formel für die stochastische Unabhängigkeit auf.
$P\left(D\cap C\right)=P\left(D\right)\cdot P\left(C\right)$
Setze die oben bestimmten Werte ein.
$0{,}4\overset?=0{,}7\cdot0{,}55$
Multipliziere.
$0{,}4\neq0{,}385$
$\Rightarrow$ Die Abwesenheiten der beiden Schüler sind stochastisch abhängig.
30
Bei einem Preisausschreiben gibt es 6 Gewinner, auf die 3 Laptops und 3 Fernseher verteilt werden sollen. Dies soll durch das Werfen einer Münze geschehen, wobei Kopf einem Fernseher und Zahl einem Laptop entspricht. Nacheinander wird für die Gewinner geworfen, bis keine Auswahlmöglichkeit mehr besteht, da nur noch entweder Laptops oder Fernseher verfügbar sind.
1. Hat nach diesem System jeder Gewinner die gleichen Chancen auf einen Laptop?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Wir werden zeigen, dass wirklich jeder Gewinner die gleichen Chancen auf einen Laptop hat. Dazu betrachten wir die Wahrscheinlichkeiten für jeden Gewinner einzeln.
  Die Wahrscheinlichkeit für einen Laptop bei Gewinner 1, 2 und 3:
  Bei den Gewinnern 1, 2 und 3 können Laptops und Fernseher noch nicht ausgegegangen sein und der Münzwurf bestimmt den Preis.
  Wir gehen natürlich von einer Laplacemünze aus mit der Wahrscheinlichkeit für Kopf von $\frac12$ .
  Laplace Münzwurf.
  $\Rightarrow$ P(Gewinner 1 gewinnt Laptop) = P(Gewinner 2 gewinnt Laptop) = P(Gewinner 3 gewinnt Laptop) = $\frac12$
  Die Wahrscheinlichkeit für einen Laptop bei Gewinner 4:
  Für Gewinner 4 gibt es jetzt aber schon mehrere Möglichkeiten. Es kann sein, dass für ihn noch eine Münze geworfen wird, es kann aber auch sein, dass Fernseher oder Laptops bereits nicht mehr verfügbar sind.
  Fallunterscheidung anhand der bisherigen Ergebnisse.
  Möglichkeit 1: Es sind sowohl Laptops als auch noch Fernseher vorhanden:
  P(Gewinner 4 gewinnt Laptop) = $\frac12$
  Betrachte den Fall, dass bereits alle Laptops verteilt wurden. Damit ist ein Laptop als Gewinn sicher ausgeschlossen.
  Möglichkeit 2: Alle Laptops wurden bereits verteilt:
  P(Gewinner 4 gewinnt Laptop) = 0
  Betrachte den Fall, dass bereits alle Fernseher verteilt wurden. Damit ist ein Laptop sicher.
  Möglichkeit 3: Alle Fernseher wurden bereits verteilt
  P(Gewinner 4 gewinnt Laptop) = 1
  Um die Gesamtwahrscheinlichkeit zu bestimmen, müssen wir nun die einzelnen Wahrscheinlichkeiten mit ihrer Eintrittswahrscheinlichkeit multiplizieren und dann addieren.
  Berechne die Wahrscheinlichkeit, dass alle Laptops bereits verteilt wurden.
  P(Alle Laptops wurden bereits verteilt) = P(3 mal Zahl bei drei Münzwurfen)
  Laplace Münzwurf.
  zu Möglichkeit 2:
  P(3 mal Zahl bei drei Münzwurfen) = $\frac12\cdot\frac12\cdot\frac12=\frac18$
  Berechne die Wahrscheinlichkeit, dass alle Fernseher bereits verteilt wurden.
  P(Alle Fernseher wurden bereits verteilt) = P(3 mal Kopf bei drei Münzwurfen)
  zu Möglichkeit 3:
  P(3 mal Kopf bei drei Münzwurfen) = $\frac12\cdot\frac12\cdot\frac12=\frac18$
  Die restliche Wahrscheinlichkeit ergibt sich als 1 abzüglich der Wahrscheinlichkeit, dass alle Laptops verteilt sind und abzüglich der Wahrscheinlichkeit, dass alle Fernseher verteilt sind.
  zu Möglichkeit 1:
  P(Es wird noch eine Münze geworfen) = P(Es sind weder alle Laptops verteilt noch alle Fernseher) = 1 - P(Alle Laptops verteilt) - P(Alle Fernseher verteilt) = $1-\frac18-\frac18=\frac34$
  Berechne anhand dieser Ergebnisse die Wahrscheinlichkeit, dass Gewinner 4 einen Laptop gewinnt.
  P(Gewinner 4 gewinnt Laptop) = $\frac34\cdot\frac12\;+\;\frac18\;\cdot\;0+\;\frac18\;\cdot\;1\;=\;\frac12$
  Wie man im Beispiel von Gewinner 4 sehen kann, ist es gleichwahrscheinlich, ob bereits alle Laptops oder alle Fernseher verteilt wurden. Das eine Ereignis impliziert eine 0%ige Chance, das andere eine 100%ige. Auch beim 5. oder 6. Gewinner, ist es gleichwahrscheinlich, ob alle Fernseher oder alle Laptops bereits verteilt wurden. Das liegt daran, dass bei einer Münze Kopf und Zahl gleich wahrscheinlich sind.
  Nehmen wir an, die Wahrscheinlichkeit, dass alle Laptops verteilt sind sei beim 5. Gewinner gleich A.
  Dann ist die Gewinnwahrscheinlichkeit für Gewinner 5:
  $\mathrm{P(Gewinner \;5 \;gewinnt \;Laptop)}=\underbrace{\mathrm{P(Es \;sind \;noch \;Laptops \;und \;Fernseher \;verfügbar)}}_{1-A-A}\cdot\underbrace{\mathrm{P( Münzwurf)}}_{\frac12}+\underbrace{\mathrm{P(Alle \;Laptops \;sind \;verteilt)}}_{A}\cdot0 + \mathrm{P(Alle \;Fernseher \;sind \;verteilt)}\cdot1$
  $=\left(1-\mathrm A-\mathrm A\right)\frac12+\mathrm A\;=\;\frac12-\mathrm A+\mathrm A=\frac12$ .
  Das Gleiche gilt für Gewinner 6. Die Wahrscheinlichkeit ist also für alle Fälle immer $\frac12$ .
  Alle Gewinner haben somit die gleichen Chancen auf einen Laptop.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ist es für je zwei der Gewinner gleichwahrscheinlich, einen Fernseher zu erhalten?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
  Diese Aufgabe kann analog zu Teilaufgabe a) beantwortet werden, indem man die Begriffe Fernseher und Laptop vertauscht.
  Man kann auch argumentieren, dass durch den Münzwurf der Erhalt eines Laptops und Fernsehers exakt gleich wahrscheinlich sind. Da auch für jeden Gewinner der Erhalt eines Laptops gleich wahrscheinlich ist (Wahrscheinlichkeit 0,5), muss umgekehrt auch für jeden Gewinner der Erhalt eines Fernsehers gleich wahrscheinlich sein (Wahrscheinlichkeit 1-0,5 = 0,5).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
31
Herr Müller kommt im Durchschnitt an 8 von 100 Tagen zu spät zur Arbeit. Zu seiner Arbeitsstätte fährt er manchmal mit dem eigenen Auto, an 60% aller Arbeitstage nimmt er jedoch öffentliche Verkehrsmittel. Er hat beobachtet, dass er durchschnittlich in 5% aller Fälle mit dem Auto unterwegs ist und zu spät zur Arbeit kommt.
Sind das Zu-Spät-Kommen und die Nutzung des eigenen Autos voneinander stochastisch unabhängig?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfeldertafel
Gerne können Sie Ihre Lösungen mit uns teilen!
Erstelle eine Vierfeldertafel - daraus kannst du leicht die benötigten Wahrscheinlichkeiten erhalten.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle P\left(\left\{\omega_1;\omega_2\right\}\right)$	$=$	$\displaystyle P\left(\left\{\omega_1\right\}\right)+P\left(\left\{\omega_2\right\}\right)$
	↓	Ersetze $P(\{\omega_1\})=2\cdot P(\{\omega_2\})$ und $P(\{\omega_1;\omega_2\})=0{,}2$
$\displaystyle 0{,}2$	$=$	$\displaystyle 2\cdot P\left(\left\{\omega_2\right\}\right)+P\left(\left\{\omega_2\right\}\right)$
	↓	Fasse zusammen
$\displaystyle 0{,}2$	$=$	$\displaystyle 3\cdot P\left(\left\{\omega_2\right\}\right)$	$\displaystyle :3$
$\displaystyle P\left(\left\{\omega_2\right\}\right)$	$=$	$\displaystyle \frac{1}{15}$

$\displaystyle P\left(\overline{E}_1\right)+P\left(E_1\right)$	$=$	$\displaystyle 1$	$\displaystyle -P\left(E_1\right)$
$\displaystyle P\left(\overline{E}_1\right)$	$=$	$\displaystyle 1-P\left(E_1\right)$
	↓	Für $P\left(E_1\right)$ 0,4 einsetzen.
	$=$	$\displaystyle 1-0{,}4$
	$=$	$\displaystyle 0{,}6$

$\displaystyle P\left(E_1\cup E_2\right)$	$=$	$\displaystyle P\left(E_1\right)+P(E_2)-P\left(E_1\cap E_2\right)$
$\displaystyle$	$=$	$\displaystyle 0{,}4+0{,}7-0{,}3$
	$=$	$\displaystyle 0{,}8$

$\displaystyle P\left(\overline{E_2}\right)+P\left(E_2\right)$	$=$	$\displaystyle 1$	$\displaystyle -P\left(E_2\right)$
$\displaystyle P\left(\overline{E}_2\right)$	$=$	$\displaystyle 1-P\left(E_2\right)$
	↓	Für $P\left(E_2\right)$ den Wert 0,7 einsetzen.
$\displaystyle$	$=$	$\displaystyle 1-0{,}7$
	$=$	$\displaystyle 0{,}3$

$\displaystyle P\left(E_2\right)$	$=$	$\displaystyle P(A\cup B)-P(A\cap B)$
	↓	Wahrscheinlichkeit für $P(A\cup B)$ wurde in Teilaufgabe a) berechnet.
	$=$	$\displaystyle 0{,}75-0{,}25$
	$=$	$\displaystyle 0{,}5$

$\displaystyle x$	$=$	$\displaystyle 1-\dfrac{3}{4}$
	↓	nach x auflösen
$\displaystyle x$	$=$	$\displaystyle \dfrac14=0{,}25=25\,\%$

$\displaystyle P\left(\overline{A}\cup B\right)$	$=$
	↓	Verwende die Formel $P(A \cup B)=P(A) + P(B) - P(A \cap B)$ .
	$=$	$\displaystyle P\left(\overline{A}\right)+P\left(B\right)-P\left(\overline{A}\cap B\right)$
	↓	Ziehe vom Ereignis $B$ das Ereignis, dass $B$ eintritt und $A$ nicht eintritt, ab, so erhältst du das Ereignis, dass $B$ und $A$ eintreten.
	$=$	$\displaystyle P\left(\overline{A}\right)+P\left(A\cap B\right)$
	$=$	$\displaystyle 1-P\left(A\right)+P\left(A\cap B\right)$
	$=$	$\displaystyle 1-\frac{1}{5}+\frac{1}{6}$
	↓	Zum Subtrahieren bilde den Hauptnenner und erweitere auf diesen (hier Hauptnenner 30)
	$=$	$\displaystyle 1-\frac{6}{30}+\frac{5}{30}$
	$=$	$\displaystyle 1-\frac{1}{30}$
	$=$	$\displaystyle \frac{29}{30}$

$\displaystyle P\left(E_1\right)$	$=$	$\displaystyle P(A\cup B)$
	↓	Stelle die Wahrscheinlichkeit für $P(A\cup B)$ auf. Verwende den Satz von Sylvester.
$\displaystyle P(A\cup B)$	$=$	$\displaystyle P(A)+P(B)-P(A\cap B)$
	↓	Setze die gegebenen Werte ein.
	$=$	$\displaystyle 0{,}5+0{,}5-0{,}25$
	$=$	$\displaystyle 0{,}75$

$\displaystyle P(\overline{A}\cup V)$	$=$	$\displaystyle P(\overline{A})+P(V)-P(\overline{A}\cap V)$
	↓	Lies die Wahrscheinlichkeiten in der Vierfeldertafel ab.
	$=$	$\displaystyle 0{,}2+0{,}7-0{,}14$
	$=$	$\displaystyle 0{,}76$
	$=$	$\displaystyle 76\%$

Übungsaufgaben 2. SA 11 Stochastik

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung durch eine Gleichung

Darstellung in der Vierfeldertafel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Werfen eines Würfels, der mit den Zahlen 1,2,3,4,5,21{,}2,3{,}4,5{,}21,2,3,4,5,2 versehen ist.

Werfen einer Münze

Werfen eines Würfels mit den Zahlen 1,3,5,7,9,111{,}3,5{,}7,9{,}111,3,5,7,9,11 versehen.

Ziehen einer Karte aus einem Kartenspiel mit 52 Karten

Ziehen einer Kugel aus einer Urne mit 10 Kugeln

Ziehen einer Kugel aus einer Urne mit 6 weißen und 4 schwarzen Kugeln

Zufallsexperiment 1

Zufallsexperiment 2

Zufallsexperiment 3

Hast du eine Frage oder Feedback?

Teilaufgabe 1

Teilaufgabe 2

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung mit einer Vierfeldertafel

Lösung mit Mengenalgebra

Hast du eine Frage oder Feedback?

Lösung mit einer Vierfeldertafel

Mengenoperationen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung mithilfe einer Vierfeldertafel

Lösung mithilfe von Additionssätzen

Hast du eine Frage oder Feedback?

Vierfeldertafel

Additionssätze

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung der Teilwahrscheinlichkeiten

Hast du eine Frage oder Feedback?

E1E_1E1​: „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

E2E_2E2​: „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

E3=E1‾∪E2‾E_3=\overline{\overline{E_1} \cup E_2}E3​=E1​​∪E2​​

Möglichst einfache Formulierung

Wahrscheinlichkeit von E3E_3E3​

Hast du eine Frage oder Feedback?

Vierfeldertafel

Stochastische Unabhängigkeit

Bedeutung im Sachzusammenhang

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Erstellen der Vierfeldertafel:

Erstellen des 1. Baumdiagramms:

Erstellen des 2. Baumdiagramms:

Hast du eine Frage oder Feedback?

Alternativlösung

Hast du eine Frage oder Feedback?

Alternativlösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Werfen eines Würfels, der mit den Zahlen $1{,}2,3{,}4,5{,}2$ versehen ist.

Werfen eines Würfels mit den Zahlen $1{,}3,5{,}7,9{,}11$ versehen.

$E_1$ : „Ein zufällig ausgewählter Kunde kauft keine Kopfschmerztabletten.“

$E_2$ : „Es wird Nasenspray und mindestens ein weiteres Produkt gekauft.“

$E_3=\overline{\overline{E_1} \cup E_2}$

Wahrscheinlichkeit von $E_3$

Berechne die bedingte Wahrscheinlichkeit $P_B(A)$

Berechne die bedingte Wahrscheinlichkeit $P_{\overline{A}}(B)$