Aufgaben zum Thema bedingte Wahrscheinlichkeit

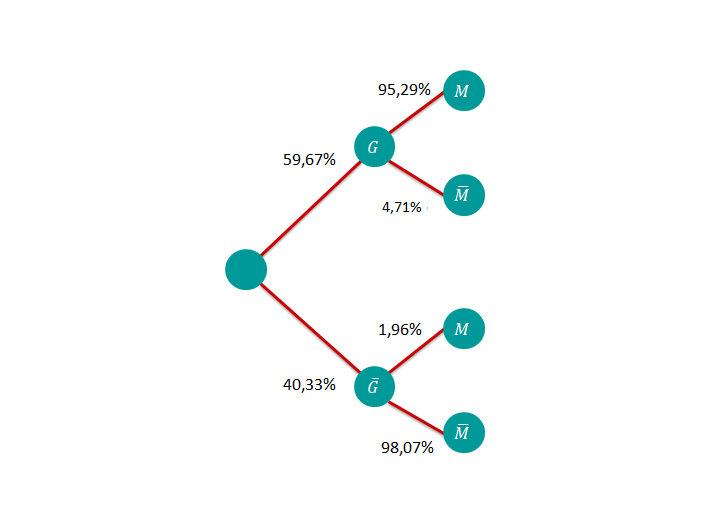
In einem Großversuch wurde ein Medikament getestet. Die Ergebnisse sind in einer Tabelle festgehalten. Dabei bedeuten:

$M$ : Medikament genommen
$M$ : Placebo genommen
$G$ : Gesund geworden
$G$ : nicht gesund geworden

	$G$	$G$	Summe
$M$	$6312$	$87$	$6399$
$M$	$312$	$4390$	$4702$
Summe	$6624$	$4477$	$11101$

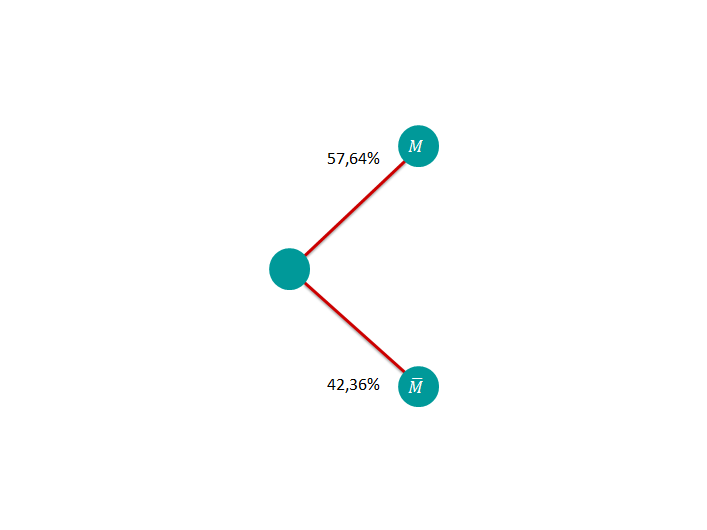
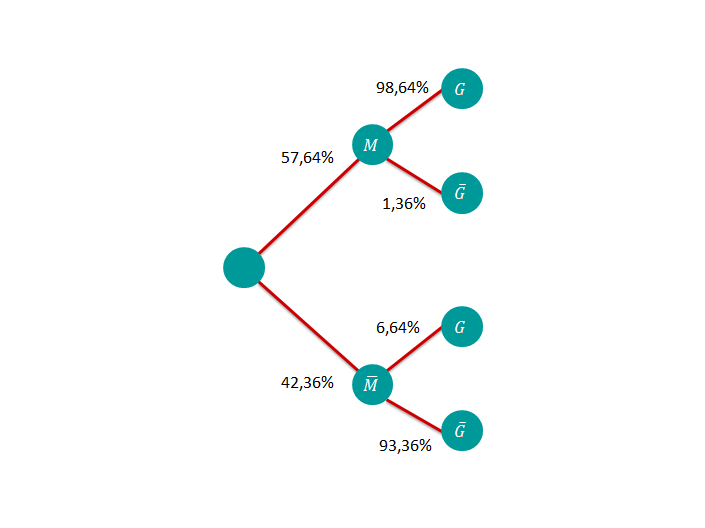
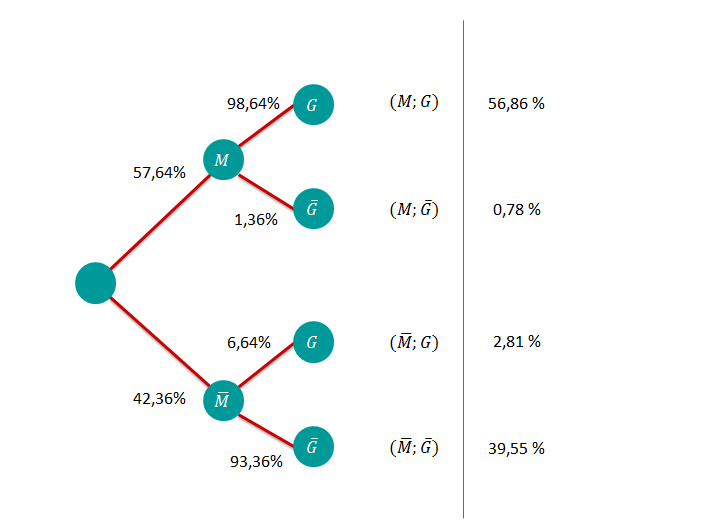
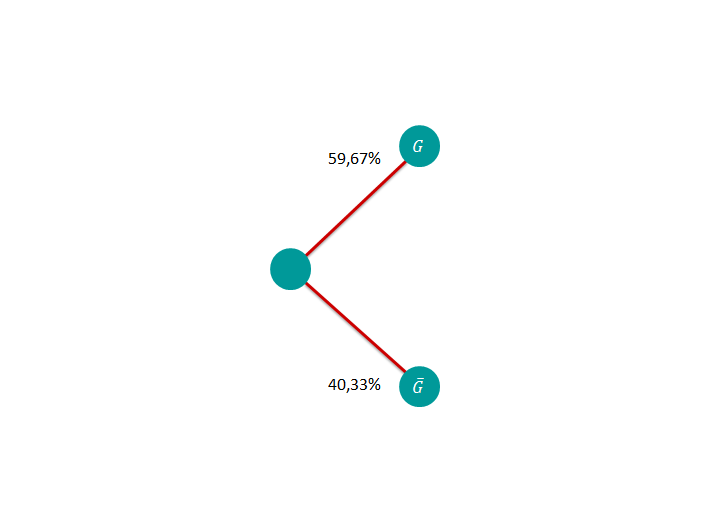
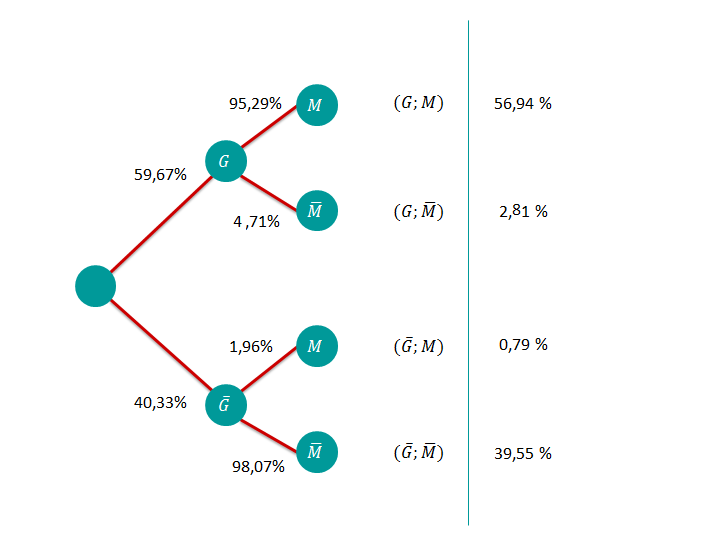
Stelle die relativen Häufigkeiten in einer Vierfeldertafel dar und stelle die dazugehörigen Baumdiagramme auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Erstellen der Vierfeldertafel:
$G$
$G$
Summe
$M$
$\begin{array}{l} \frac{6312}{11101} \\ = 0,5686 \end{array}$
$\begin{array}{l} \frac{87}{11101} \\ = 0,0078 \end{array}$
$\begin{array}{l} \frac{6399}{11101} \\ = 0,5764 \end{array}$
$M$
$\begin{array}{l} \frac{312}{11101} \\ = 0,0281 \end{array}$
$\begin{array}{l} \frac{4390}{11101} \\ = 0,3955 \end{array}$
$\begin{array}{l} \frac{4702}{11101} \\ = 0,4236 \end{array}$
Summe
$\begin{array}{l} \frac{6624}{11101} \\ = 0,5967 \end{array}$
$\begin{array}{l} \frac{4477}{11101} \\ = 0,4033 \end{array}$
$1$
Erstellen des 1. Baumdiagramms:
Die erste Spalte des Baumdiagramms kannst du in der Vierfeldertafel ablesen.
Die Pfadwahrscheinlichkeiten in der zweiten Spalte kannst du mithilfe der Formel für bedingte Wahrscheinlichkeit ausrechnen:
Genauso kannst du jetzt die Wahrscheinlichkeiten für $P (G | M); P (G | M); P (G | M)$ ausrechnen.
$P (G | M) = \frac{P (M \cap G)}{P (M)} \approx \frac{0,78 %}{57,64 %} \approx 0,0136 \approx 1,36 %$
$P (G | M) = \frac{P (M \cap G)}{P (M)} \approx \frac{2,81 %}{42,36 %} \approx 0,0664 \approx 6,64 %$
$P (G | M) = \frac{P (M \cap G)}{P (M)} \approx \frac{39,55 %}{42,36 %} \approx 0,9336 \approx 93,36 %$
Nun kannst du das Baumdiagramm vervollständigen. Dazu musst du nur noch mithilfe der 1. Pfadregel die jeweiligen Wahrscheinlichkeiten ausrechnen
Erstellen des 2. Baumdiagramms:
Die erste Spalte des Baumdiagramms kannst du in der Vierfelder Tafel ablesen.
Die Pfadwahrscheinlichkeiten in der zweiten Spalte kannst du mithilfe der Formel für bedingte Wahrscheinlichkeit ausrechnen:
Genauso kannst du jetzt die Wahrscheinlichkeiten für $P (M | G); P (M | G); P (M | G) |$ ausrechnen.
$P (M | G) \approx \frac{P (G \cap M)}{P (G)} \approx \frac{2,81 %}{59,67 %} \approx 0,0471 \approx 4,71 %$
$P (M | G) \approx \frac{P (G \cap M)}{P (G)} \approx \frac{0,78 %}{40,33 %} \approx 0,0196 \approx 1,96 %$
$P (M | G) \approx \frac{P (G \cap M)}{P (G)} \approx \frac{39,55 %}{40,33 %} \approx 0,9807 \approx 98,07 %$
Nun kannst du das Baumdiagramm vervollständigen. Dazu musst du nur noch mithilfe der 1. Pfadregel die jeweiligen Wahrscheinlichkeiten ausrechnen
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Medikament eingenommen hat, zu genesen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Zuerst überlegt man, was für eine Wahrscheinlichkeit gesucht ist.
Man sucht die Wahrscheinlichkeit, dass eine Person genesen wird, unter der Bedingung, dass sie das Medikament eingenommen hat.
Das ist die Wahscheinlichkeit $P (G | M)$ .
Verwende die Definition der bedingten Wahrscheinlichkeit und ließ die Werte aus der Vierfeldertafel ab:
$P (G | M) = \frac{P (M \cap G)}{P (M)} = \frac{\frac{6312}{11101}}{\frac{6399}{11101}} = \frac{6312}{6399} = 0,9864$
Alternativlösung
Da in Teilaufgabe a) schon das Baumdiagramm gezeichnet wurde, lässt sich aus diesem auch ganz einfach $P (G | M)$ ablesen. Du findest den Wert in der zweiten Ebene am obersten Zweig.
$\to P (G | M) = 0,9864$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Placebo eingenommen hat, nicht zu genesen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Zuerst überlegt man sich, welche Wahrscheinlichkeit gesucht ist. Hier sucht man diejenige Wahrscheinlichkeit, mit der eine Person, von der man weiß, dass sie einen Placebo genommen hat, nicht gesund geworden ist.
Das ist $P_{M} G$ .
Verwende die Definition der bedingten Wahrscheinlichkeit und ließ dann die Werte aus der Vierfeldertafel ab.
$P (G | M) = \frac{P (M \cap G)}{P (M)} = \frac{\frac{4390}{11101}}{\frac{4702}{11101}} = \frac{4390}{4702} = 0,9336$
Alternativlösung
In Teilaufgabe a) wurde schon das Baumdiagramm erstellt. Hieraus lässt sich $P_{M} G$ ablesen. Man findet den Wert in der zweiten Ebene, der unterste Zweig.
$\to P_{M} G = 0,9336$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

	$G$	$G$	Summe
$M$	$\begin{array}{l} \frac{6312}{11101} \\ = 0,5686 \end{array}$	$\begin{array}{l} \frac{87}{11101} \\ = 0,0078 \end{array}$	$\begin{array}{l} \frac{6399}{11101} \\ = 0,5764 \end{array}$
$M$	$\begin{array}{l} \frac{312}{11101} \\ = 0,0281 \end{array}$	$\begin{array}{l} \frac{4390}{11101} \\ = 0,3955 \end{array}$	$\begin{array}{l} \frac{4702}{11101} \\ = 0,4236 \end{array}$
Summe	$\begin{array}{l} \frac{6624}{11101} \\ = 0,5967 \end{array}$	$\begin{array}{l} \frac{4477}{11101} \\ = 0,4033 \end{array}$	$1$