Ein Kreisdiagramm (auch Tortendiagramm genannt) ist eine Darstellung von Daten mithilfe von Kreissektoren.
Im Kreisdiagramm stellt der gesamte Kreis den Gesamtwert aller Daten dar. Der Kreis wird in Sektoren eingeteilt.
Die Größe der einzelnen Sektoren entspricht dann dem Anteil am Ganzen.
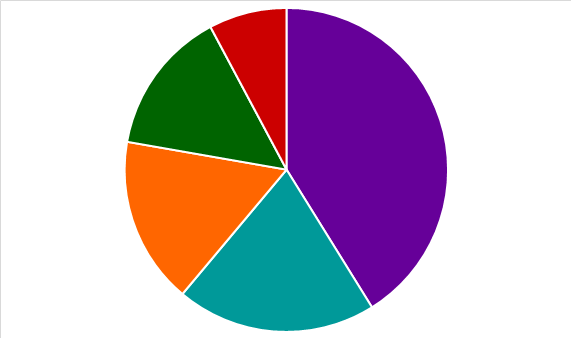
Wie erstellt man ein Kreisdiagramm?
Bestimme die Winkelgrößen der einzelnen Sektoren.
Zeichne einen Kreis mit dem Zirkel.
Zeichne die Sektoren mithilfe der Winkelgrößen in den Kreis.
Füge eine Beschriftung hinzu, damit es übersichtlicher wird.
Anhand dieser Werte kannst du dann die einzelnen Sektoren mit deren Winkelgrößen eintragen.
Winkelgröße bestimmen
Angegeben sind die Daten für das Kreisdiagramm entweder in Prozent oder als absolute Wert.
Berechnung mit Prozentangabe:
Achte darauf, dass die Prozentangaben zusammen ergeben.
Berechnung mit absolutem Wert:
Der Gesamtwert errechnet sich aus der Summer der absoluten Werte.
Einzeichnen der Winkel
Um ein Kreisdiagramm zu zeichnen, brauchst du ein Geodreieck und einen Zirkel.
Kreis zeichnen
Als erstes zeichnest du den Kreis mit deinem Zirkel.

Anfangslinie zeichnen
Danach kannst du dir den Beginn des ersten Abschnittes selbst aussuchen.
Dabei musst du eine Linie beginnend vom Mittelpunkt des Kreises bis zum Rand zeichnen.

Geodreieck anlegen
Als nächstes legst du dein Geodreieck an die Linie an.
Achte dabei darauf, dass die Null des Geodreiecks am Mittelpunkt des Kreises liegt.
In vorherigem Beispiel war der erste Winkel .
Ließ den Winkel ab, in dem du (in diesem Fall) den inneren Gradangaben im Uhrzeigersinn folgst bis du bei angekommen bist.
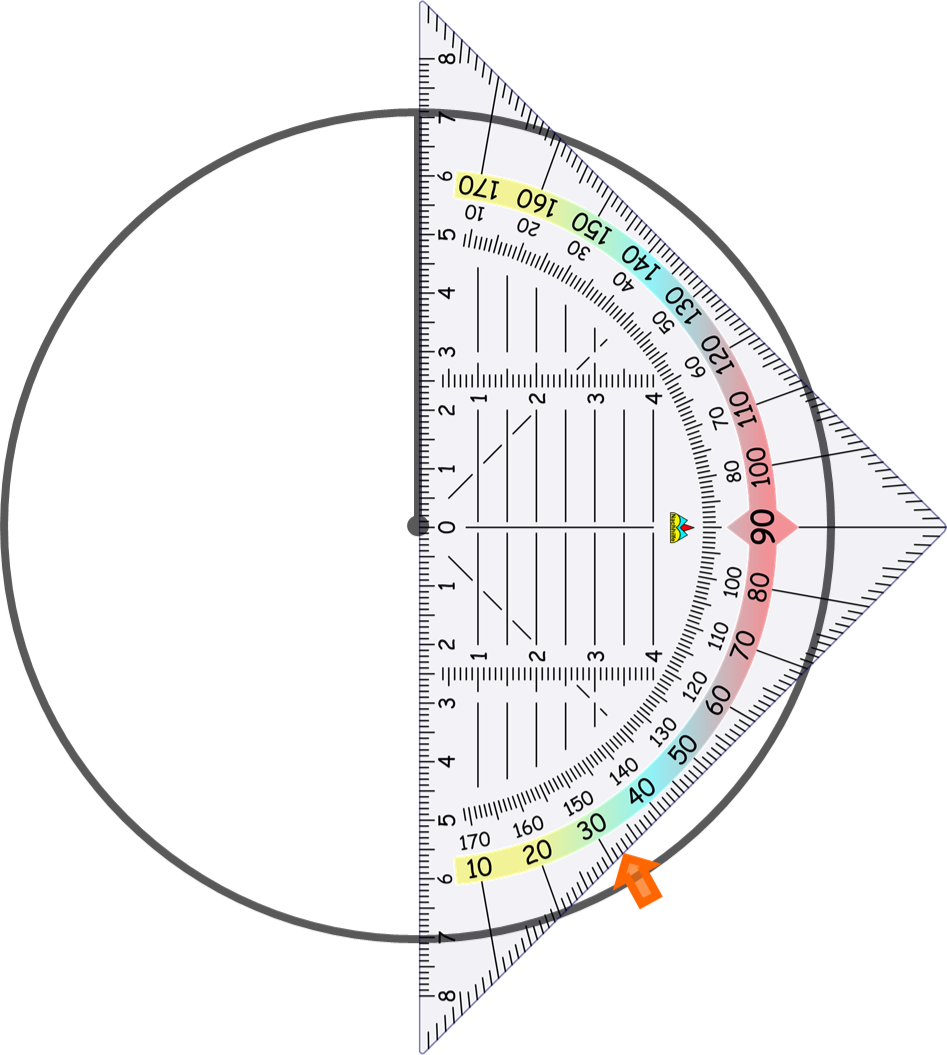
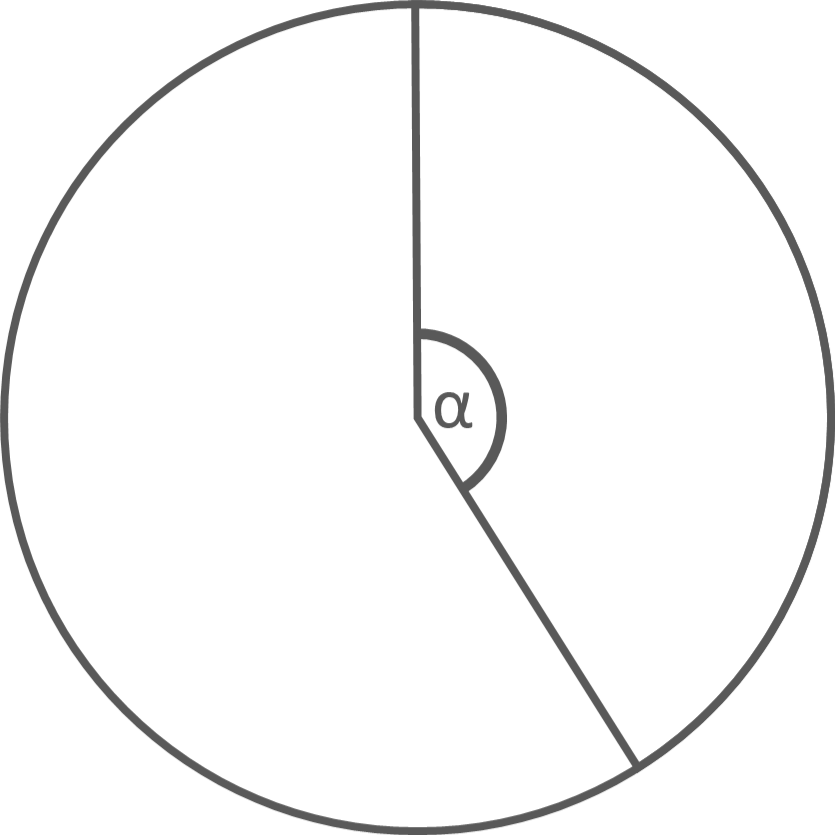
Alpha einzeichen
Markiere dir den Punkt und zeichne eine Linie, die am Mittelpunkt des Kreises beginnt und durch den gerade gekennzeichneten geht, bis zur Kreislinie.
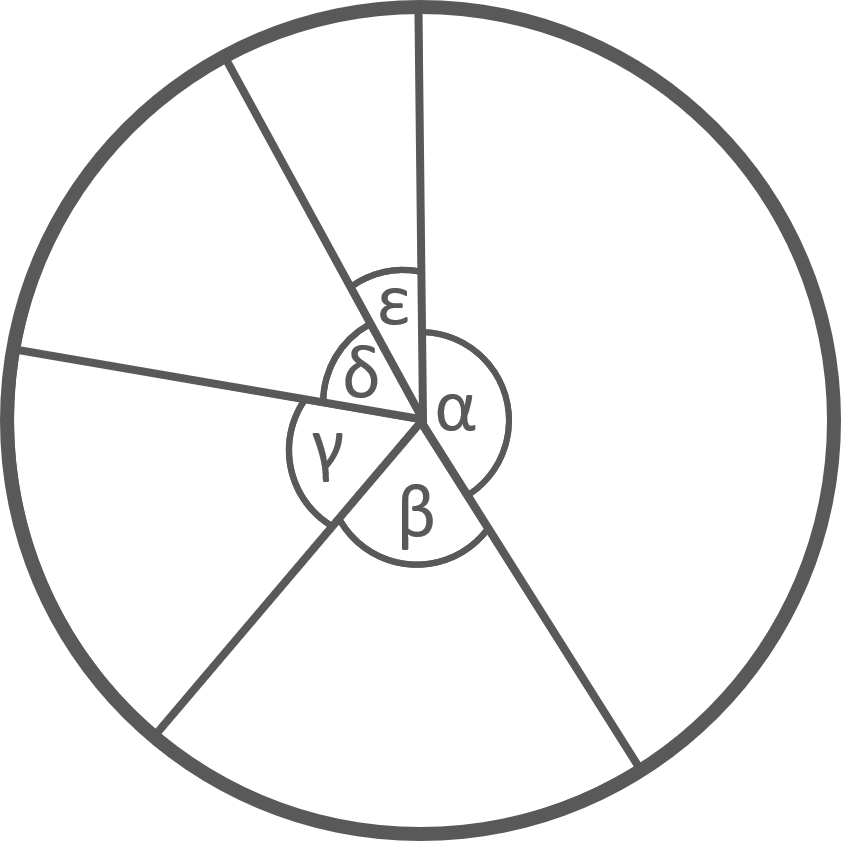
Restliche Linien ergänzen
Das selbe Prinzip gilt auch für die restlichen Abschnitte:
Geodreieck an die neue Linie anlegen und nächsten Winkel abmessen.
Legende hinzufügen
Um das ganze übersichtlicher zu gestalten, kannst du jedem Abschnitt eine eigene Farbe geben.
Zum Schluss fügst du noch eine Beschriftung zu den jeweiligen Kreissegmenten hinzu oder du fügst eine Legende (wie im Bild) hinzu.
Welche Vor und Nachteile hat ein Kreisdiagramm?
Vorteile
Man hat die Aussage schnell im Blick
Nachteile
kann unübersichtlich werden (zum Beispiel bei zu vielen Werten)
Die Genauigkeit der Werte geht verloren
Man kann keine negativen Werte darstellen
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Diagrammen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Wie wertet man ein Diagramm aus?
- Wie erstellt man ein Liniendiagramm?
- Wie erstellt man ein Histogramm?
