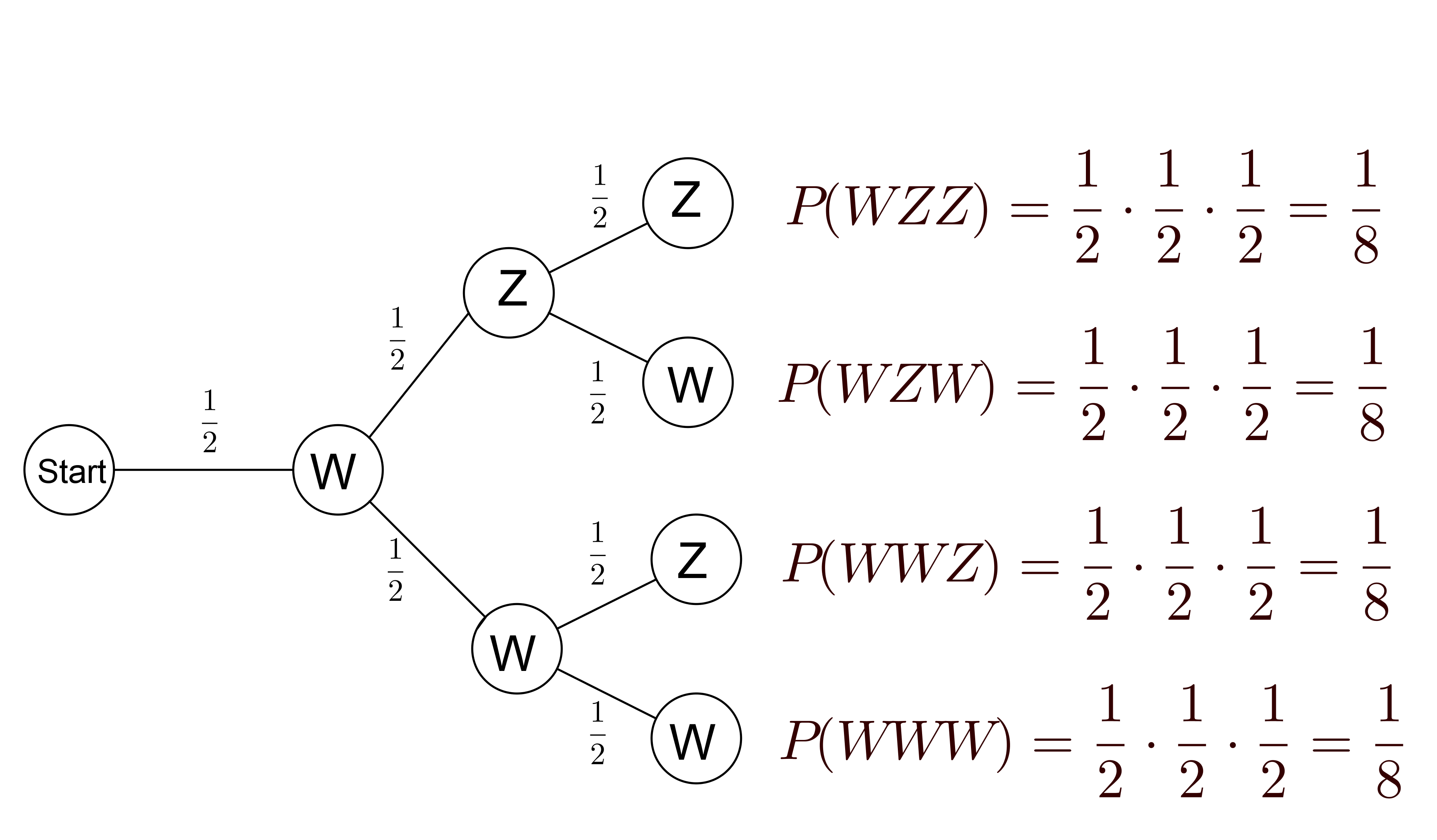Aufgaben zum Baumdiagramm
Hier findest du gemischte Aufgaben zum Baumdiagramm. Lerne das Baumdiagramm zu einem Zufallsexperiment aufzustellen und die Pfadregeln anzuwenden.
- 1
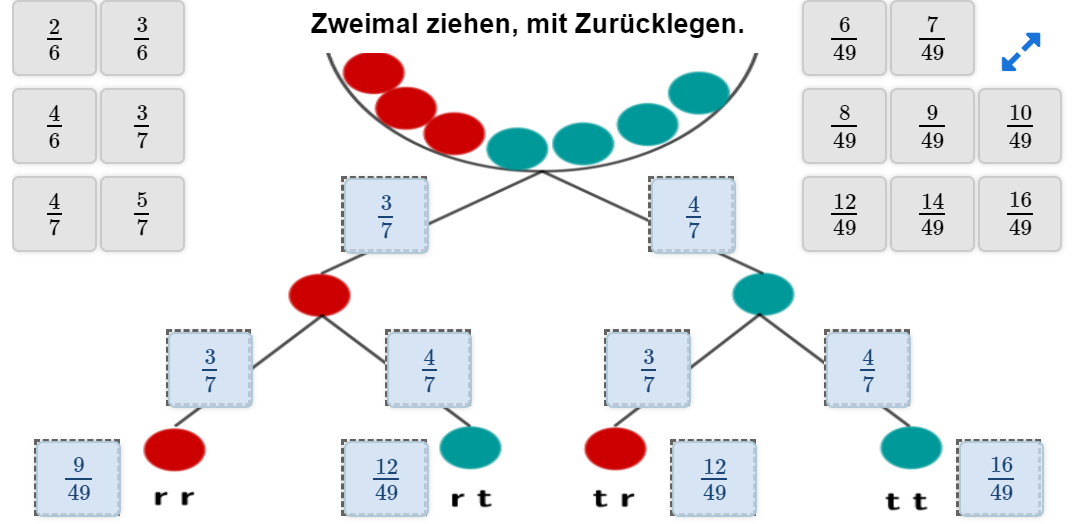
In einer Urne befinden sich drei rote (r) und vier türkisfarbene (t) Kugeln. Es wird zweimal eine Kugel (mit Zurücklegen) gezogen und ihre Farbe notiert.
Ergänze das Baumdiagramm.
- 2
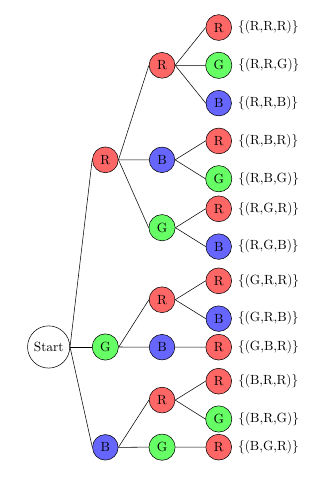
Stefans kleiner Bruder spielt mit seinen Bauklötzen. Er hat drei rote, einen grünen und einen blauen Bauklotz. Wie viele verschiedene Türme aus drei Klötzen kann er bauen? Zeichne ein Baumdiagramm.
- 3
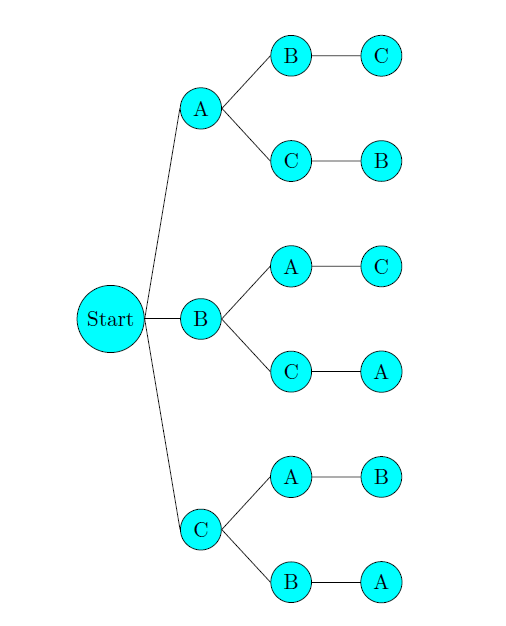
Lucia feiert ihren 11. Geburtstag. Sie hat Angelika (A), Boris (B) und Christoph (C) eingeladen. Sie kommen nacheinander. Bestimme anhand eines Baumdiagramms, wie viele und welche Möglichkeiten ihres Eintreffens es gibt.
- 4
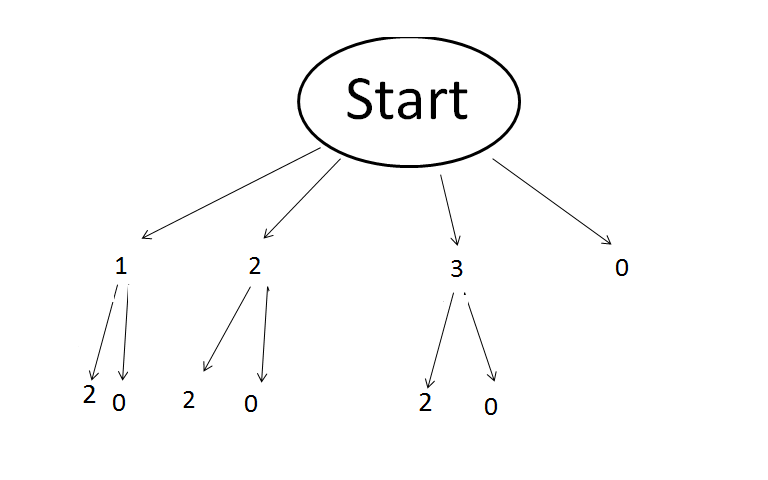
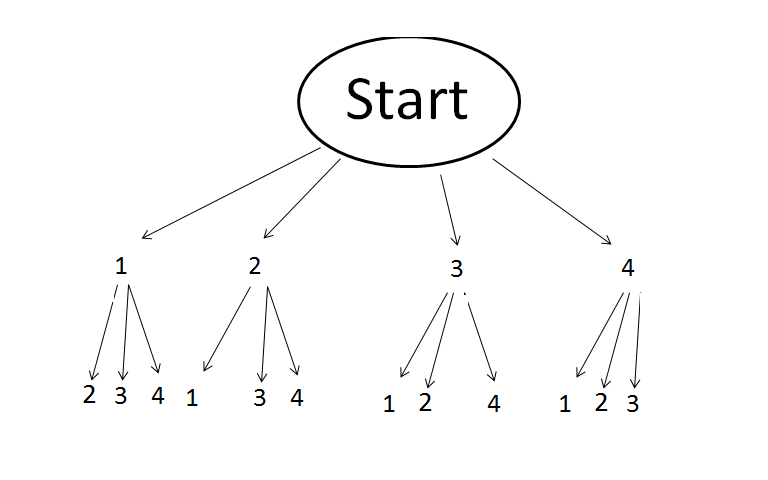
Wie viele gerade zweistellige Zahlen lassen sich aus den Ziffern 0, 1, 2, 3 bilden?
- 5
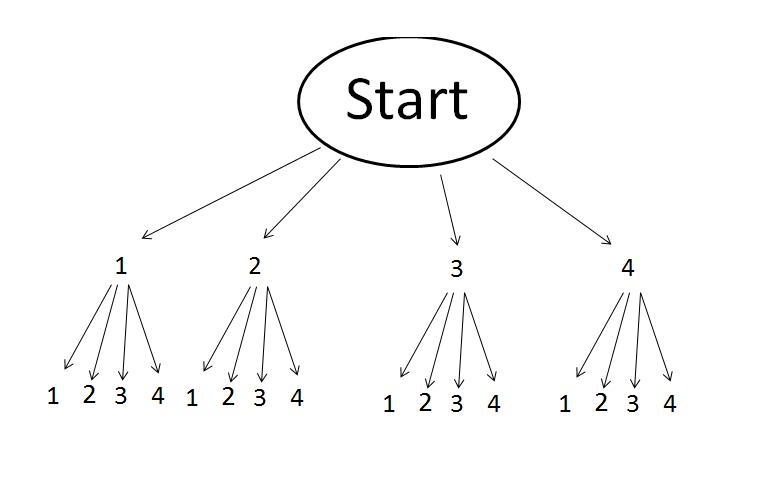
Wie viele zweistellige Zahlen lassen sich aus den Ziffern 1, 2, 3, 4 bilden, wenn keine Ziffer doppelt vorkommen darf?
- 6
Wie viele zweistellige Zahlen lassen sich aus den Ziffern 1, 2, 3, 4 bilden?
- 7
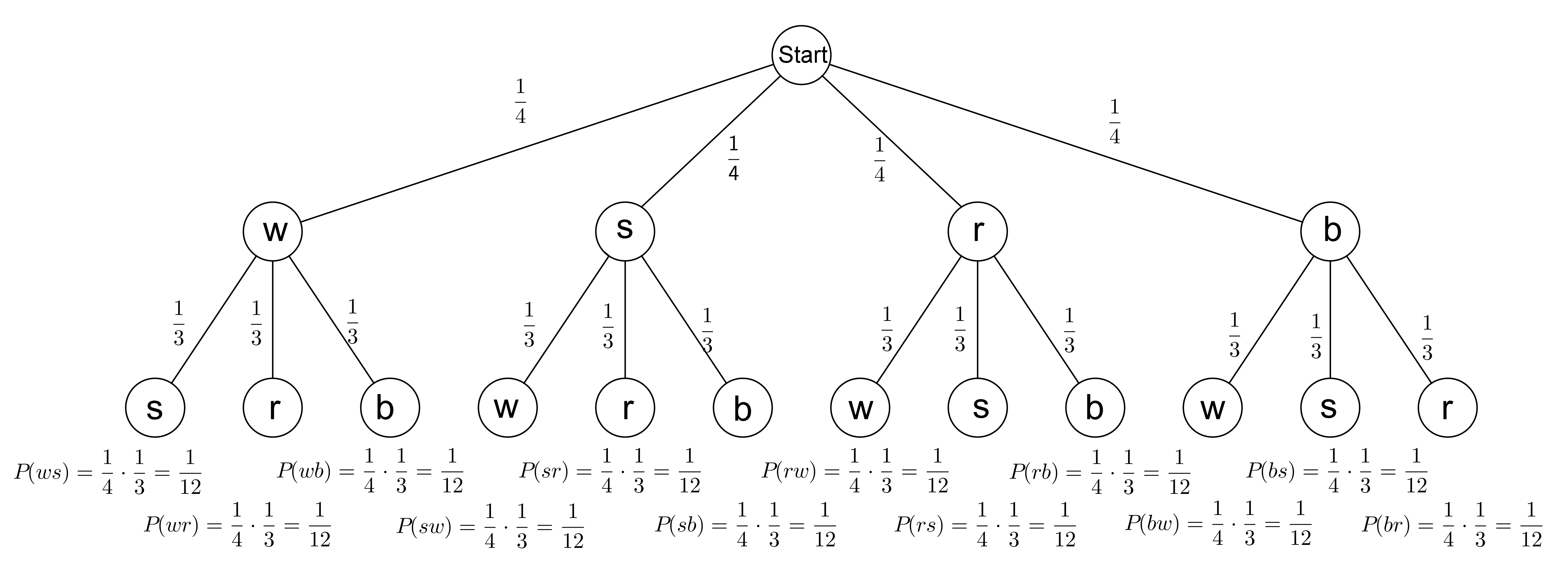
In einer Urne befinden sich eine weiße, eine schwarze, eine rote und eine blaue Kugel. Es werden nacheinander (und ohne Zurücklegen) zwei Kugeln entnommen.
Zeichne ein Baumdiagramm und lies den Ergebnisraum dieses Zufallsexperiments ab.
Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
A: Keine der gezogenen Kugeln ist rot.
B: Unter den gezogenen Kugeln ist eine rote.
C: Es werden zwei rote Kugeln gezogen.
D: Die gezogenen Kugeln sind weiß und schwarz.
Gib in Worten ein Ereignis E mit der Wahrscheinlichkeit und ein Ereignis F mit der Wahrscheinlichkeit an.
- 8
Eine Münze wird dreimal geworfen. Zeichne für folgende Ereignisse die Baumdiagramme und stelle sie in Mengenschreibweise dar.
Hinweis: Die Lösung erfolgt hier mit Hilfe von "Teil-Baumdiagrammen", die nur die für das jeweilige Ereignis günstigen Pfade enthalten. In der nächsten Aufgabe (Aufgabe 8) wird das gesamte Baumdiagramm gezeigt, aus dem sich mit Hilfe der 2. Pfadregel die jeweiligen Wahrscheinlichkeiten ermitteln (also an den Pfaden ablesen und addieren) lassen.
(Z steht für Zahl, W für Wappen)
: "Zahl erscheint höchstens einmal"
: "Wappen erscheint beim ersten Wurf"
: "Es wird nie Wappen geworfen"
- 9
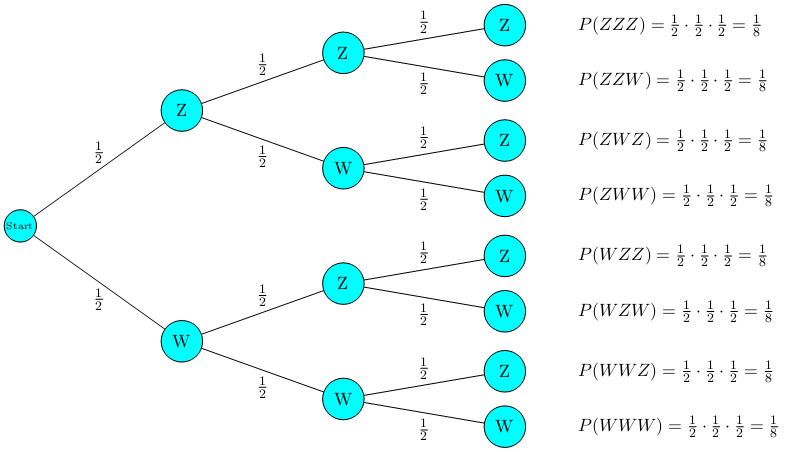
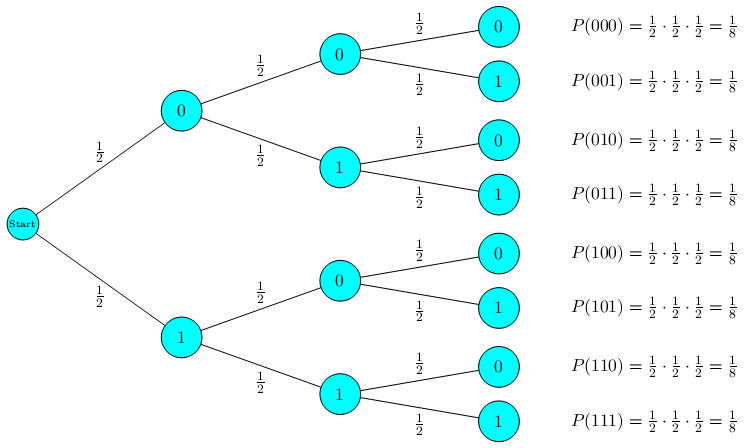
Zeichne den Baum für den dreifachen Münzenwurf Wappen(W) und Zahl(Z) und bestimme die Wahrscheinlichkeiten der einzelnen Ergebnisse.
- 10
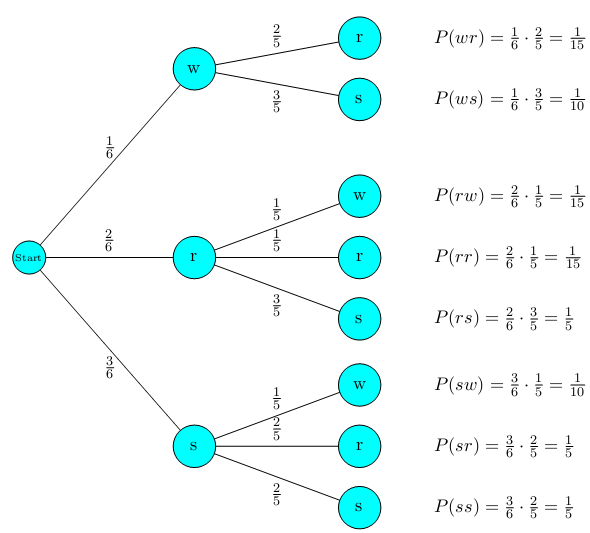
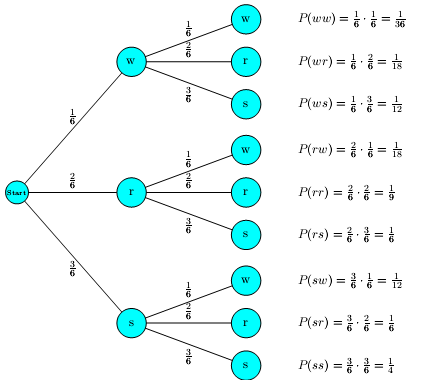
In einer Urne befinden sich 1 weiße, 2 rote und 3 schwarze Kugeln. Man zieht nacheinander zwei Kugeln einmal ohne Zurücklegen und einmal mit Zurücklegen der Kugel nach jedem Zug. Zeichne jeweils ein Baumdiagramm und gib einen Ergebnisraum und seine Mächtigkeit an.
- 11
Max und Tim laden ihren Opa zum Kaffeetrinken ein. Sie haben zwei Stühle und drei Hocker. Ihr Opa muss auf jeden Fall auf einem Stuhl sitzen. Damit es gerecht wird, setzt sich keiner der beiden Jungen auf den Stuhl.
Wie viele Sitzmöglichkeiten gibt es?
- 12
Max und Moritz streiten sich, wer das letzte Eis im Kühlschrank haben darf. Schließlich kommen sie zu dem Entschluss ihre Streitigkeit durch einen Münzwurf beizulegen.
Moritz gewinnt bei Kopf und Max bei Zahl.
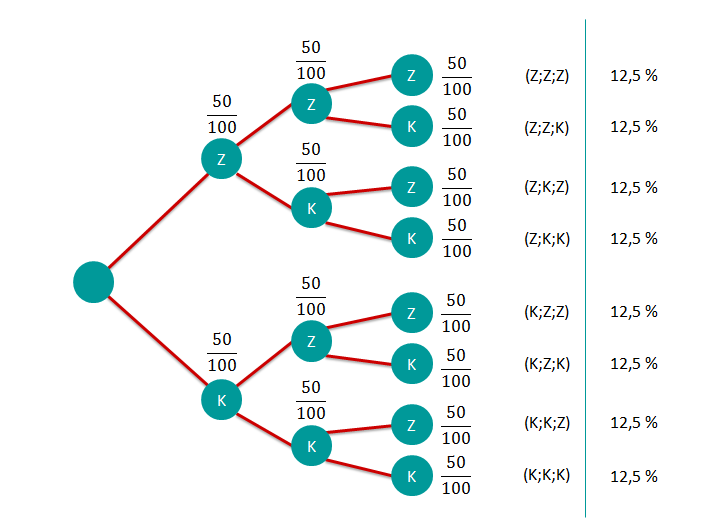
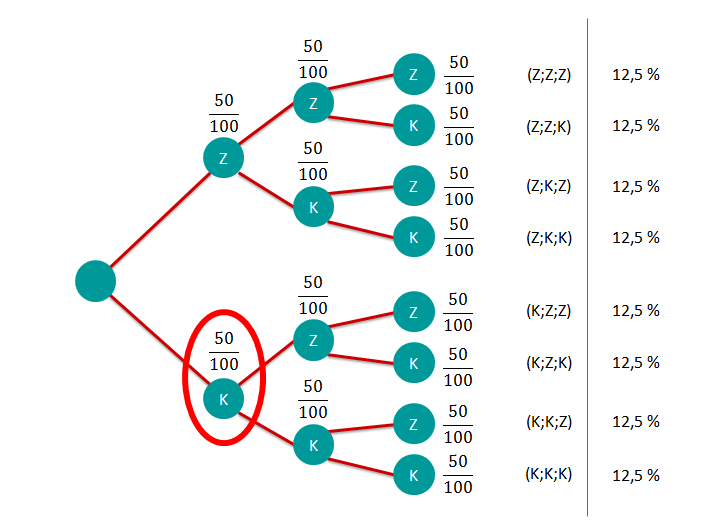
Löse die nachfolgenden Aufgaben mithilfe des nachfolgenden Baumdiagramms.
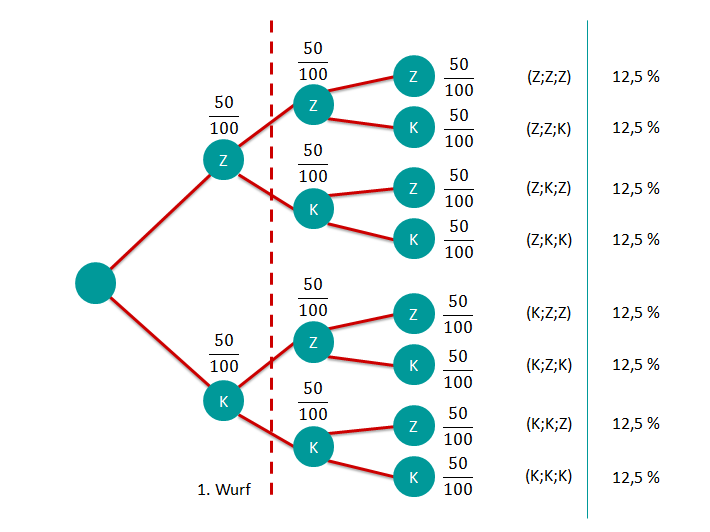
Mit welcher Wahrscheinlichkeit (in Prozent) gewinnt Moritz die erste Runde?
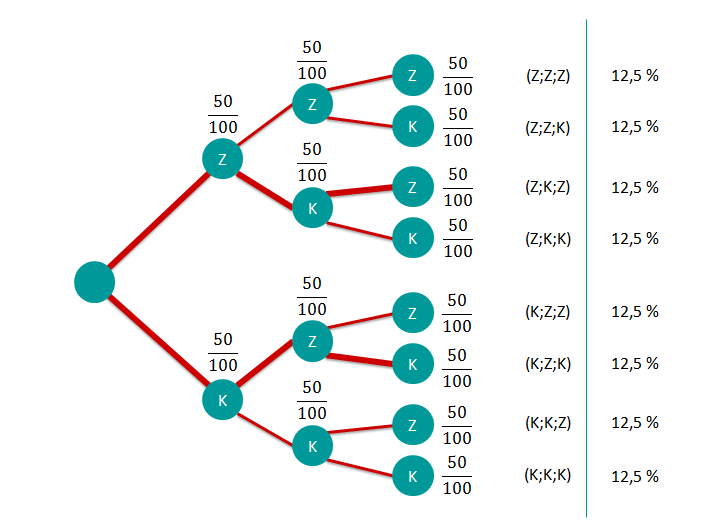
Nachdem Max die erste Runde gewonnen hat, fordert Moritz, dass derjenige gewinnt, der zwei von drei Runden gewinnt. Wie groß ist die Wahrscheinlichkeit, dass Moritz noch gewinnt?
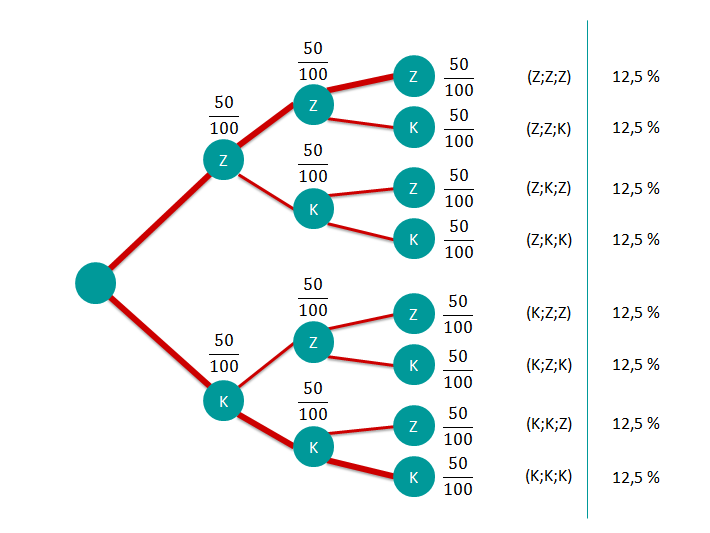
Max behauptet: "Es ist wahrscheinlicher, dass die Münze dreimal auf der selben Seite landet, als abwechselnd (bpsw. Kopf,Zahl,Kopf)
Prüfe ob Max Recht hat, wenn nicht beweise das Gegenteil.
- 13
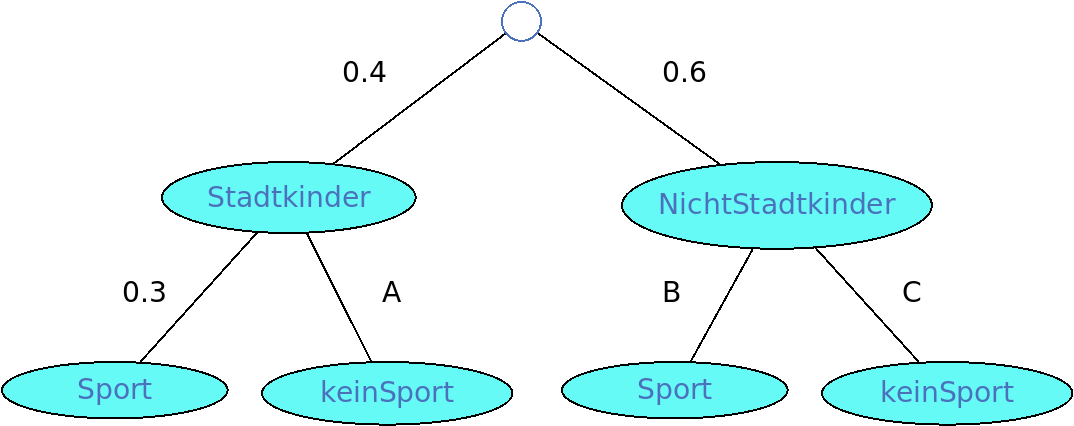
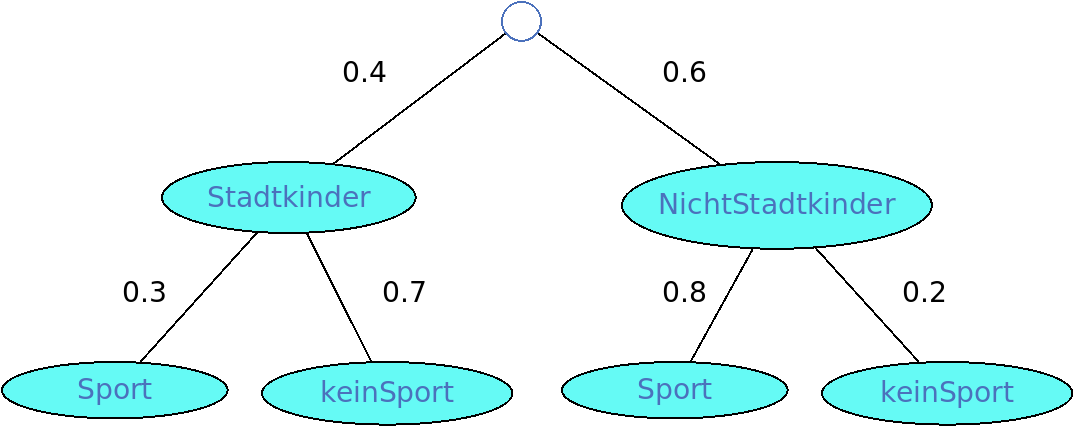
Eine (fiktive) Untersuchung hat gezeigt, dass 40% der Kinder an einer Schule aus der Stadt kommen. Von diesen Stadtkindern treiben 30% regelmäßig Sport.
Insgesamt treiben 60% der Kinder an dieser Schule Sport. Erstelle ein vollständiges Baumdiagramm.
- 14
In einer Urne befinden sich drei rote, zwei blaue und eine grüne Kugel. Es wird zweimal eine Kugel (ohne zurücklegen) gezogen und ihre Farbe notiert.
Urne mit n = 6 Kugeln. Quelle: Wikipedia
Zeichne ein vollständiges Baumdiagramm.
Notiere die folgenden Ereignisse in Mengenschreibweise und berechne ihre Wahrscheinlichkeiten:
: Keine der gezogenen Kugeln ist rot.
: Unter den gezogenen Kugeln ist mindestens eine blaue.
: Es werden zwei gleichfarbige Kugeln gezogen.
: Es werden mehr blaue Kugeln gezogen als rote.
Löse Aufgabe a) und b), wenn die Kugel nach dem ersten Ziehen zurückgelegt wird.
- 15
Eine -Euro-Münze, von der wir annehmen, dass sie eine Laplace-Münze ist, wird mal geworfen.
Liegt die Eins oben, so werten wir den Wurf als , andernfalls als .
Zeichne einen Baum zu diesem Experiment.
Eine Zufallsvariable ordnet jedem Ergebnis aus dem Experiment die Summe der Zahlen zu. Dem Ereignis Zahl-Kopf-Kopf mit dem Wert wird also die Summe zugeordnet. Welche möglichen Summen treten auf? Welche Ergebnisse gehören zu den einzelnen Summen?
- 16
Oma hat in einer Schublade blaue und andersfarbige Kugelschreiber. Bei sieben blauen Kugelschreibern und bei fünf der anderen ist die Mine eingetrocknet.
Erstelle eine vollständig ausgefüllte Vierfeldertafel mit absoluten Häufigkeiten.
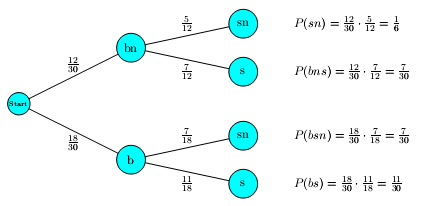
Erstelle ein Baumdiagramm, mit dem die Fragen c) und d) beantwortet werden können.
(b=blau ; bn=nicht blau ; s=schreibt ; sn=schreibt nicht)
Oma greift ohne hinzusehen in die Schublade und nimmt einen Kugelschreiber heraus. Mit welcher Wahrscheinlichkeit ist seine Mine nicht eingetrocknet?
Oma hat einen blauen Kugelschreiber aus der Schublade genommen. Mit welcher Wahrscheinlichkeit „schreibt“ er?
- 17
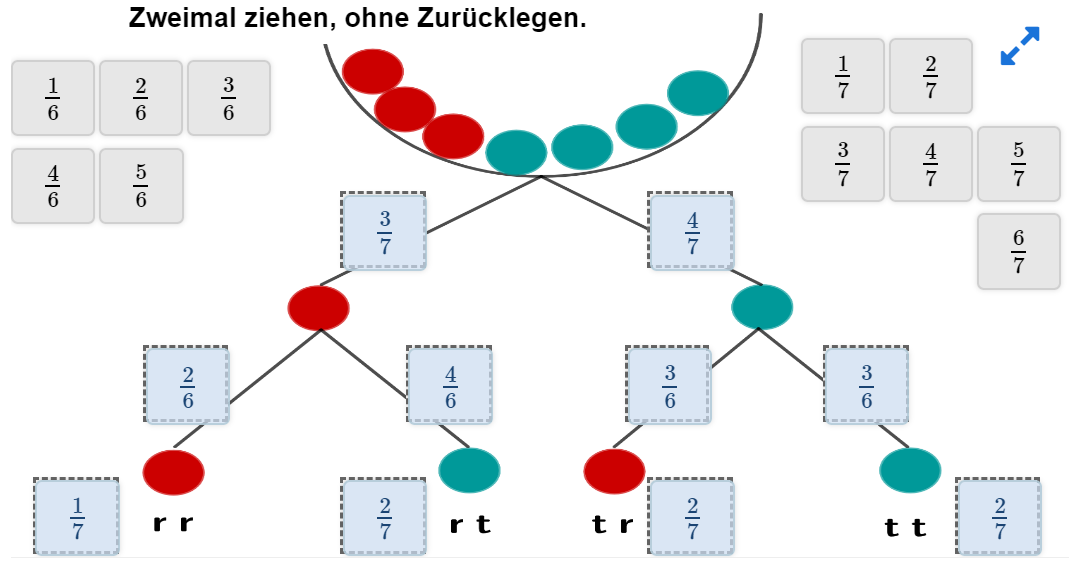
In einer Urne befinden sich drei rote (r) und vier türkisfarbene (t) Kugeln. Es wird zweimal eine Kugel (ohne Zurücklegen) gezogen und ihre Farbe notiert.
Ergänze das Baumdiagramm.
- 18
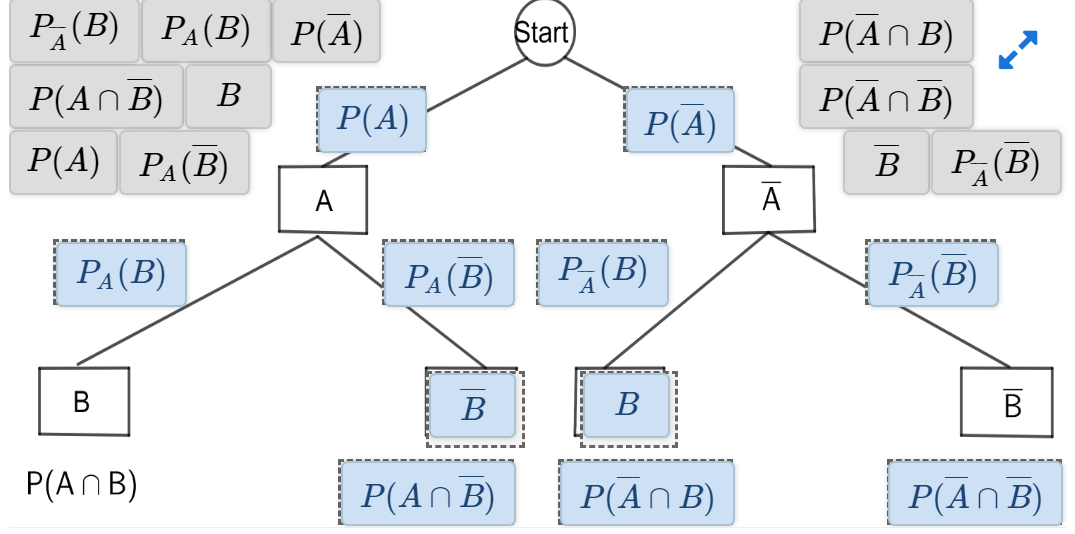
Ordne richtig zu.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?