Die Ergebnismenge oder der Ergebnisraum umfasst alle möglichen Ergebnisse eines Zufallsexperiments.
Bezeichnet wird die Ergebnismenge bzw. der Ergebnisraum meistens mit dem griechischen Buchstaben ("Omega"). (In manchen Lehrbüchern wird auch das Symbol S verwendet.)
Die Ereignismenge ist die Menge aller Ereignisse und nicht dasselbe wie die Ergebnismenge!

Aufstellen eines Ergebnisraumes
Um zu einem Zufallsexperiment einen geeigneten Ergebnisraum zu finden, muss man sich überlegen, welche Ergebnisse bei diesem Experiment theoretisch herauskommen können.
Beispiele
Würfeln mit einem Würfel
Bei einem gewöhnlichen, 6-seitigen Würfel lautet der Ergebnisraum beim Würfeln:
Einmaliges Werfen einer Münze
Beim einmaligen Werfen einer Münze lautet der Ergebnisraum oder auch , wenn man die Ergebnisse entsprechend abkürzen will.
Ziehen von Kugeln aus einer Urne
Die Urne im Bild zeigt unterschiedlich farbige Kugeln. Beim blinden Ziehen gibt es drei Ergebnisse:
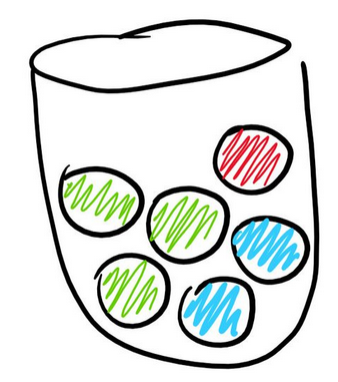
Urne mit den Farben grün, blau, rot
Dreimaliges Werfen einer Münze
Dieser Ergebnisraum lässt sich gut z. B. anhand eines Baumdiagramms ermitteln.
Beim dreimaligen Werfen einer Münze ist ein sinnvoller Ergebnisraum:
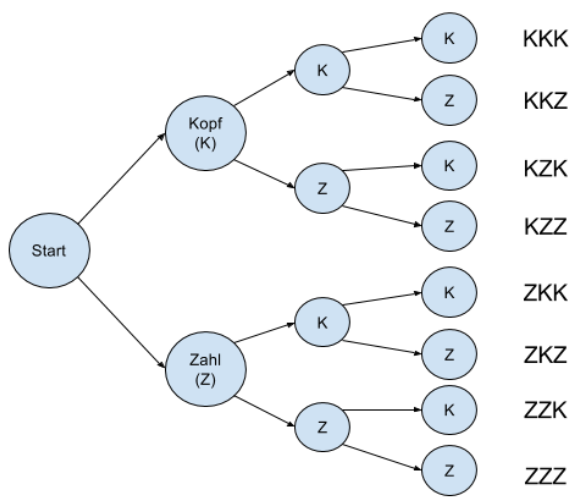
Baumdiagramm zum dreimaligen Werfen einer Münze.
Verschiedene Möglichkeiten für die Wahl des Ergebnisraums bei einem Zufallsexperiment
Einen Ergebnisraum "berechnet" man nicht, sondern man wählt ihn (passend zur Situation der Aufgabe). Trotzdem ist natürlich bei den meisten Aufgaben ein bestimmter Ergebnisraum naheliegend bzw. vernünftig, wie in den obigen Beispielen.
Beispiel
Man zieht aus einem Kartenspiel mit 32 Karten eine beliebige Karte.
Wie können verschiedene Ergebnisräume aussehen?
Welche ist die größte Ergebnismenge?

Lösung:
Man kann sich nur auf die Farbe konzentrieren, dann wäre der Ergebnisraum
Eine weitere Möglichkeit ist, sich die Farbenwerte anzusehen:
oder auch die Kartenwerte:
Schließlich kann man alle Merkmale berücksichtigen:
Die größte Ergebnismenge ist immer die detaillierteste, also mit .
Urnenmodell
Viele Zufallsexperimente können mithilfe eines Urnenmodells simuliert werden.
In der Urne befinden sich Elemente ("Kugeln"), von denen Elemente gezogen werden.
Die Urne kann als Ergebnisraum aufgefasst werden.
Beispiel
Zufallsexperiment:
Ein Würfel wird einmal geworfen und die Augenzahl wird festgestellt.
Zugehöriges Urnenmodell:
In einer Urne befinden sich sechs von 1 bis 6 nummerierte Kugeln, es wird einmal gezogen.
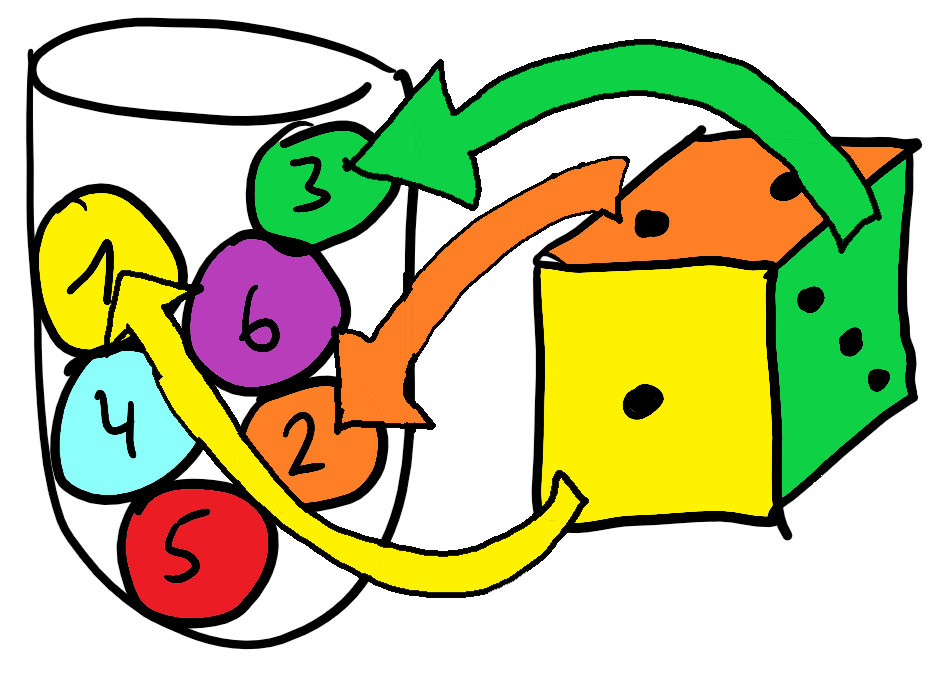
Die Urne links kann das gleiche Zufallsexperiment simulieren, wie der Würfel.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Thema Ergebnisraum oder Ergebnismenge
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
