Aufgaben zu Hypothesentests
Wie gut kennst du dich aus? Mit diesen Aufgaben kannst du dein Wissen zu Hypothesentests vertiefen.
- 1
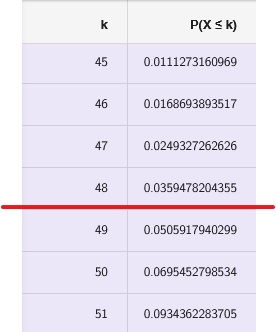
Ein Politiker fällt wiederholt durch negative Äußerungen auf. Während er bei der letzten Wahl in Umfragen noch Zuspruch erhalten hat, geht das Wahlkampfteam mittlerweile davon aus, dass dieser Wert gesunken ist (Gegenhypothese). In einer Stichprobe werden 200 Personen gefragt, wie ihre Meinung zum Politiker ist. 45 Personen geben weiterhin Zuspruch für den Politiker.
Stelle eine Entscheidungsregel auf einem Signifikanzniveau von auf und entscheide anschließend, ob sich die Nullhypothese mit dieser Stichprobe und Entscheidungsregel noch halten lässt.
- 2
Eine Fernsehserie hatte im letzten Jahr eine mittlere Einschaltquote von 10%. Das Management des Senders vermutet, dass die Beliebtheit der Serie im letzten Quartal des Vorjahres sogar etwas zugenommen hat.
Weitere Serien sollen dazugekauft werden, wenn die Beliebtheit der Sendung tatsächlich zugenommen hat. Dazu sollen 200 Personen mittels einer Telefonaktion befragt werden.
Man ist sich auch der Zufälligkeit von Stichprobenergebnissen bewusst und gibt sich mit einer Sicherheit von mindestens 95% des Befragungsergebnisses zufrieden.
Bestimme den Annahme- und Ablehnungsbereich, sowie den tatsächlichen Fehler 1.Art.
- 3
Normalerweise ist jeder zehnte Gallier mit seinem bei Obelix bestellten Hinkelstein unzufrieden, weil er beschädigt ist. Um dies zu überprüfen, befragt Obelix seine letzten 50 belieferten Gallier (und lässt sich natürlich zu einem Wildschwein einladen).
Die Zufallsgröße beschreibt die Anzahl der beschädigten Hinkelsteine.
Wähle den korrekten Ansatz aus und berechne anschließend:
Mit welcher Wahrscheinlichkeit sind mehr als 2, aber weniger als 9 seiner Kunden unzufrieden?
Idefix ist inzwischen sicherer im Apportieren von Hinkelsteinen geworden und lässt nun beim Transport weniger Hinkelsteine fallen. Obelix vermutet deshalb, dass die Anzahl der unzufriedenen Kunden unter 10% gesunken ist. Er befragt erneut 50 Gallier.
Gib die Nullhypothese an, sowie eine Entscheidungsregel für den Fehler 1. Art bei einem Signifikanzniveau von 5%
Entscheide anschließend, ob bei 3 unzufriedenen Galliern Obelix das Prädikat "Mehr als 90% zufriedene Kunden" über seinen Steinbruch schreiben darf.
- 4
In einer Kleinstadt gibt es 2 Grundschulen. Der Schulleiter der Bismarckschule bestreitet, dass im kommenden Schuljahr wieder nur 35% aller Einschulungen an seine Schule kommen. Man habe die Schule schließlich durch viele Zusatzangebote attraktiver gemacht.
Eine Meinungsumfrage mit 200 Eltern soll zeigen, dass die Beliebtheit der Schule gestiegen ist.
Bestimme den Annahme- und Ablehnungsbereich, sowie den tatsächlichen Fehler 1. Art. Skizziere grob die Verteilungsfunktion und kennzeichne die markanten Stellen.
Das Signifikanzniveau sei höchstens 5%.
- 5
Es wird vermutet, dass der Anteil der Befürworter des Rauchverbots an Bushaltestellen und Bahnhöfen in der Bevölkerung gegenwärtig bei höchstens liegt. Um diese Vermutung zu testen, wird eine Befragung von zufällig ausgewählten Personen durchgeführt.
Wie muss die Entscheidungsregel mit einem möglichst großen Ablehnungsbereich lauten, wenn die Vermutung mit einer Wahrscheinlichkeit von höchstens irrtümlich abgelehnt werden soll?
Mit welcher Wahrscheinlichkeit wird bei dieser Entscheidungsregel die Vermutung angenommen, obwohl der Anteil der Rauchverbot-Befürworter tatsächlich beträgt?
- 6
Ein Pharmainstitut behauptet, ein bestimmtes Medikament wirke mit einer Wahrscheinlichkeit von mindestens . Daraufhin wird das Medikament an Personen verabreicht.
In der ersten Testreihe zeigt das Mittel bei der Personen Wirkung. Ist damit die Behauptung des Pharmainstituts auf dem Signifikanzniveau von bewiesen?
Einige Zeit, nachdem das neue Medikament zugelassen ist, bekommt der angesehene Medizinprofessor Dr. Zweifel den Verdacht, das Pharmainstitut habe die Studie gefälscht und das Mittel wirke doch nicht so gut wie behauptet. Er lässt daraufhin erneut einen Test an Personen durchführen. Formuliere für Professor Zweifels Test Nullhypothese und Gegenhypothese. Wie muss seine Entscheidungsregel lauten, wenn er seine Vermutung auf dem Signifikanzniveau von belegen will?
- 7
Nach einer Umfrage eines renommierten Umfrageinstitutes stimmten im Januar der Deutschen für einen schnellen Ausstieg aus der Atomenergie. Aufgrund des steigenden Strompreises mehrten sich Stimmen, die gern bei der Atomenergie bleiben würden, um die Preise niedrig zu halten. Um zu überprüfen, ob sich die öffentliche Meinung geändert hat, wird eine zweite, repräsentative Umfrage mit 200 Personen durchgeführt.
Wie viele Bürger dürfen nun höchstens für einen Ausstieg stimmen, damit die Ergebnisse der ersten Studie auf einem Signifikanzniveau von verworfen werden können?
Angenommen, die aktuelle Zustimmung der Deutschen zur Atomkraft läge bei und der Rest spricht sich für einen schnellen Atomausstieg aus. Mit welcher Wahrscheinlichkeit stimmen dennoch mehr als 160 Leute für einen schnellen Atomausstieg?
- 8
Der Hersteller eines Glücksspielautomaten behauptet, dass die Wahrscheinlichkeit für eine bestimmte Gewinnkombination beträgt. In 200 Spielstunden soll diese Angabe überprüft werden.
Gib die Entscheidungsregel für das Signifikanzniveau an und berechne den Fehler 1. Art. Skizziere grob die Verteilungsfunktion und markiere die markanten Werte.
Bestimme die Wahrscheinlichkeit für den Fehler 2. Art, falls die tatsächliche Wahrscheinlichkeit dieser Gewinnkombination nur beträgt. Skizziere grob die Verteilungsfunktion und markiere die markanten Werte.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?