Die Verteilungsfunktion einer Zufallsgröße ordnet jeder reellen Zahl die Wahrscheinlichkeit zu, mit der höchstens den Wert annimmt.
Man schreibt für die Verteilungsfunktion zur Zufallsgröße :
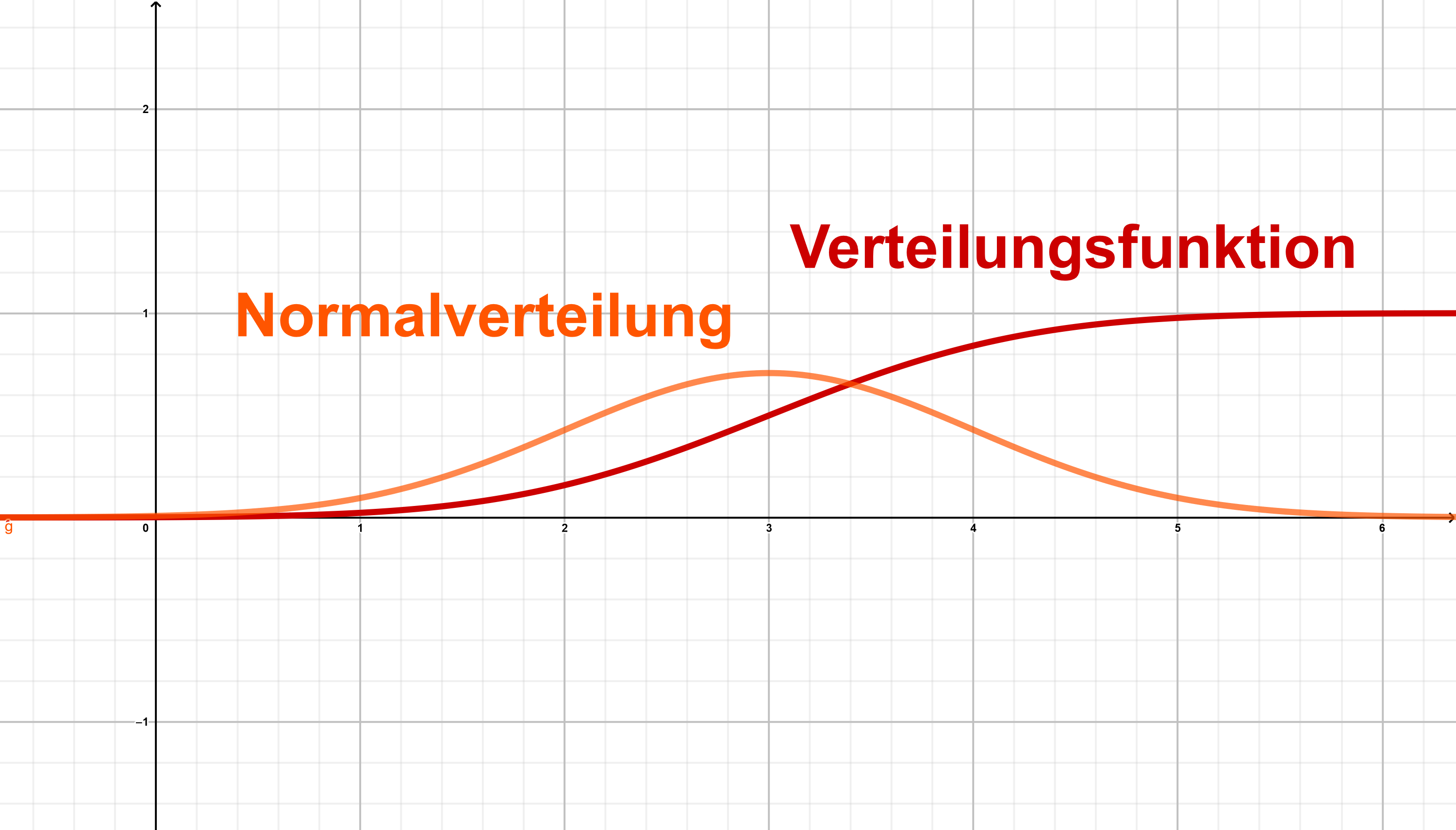
Eigenschaften
ist monoton wachsend
ist rechtsseitig stetig
Rechtsseitig stetig bedeutet, dass der rechtsseitige Grenzwert existiert und gleich dem Funktionswert ist:
Beispiele
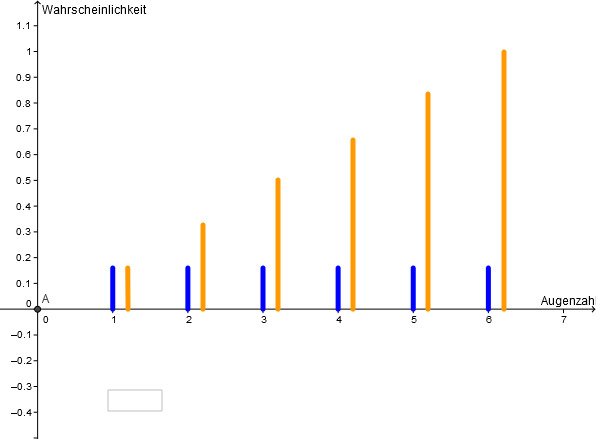
Ein Würfel wird einmal geworfen. Wie wahrscheinlich ist es, dass die Augenzahl kleiner oder gleich 4 ist? Zeichne ein Säulendiagramm für und .
Lösung
Zuerst bestimmen wir die Wahrscheinlichkeiten für die einzelnen Augenzahlen:
1 | 2 | 3 | 4 | 5 | 6 | |
Blau:
Orange:
Ein Spieler einer Fußballmannschaft wird verletzt. Normalerweise dauert die Genesung zwischen und Tagen. Die Zufallsgröße beschreibe die Anzahl der benötigten Tage für die Heilung. Die Wahrscheinlichkeiten sind gegeben durch:
| 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|
| 0 | 0,1 | 0,25 | 0,31 | 0,23 | 0,08 | 0,03 | 0 |
Die Presse möchte wissen, ob der Spieler für das Spiel in Tagen wieder spielfähig ist.
Lösung:
Ein Dartspieler trifft das Bullseye mit einer Wahrscheinlichkeit von . Mit welcher Wahrscheinlichkeit erzielt er bei Würfen mehr als Treffer? Gib außerdem die Verteilungsfunktion an.

Lösung
Berechne die Wahrscheinlichkeiten für die Anzahl der Treffer mit der Binomialverteilung:
0 | 1 | 2 | 3 | 4 | 5 | |
0,07776 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,01024 |
Die Verteilungsfunktion ist gegeben durch:
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Zufallsgrößen und Verteilungsfunktion
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
