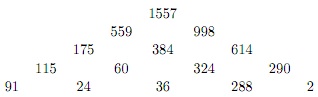Sachaufgaben zu den Grundrechenarten
Lerne das Rechnen mit den Grundrechenarten im Sachkontext mit diesen Übungsaufgaben. Schaffst du sie alle?
- 1
Konrad hat insgesamt 40 € Schulden. Jeden Donnerstag kauft er sich für 2 € eine Pizza. Im Monat bekommt er 15€ Taschengeld. Wie lange braucht er, um seine Schulden zurückzuzahlen?
Monate - 2
Hansi will wissen, wie alt sein Opa ist. Dieser antwortet: Teilt man mein Alter durch 9, dann bleibt der Rest 6. Teilt man 66 durch mein Alter, dann bleibt auch der Rest 6. Berechne zuerst die Lösungsmengen von seiner ersten Antwort, dann die der zweiten Antwort und suche dann das Alter des Großvaters.
- 3
Die kleine Eva stellt der Oma die Frage nach ihrem Alter. „Ach“, sagt die Oma, „wenn man mein Alter durch eine bestimmte Zahl teilt, erhält man Rest . Außerdem habe ich meinen siebzigsten Geburtstag schon hinter mir. Und übrigens, in sechs Jahren bin ich immer noch keine Hundert.“ Wie alt ist die Oma?
Jahre - 4
Wie viele Reiskörner isst ein Mensch in seinem Leben, wenn er 75 Jahre alt wird und täglich ca. g Reis genießt?
Abwiegen von 50 Reiskörnern liefert als Masse ca. 1g.
Reiskörner - 5
Übertrage die Tabelle auf ein Blatt Papier und fülle sie aus.
Vorgänger
Zahl
Nachfolger
?
?
?
?
?
?
?
?
- 6
Setze im Term Klammern so, dass eine Differenz mit möglichst großem Wert entsteht.
- 7
Welche Summe haben die ungeraden Zahlen zwischen 0 und 100? Wie viele gibt es?
- 8
Jutta und Klaus waren bei der Klassensprecherwahl aufgestellt. Jedes Kind in der Klasse hat eine Stimme abgegeben. Die Stimmen wurden aufgeschrieben.
Jutta
Klaus
Jungen
7
5
Mädchen
6
8
Was erfährst du alles?
- 9
Die Aula einer Schule hat 80 Sitzplätze. Für die 5. und 6. Klassen soll ein Film vorgeführt werden. Jede Aufführung kostet 120 Euro.
Klasse
5a
5b
5c
6a
6b
6c
Schüler
32
25
29
30
23
21
Welche Klassen können zusammen eine Aufführung sehen und wie viel muss jeder Schüler an Eintritt zahlen, damit die Schule mit der Aufführung keine Verluste macht?
- 10
In einer Zielscheibe mit konzentrischen Ringen erhält man für den innersten Ring 87 Punkte und für die nach außen darauffolgenden Ringe 73, 59 und 31 Punkte. Bei dieser Zielscheibe wurden mit dem Pfeil genau 301 Punkte erzielt. Finde heraus, wie oft in welche Ringe getroffen wurde.
- 11
Peter geht zum Supermarkt einkaufen. Wie viel muss er bezahlen, wenn er folgende Produkte kauft?
In seinem Geldbeutel hat Peter nur Scheine. Wie viel sollte er von der Kasse zurückbekommen, wenn er mit dem gegebenen Schein zahlt?
Tomatensauce: 3,45 €
Geriebener Käse: 1,85 €
Nudeln: 2,34 €
frisches Basilikum: 1,60 €
Peter zahlt mit einem 50€ Schein.
€Schlagsahne: 0,63€
Butter: 0,80€
Frischkäse: 2,00€
Orangensaft: 1,67€
Shampoo: 3,49€
Peter zahlt mit einem 20€-Schein.
€
- 12
Die Familie Schneider (Mutter, Vater, Tochter, Sohn) ist frisch im Urlaubsort eingetroffen und erkundigt sich an der Liftstation nach den Preisen.
Liftkarten
Erwachsene
Kinder
3-Tages-Karte
74
59
2-Tages-Karte
55
38
Tageskarte
31
23
Nachmittagskarte (gültig ab 12:30 Uhr)
19
13
Hallenbad
2
1,50
Ski- und Snowboardverleih
Dauer
1 Tag
2 Tage
3 Tage
Alpin-Ski (Erwachsene)
20€
31,50
55,50
Alpin-Ski (Kinder)
16,50
26
46
Snowboard
17,50
27,50
48,50
Sonderangebote
Skikurs
25.- pro Person und Tag
Familienangebot
3 Tage für 385 (Lift incl. Ski- oder Snowboard-Ausleihe für alle Familienmitglieder)
Frage
Lohnt sich das Familienangebot?
- 13
Erika möchte ihre Superstarsammlung erweitern. Dazu kauft sie einige Poster, 3CDs, 48 Aufkleber und eine DVD. Insgesamt bezahlt sie 94,13€. Folgende Preise sind bekannt: Ein Aufkleber kostet 39ct, die drei CDs kosten 19,99€ und die DVD 44,50€.
Wie viele Poster kauft sie, wenn eines 91ct kostet?
Poster - 14
In einer ,,Zahlenmauer” erhält man jede Zahl als Summe der Zahlen, die links bzw. rechts darunter liegen. Z. B.
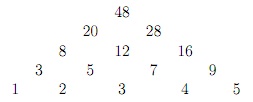
1. Vollende die folgende Zahlenmauer:

2. Kannst du eine Zahlenmauer bauen, bei der…
1. du in der ersten Zeile fünf Zahlen einträgst, die dir gefallen?
2. du in der ersten Zeile nur vier Zahlen vorgibst?
3. in der zweiten Zeile nur ungerade Zahlen vorkommen?
4. in der Spitze eine Zahl nah bei 500 steht?
5. in der Spitze genau 500 steht? Kannst du mehrere Mauern finden, bei denen in der Spitze 500 steht?
6. in der dritten Zeile nur Zahlen vorkommen, die durch drei teilbar sind?
7. du anfangs fünf Zahlen reinschreibst, sodass die Mauer vollendet werden kann?
- 15
Ein Mosaik wird aus weißen und grünen rautenförmigen Fliesen aufgebaut. Die Folge der Figuren beschreibt die ersten 4 Schritte beim Aufbau des Mosaiks. Aus wie vielen Fliesen besteht die 10. Figur, wenn das Muster entsprechend fortgeführt wird?
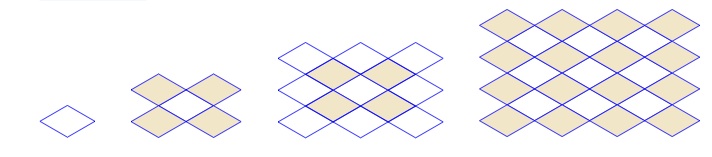 Fliesen enthält die 10. Figur.
Fliesen enthält die 10. Figur. - 16
Tom kauft 8 kleine Bälle und legt sie in eine Tüte, die leer 20 g wiegt. Die Tüte wiegt danach mit den Bällen zusammen 700 g.
Zuhause möchte er gleich mit seiner Schwester spielen und nimmt dazu aus der Tüte 5 Bälle heraus.
Wie viel g wiegt die Tüte jetzt noch?
g - 17
Setze im Term Klammern so, dass
eine Summe entsteht und berechne jeweils die Termwerte.
eine Differenz entsteht und berechne jeweils die Termwerte.
- 18
Während einer Werbeaktion wird jeder Tafel Schokolade der Firma Schoko eine Sammelmarke beigelegt. Für jeweils acht Sammelmarken gibt es im Laden eine Tafel umsonst.
Wie viele Gratistafeln kann man insgesamt für gekaufte Tafeln erhalten?
GratistafelnWie viele Gratistafeln bekommt man, wenn man 2003 Tafeln kauft?
Gratistafeln
- 19
Eine Schule soll in ein anderes Gebäude umziehen. Dazu müssen 1200 Tische transportiert werden. Jeder Tisch hat eine Masse von 24 kg.
Für den Umzug werden Lastwägen eingesetzt, die jeweils mit höchstens 3 t beladen werden dürfen.
Wie viele Lastwägen müssen mindestens fahren, um die Tische zu transportieren?
Wie viele kg können dann auf den letzten Lastwagen noch an anderen Sachen aufgeladen werden?
- 20
In einer ,,Zahlenmauer” erhält man jede Zahl als Summe der Zahlen, die links bzw. rechts darunter liegen. Z. B.
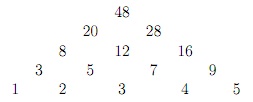
Vollende die folgende Zahlenmauer:
Kannst du eine Zahlenmauer bauen, bei der…
1. du in der ersten Zeile fünf Zahlen einträgst, die dir gefallen?
2. du in der ersten Zeile nur vier Zahlen vorgibst?
3. in der zweiten Zeile nur ungerade Zahlen vorkommen?
4. in der Spitze eine Zahl nah bei steht?
5. in der Spitze genau steht? Kannst du mehrere Mauern bauen, bei denen in der Spitze steht?
6. in der dritten Zeile nur Zahlen vorkommen, die durch drei teilbar sind?
7. du anfangs fünf Zahlen reinschreibst, sodass die Mauer vollendet werden kann?
- 21
Einkaufen
Daniel soll für seine Eltern einkaufen gehen. Dazu bekommt er 10€ mit.
Er soll an der Käsetheke 250g Käse(100g kosten 1,10€) und beim Metzger 200g Schinken(100g kosten doppelt so viel wie 100g Käse) kaufen.
Wie viel bezahlt er insgesamt?
 €
€Jetzt ist Daniel im Supermarkt. Er soll 8 Äpfel für jeweils 40ct kaufen. Es gibt Äpfel aber auch in 4er Packungen für je 1,50€.
Er möchte besonders günstig einkaufen.
Wie viel bezahlt er am Ende?

Daniel geht jetzt zum Getränkemarkt, um einen Kasten Wasser mit 6 Flaschen zurückzubringen. Für jede Flasche erhält er 8ct. Für den Kasten bekommt er zusätzlich 12ct.
Wie viel Geld bekommt er insgesamt heraus?
ctEr ist fertig mit dem Einkauf für seine Eltern und möchte sich nun von dem restlichen Geld Gummibärchen(eins je 6ct) kaufen.
Wie viel Geld hat er bis jetzt ausgegeben und bekommen?
Wie viele Gummibärchen kann er sich leisten?

- 22
Familie Schwarz hat für neue Kinderzimmermöbel gespart
Sie hat folgende Möbelstücke auf der Wunschliste:
1 Bett für
1 Schrank für
1 Spieltisch für
1 Schreibtisch für
1 Sofa für
Was kosten die Möbelstücke insgesamt? Reicht das angesparte Geld?
Sind bestimmte Gegenstände nicht notwendig? Markiere diejenigen, die nicht notwendig sind.
- 23
Bauunternehmer Eder verkauft kleine Gartenhäuschen, die er seinen Kunden selbst im Garten aufbaut und mit roten Dachziegeln deckt.
In diesem Jahr hat er schon mehrere solcher Häuschen verkaufen können:

Als erstes verkaufte er ein Häuschen an seinen Nachbarn Tobias. Das Häuschen gefiel Thomas, der Zwillingsbruder von Tobias, so gut, dass er gleich darauf auch eines für seinen Garten bestellt.
Ein paar Wochen später kaufte Herrn Eders Cousine Anneliese ein Gartenhäuschen, und kurz darauf Rocco aus dem Nachbarort.
Zuletzt wollte auch noch Annette, die Nachbarin von Rocco, ein Gartenhäuschen von Herrn Eder haben.
Für alle diese Häuschen zusammen hat Herr Eder 1750 Dachziegel gebraucht.
Wie viele dieser Dachziegel liegen (insgesamt) auf den Dächern von den Gartenhäuschen der Zwillinge Tobias und Thomas?
DachziegelHerr Eder musste die Dachziegel in Packungen zu je 500 Stück kaufen. Bei den Arbeiten sind allerdings 19 Ziegel zerbrochen. Wie viele Ziegel hat er später noch übrig?
- 24
Bei einem Fahrradwettbewerb gehen zwei Profifahrer namens Herr Schnell und Herr Sportlich an den Start. Beide benötigen normalerweise für eine lange Strecke .
Heute fahren sie eine lange Strecke. Herr Schnell fällt jedoch zu Beginn zurück und ist nach erst weit. Nun beschleunigt er und fährt den Rest der Strecke mit pro .
Wie lange braucht Herr Schnell?
minWie lange braucht Herr Sportlich?
minWer ist als Erster im Ziel?
- 25
Übertrage die Tabelle in dein Heft und gib von jeder Zahl den Vorgänger und Nachfolger an.
Vorgänger
Zahl
Nachfolger
999
9099
266
4089
19999
520900
- 26
Karla geht oft ins Freibad. Sie bezahlt dafür 3 EUR Eintritt. Eine Zehnerkarte kostet 25 EUR.
Wie viel Geld könnte sich Karla sparen wenn sie die Zehnerkarte benutzen würde?
€Ab wie vielen Besuchen würde sich die Zehnerkarte lohnen?
Besuchen
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?