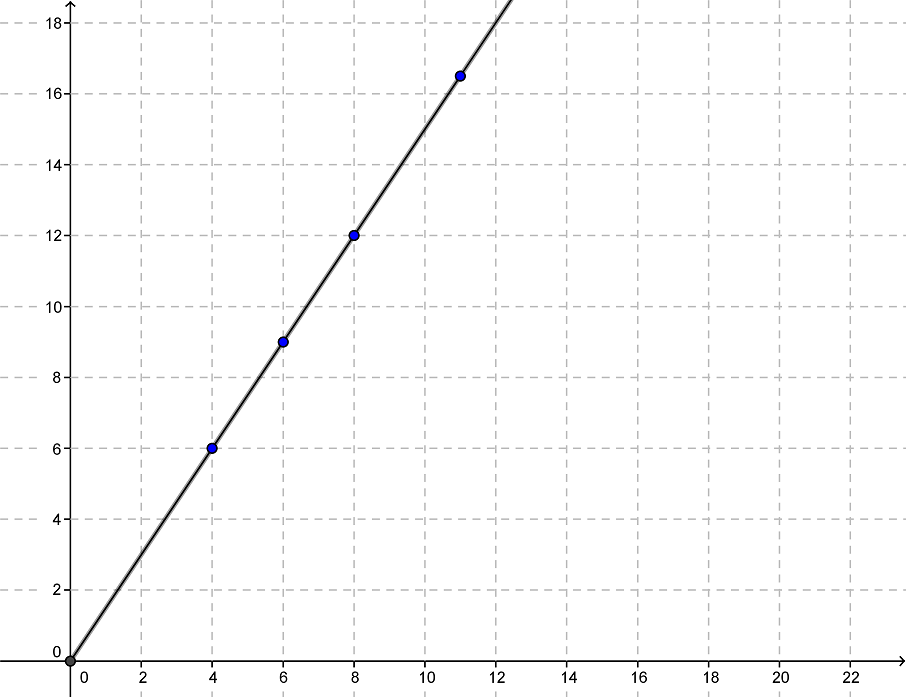
Die folgende Wertetabelle enthält direktproportionale Wertepaare. Berechne die fehlenden Werte und trage die Wertepaare in ein Gitternetz ein.
Menge in Liter | 4 | 6 | 8 | ||
|---|---|---|---|---|---|
Preis in € | 6 | 12 | 16,5 |
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?