Der Grundwert ist ein wichtiger Bestandteil in der Prozentrechnung. In diesem Artikel lernst du anhand von Beispielen und kleinschrittigen Erklärungen die verschiedenen Arten des Grundwertes, wie du diese erkennst und mit Hilfe der Formeln oder des Dreisatzes berechnest.
Der Grundwert
Der Grundwert ist die ganze Menge oder die gesamte Anzahl. Er entspricht 100 Prozent.
Die Formel dafür lautet
Wobei den Prozentwert und den Prozentsatz beschreibt.
Hinweis: In anderen Bundesländern sind auch die Bezeichnungen für Grundwert, für Prozentwert und für Prozentsatz gebräuchlich.
Beispiel zum Grundwert:
Bei der Klassensprecherwahl erhält Johannes 7 Stimmen. Das heißt, 25 % der Klasse haben ihn gewählt. Wie viele Schüler sind insgesamt in Johannes’ Klasse?
Gegeben:
Prozentwert: Prozentsatz:
Gesucht:
Grundwert
1. Variante: Dreisatz

Antwort: In Johannes’ Klasse sind insgesamt 28 Schüler.
2. Variante: Formel
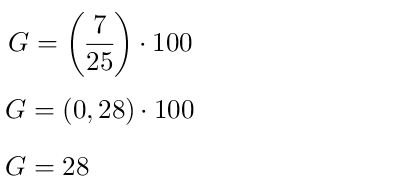
Antwort: In Johannes’ Klasse sind insgesamt 28 Schüler.
Tipp: Falls du dich noch einmal absichern möchtest, kannst du mit deinem Ergebnis noch einmal zurückrechnen. (Wenn 25 % von deinem Ergebnis 7 sind, kannst du dir sicher sein, dass dein Ergebnis richtig war.)
Der verminderte Grundwert
Der Grundwert kann jedoch auch verringert werden, dann spricht man von einem verminderten Grundwert. Wie der Name schon sagt, geht es hier um die Reduzierung des Grundwertes. Rabatte sind ein gutes Beispiel. Diese werden vom Grundwert, den 100 %, abgezogen. Das Ergebnis wird dann verminderter Grundwert genannt, da er nun weniger als 100 % beträgt.
Die Formel für den verminderten Grundwert lautet
wobei der Prozentsatz ist, um den der Grundwert vermindert wird.
Beispiel zum verminderten Grundwert:
Laura möchte sich eine Handtasche für 150 € kaufen. In einem Onlineshop ist diese um 20 % reduziert. Wie viel kostet die Handtasche in dem Onlineshop?

Gegeben:
Grundwert:
Prozentsatz:
Gesucht:
verminderter Grundwert
Hinweis: Der Grundwert beträgt jetzt 80 % des ursprünglichen Grundwertes.
1. Variante: Dreisatz
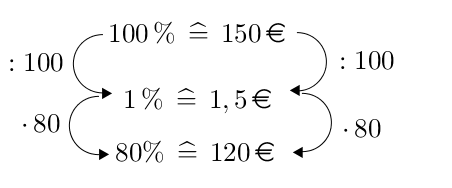
Antwort: Die Handtasche in dem Onlineshop kostet 120 €.
2 Variante: Formel
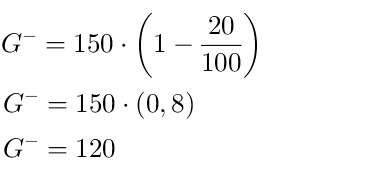
Antwort: Die Handtasche in dem Onlineshop kostet 120 €.
Tipp: Wie oben kannst du wieder eine Umkehrrechnung machen. (Mit hast du die Aufgabe richtig gelöst.)
Der vermehrte Grundwert
Wenn der Grundwert erhöht wird, spricht man von einem vermehrten Grundwert. Dazu kommt es zum Beispiel bei Preiserhöhungen oder Steueraufschlägen. Diese werden dann zu dem Grundwert addiert, sodass man einen vermehrten Grundwert erhält.
Die Formel für den vermehrten Grundwert lautet
wobei der Prozentsatz ist, um den der Grundwert vermehrt wird.
Beispiel zum vermehrten Grundwert:
Der Preis für ein Handy hat sich um 10 % erhöht. Vor der Preiserhöhung hat das Handy 260 € gekostet. Wie viel kostet das Handy jetzt?

Gegeben:
Grundwert:
Prozentsatz:
Gesucht:
vermehrter Grundwert
Hinweis: Der Grundwert ist jetzt 10 % höher als der ursprüngliche Grundwert.
1. Variante: Dreisatz
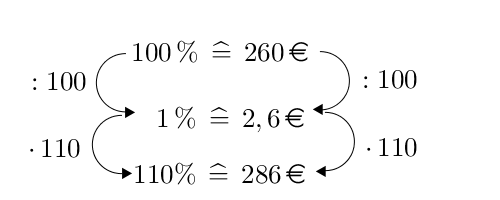
Antwort: Das Handy kostet jetzt 286 €.
2. Variante: Formel:
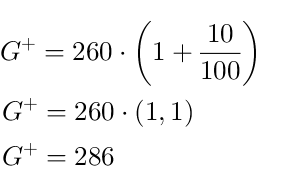
Antwort: Das Handy kostet jetzt 286 €.
Jetzt weißt du, was der Begriff Grundwert in der Prozentrechnung bedeutet, und bist dazu bereit selbständig Aufgaben zum verminderten und vermehrten Grundwert zu lösen.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu vermehrtem und vermindertem Grundwert
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
