Eine Dreisatzberechnung kann bei vielen Umformungen helfen. Auch bei der Prozentrechnung kommt man mit einem Dreisatz und zwei Rechenschritten ans Ziel.
Alle drei möglichen Aufgabentypen (Prozentwert, Grundwert und Prozentsatz suchen) sind durch Dreisätze lösbar! Alternativ zum Prozentrechnen mit Dreisatz kann man auch direkt über Formeln den gesuchten Wert bestimmen. Siehe dazu auch den Artikel Prozentrechnung mit Formeln.
Für eine grundsätzliche Erklärung und Anschauung zum Prozentzeichen und seiner Bedeutung kannst du den Artikel Prozent durchlesen.
Der Dreisatz
Der Dreisatz stellt ein Verfahren dar, um eine direkte Proportionalität zwischen zwei Größen zu berechnen. Er ist daher ideal, um Aufgaben zur Prozentrechnung zu lösen! Mehr zum Thema Dreisatz findest du im Artikel Dreisatz.
Beispielaufgaben zur Prozentrechnung
Folgende Beispiele sollen dir erklären, wie man den Prozentwert, Grundwert und Prozentsatz findet.
Hinweis: Der Artikel Prozentrechnung mittels Formeln löst die gleichen Aufgaben auf eine andere Art und Weise.
Prozentwert gesucht
Beispiel
Wie viel Euro sind von € ?
Lösung:

Antwort: von € sind €.
Grundwert gesucht
Beispiel
Eine Ware wurde um verbilligt und kostet jetzt €. Was kostete sie vorher?
Lösung:
Die Ware wurde um billiger, kostet also nur noch des Ausgangspreises (siehe Bild rechts).
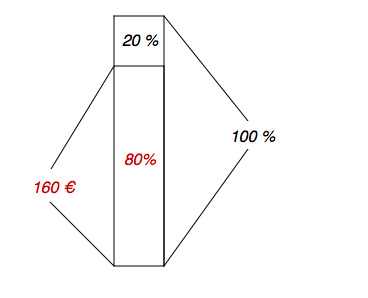
Die Berechnung mit dem Dreisatz erfolgt dann so:
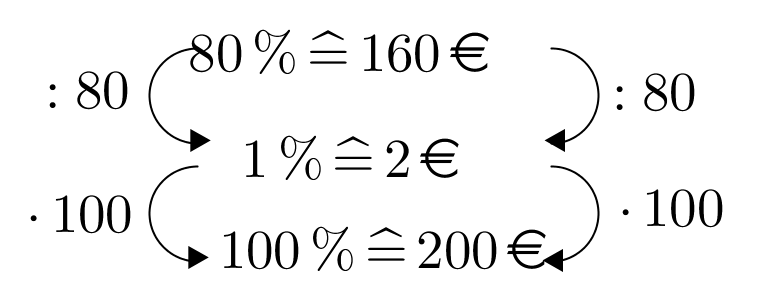
Antwort: Die Ware kostete vorher €.
Prozentsatz gesucht
Beispiel
Von den Schülern haben zu Hause eine Katze. Wie viel Prozent der Klasse sind das?
Lösung:

Antwort: Es sind der Klasse.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Prozentrechnung
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
