Mithilfe des Dreisatzes werden Werte in drei Schritten umgerechnet, wobei immer als Bezug der Wert verwendet wird.
Sind zwei Größen, wie "Anzahl von Stunden" und "Gelaufene Kilometer" zueinander proportional, können unbekannte Werte mit einem Dreisatz bestimmt werden.
Es gibt auch den umgekehrt proportionalen / antiproportionalen Fall, bei denen mit dem sogenannten umgekehrten Dreisatz gerechnet wird.
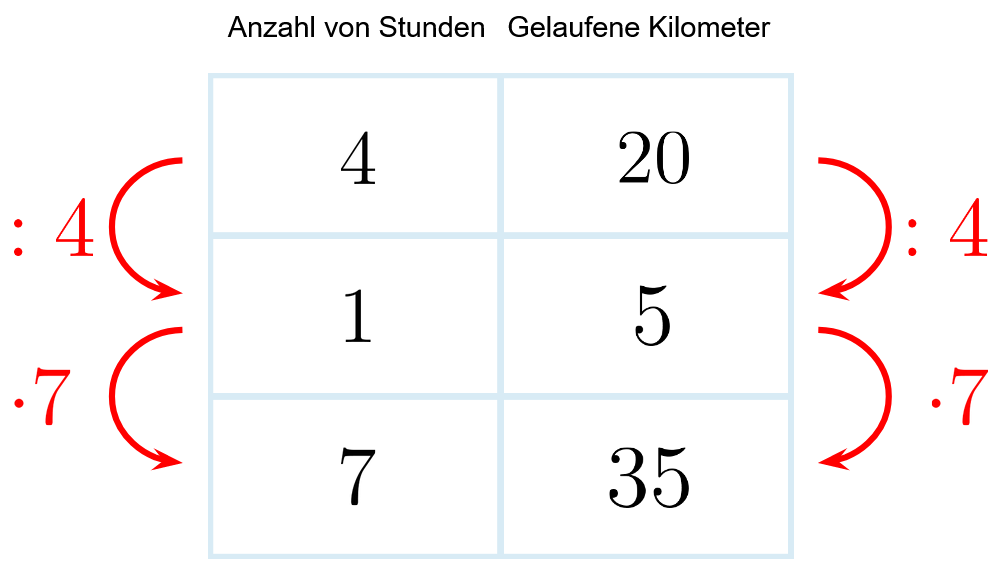
Erklärung am Beispiel
Hast du schon einmal Pfannkuchen gemacht? Das Rezept ist sehr einfach, für Personen benötigst du außer Eiern und Salz, g Mehl und ml Milch. Angenommen, du würdest Personen zum Essen einladen, dann wäre es die doppelte Menge an Zutaten. Doch wie viele Zutaten brauchst du, wenn Personen eingeladen sind?
Umrechnung der Milch
Aus dem Rezept wissen wir, dass Personen ml benötigen. Da es nicht einfach ist direkt von auf Personen mit einem Faktor zu schließen, verwenden wir einen Trick:
Wir berechnen die Menge Milch, die eine Person benötigt, mit einer Division. Von da aus können beliebige Werte mit einer simplen Multiplikation bestimmt werden.
Es ergibt sich also:
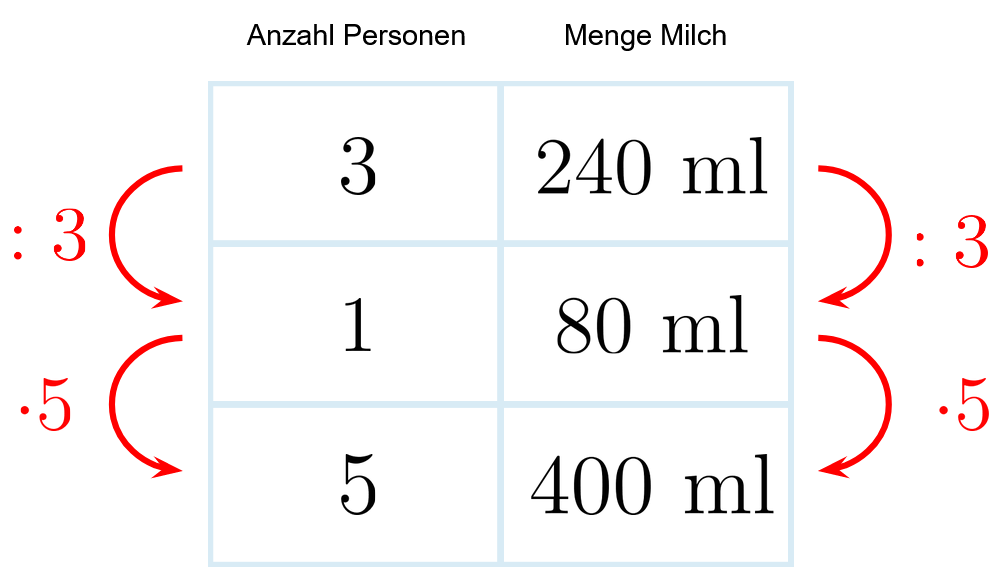
Umrechnung des Mehls
Dieselbe Rechnung wird für das Mehl durchgeführt.
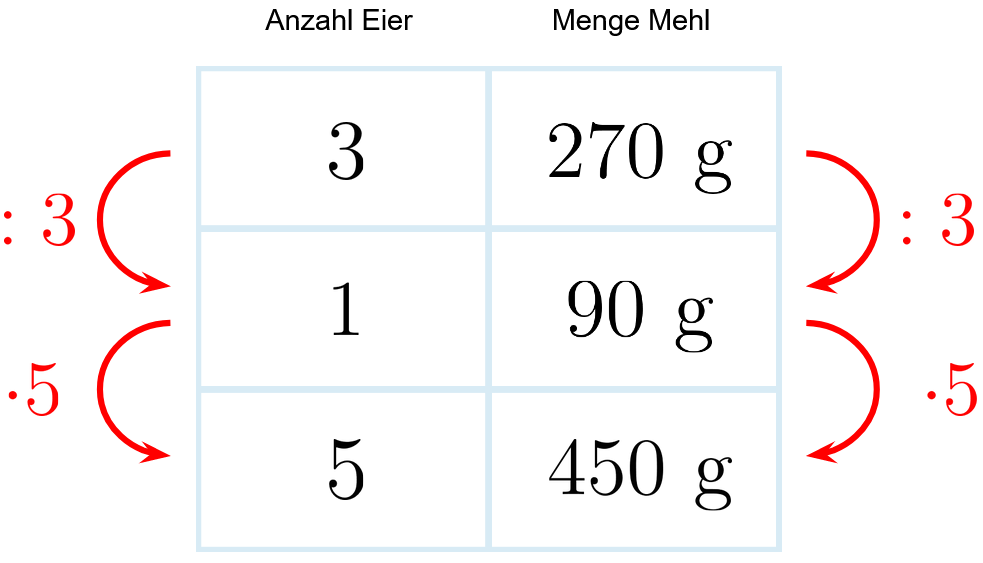
Insgesamt lässt sich das Rezept für Personen zu ml Milch und g Mehl berechnen.
Da auf beiden Seiten der Gleichung
unterschiedliche Größen stehen, mit verschiedenen Einheiten, kann kein in der Mitte stehen. Anstatt dessen sagt man: " Personen entsprechen der Menge von g Mehl."
Allgemeines Vorgehen
Einige Schritte sind beim Dreisatz immer gleich, sodass das Verfahren auf alle Umrechnungen allgemein formuliert werden kann.

Mit dem richtigen Faktor kann eine Umrechnung zwischen zwei Werten direkt erfolgen und muss nicht über den Zwischenschritt mit der getan werden.
Mithilfe des Bruchs kann direkt von auf gerechnet werden:

Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Dreisatz
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
