Geometrie der Ebene: Flächen
- 1
Rechteck, Quadrat, Trapez oder Parallelogramm? Wähle aus.
Beachte: Mehrere Antworten können richtig sein.

Das Bild zeigt ein Rechteck. Jedes Rechteck ist auch ein besonderes Parallelogramm. Und jedes Parallelogramm ist auch ein besonderes Trapez. Daher stimmen die Antworten: Rechteck, Trapez und Parallelogramm.
Hast du eine Frage oder Feedback?

Das Bild zeigt ein Quadrat. Jedes Quadrat ist ein besonderes Rechteck. Jedes Rechteck ist auch ein besonderes Parallelogramm. Und jedes Parallelogramm ist auch ein besonderes Trapez. Daher stimmen alle Antworten: Rechteck, Quadrat, Trapez und Parallelogramm.
Hast du eine Frage oder Feedback?
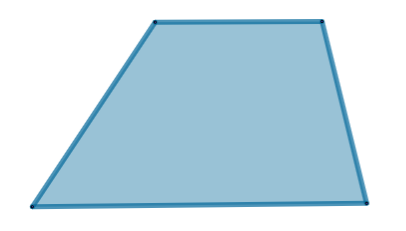
Das Bild zeigt ein Parallelogramm. Jedes Parallelogramm ist auch ein besonderes Trapez. Daher stimmen die Antworten: Trapez und Parallelogramm.
Hast du eine Frage oder Feedback?

Das Bild zeigt ein Quadrat. Jedes Quadrat ist ein besonderes Rechteck. Jedes Rechteck ist auch ein besonderes Parallelogramm. Und jedes Parallelogramm ist auch ein besonderes Trapez. Daher stimmen alle Antworten: Rechteck, Quadrat, Trapez und Parallelogramm.
Hast du eine Frage oder Feedback?

Das Bild zeigt ein Parallelogramm. Jedes Parallelogramm ist auch ein besonderes Trapez. Daher stimmen die Antworten: Trapez und Parallelogramm.
Hast du eine Frage oder Feedback?

Das Bild zeigt ein Rechteck. Jedes Rechteck ist auch ein besonderes Parallelogramm. Und jedes Parallelogramm ist auch ein besonderes Trapez. Daher stimmen die Antworten: Rechteck, Trapez und Parallelogramm.
Hast du eine Frage oder Feedback?
- 2
Ist der Winkel > 90°, < 90° oder = 90°? Wähle die richtige Antwort aus.
- 3
Was ist auf dem Bild eingezeichnet? Der Radius oder der Durchmesser? Wähle die richtige Antwort aus.
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Radius.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Radius.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Durchmesser.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Radius.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Durchmesser.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Radius.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Durchmesser.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Radius.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser .
Im Bild sieht man also den Durchmesser.
Hast du eine Frage oder Feedback?
- 4
Schreibe für jeden Kreis auf, wie lang der Radius oder der Durchmesser ist.
Wie lang ist der Durchmesser?
Nimm die 30 mal 2 und schon hast du den Durchmesser.
Rechnung:
Der Durchmesser beträgt 60.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser
Wie lang ist der Durchmesser?
Nimm die 6 mal 2 und schon hast du den Durchmesser.
Rechnug:
Der Durchmesser beträgt 12.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser
Wie lang ist der Radius?
Teile die 12 durch 2 und schon hast du den Radius.
Rechnung:
Der Radius beträgt 6.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser
Wie lang ist der Durchmesser?
Nimm die 2 mal 2 und schon hast du den Durchmesser.
Rechnung:
Der Durchmesser beträgt 4.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser
Wie lang ist der Radius?
Teile die 24 durch 2 und schon hast du den Radius.
Rechnung:
Der Radius beträgt 12.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser
Wie lang ist der Radius?
Teile die 8 durch 2 und schon hast du den Radius.
Rechnung:
Der Durchmesser beträgt 8.
Hast du eine Frage oder Feedback?
Als Radius bezeichnet man die Strecke vom Mittelpunkt bis zur Kreislinie.
Der doppelte Radius ist der Durchmesser
- 5
Richtige oder falsche Eigenschaften? Kreuze die richtigen Antworten an.
Ein Quadrat ist ein besonderes Rechteck. Das Quadrat hat dieselben Eigenschaften wie das Rechteck und zudem sind alle 4 Seiten gleich lang.
Alle 4 Winkel des Quadrats sind rechte Winkel. Die Summe der vier rechten Winkel heißt Winkelsumme und beträgt 360 °.
Hast du eine Frage oder Feedback?
Bei einem Rechteck sind die gegenüberliegenden Seiten gleich lang und parallel zueinander. Das Rechteck hat 4 rechte Winkel.
Hast du eine Frage oder Feedback?
Bei einem Parallelogramm sind die gegenüberliegenden Seiten parallel zueinander. Die gegenüberliegenden Winkel sind gleich groß.
Hast du eine Frage oder Feedback?
Ein Viereck mit genau einem Paar paralleler Seiten nennt man Trapez und wie jedes andere Viereck besitzt es vier Ecken.
Hast du eine Frage oder Feedback?
- 6
Berechne den Flächeninhalt und Umfang.
Im Bild sieht man ein Rechteck mit den Seitenlängen und
Umfang
Das Rechteck hat einen Umfang von .
Flächeninhalt
Das Rechteck hat einen Flächeninhalt von .
Hast du eine Frage oder Feedback?
Im Bild siehst du ein Quadrat mit der Seitenlänge .
Umfang
Das Quadrat einen Umfang von .
Flächeninhalt
Das Quadrat hat einen Flächeninhalt von .
Hast du eine Frage oder Feedback?
Im Bild siehst du ein Quadrat mit Seitenlänge .
Umfang
Das Quadrat hat einen Umfang von .
Flächeninhalt
Das Quadrat hat einen Flächeninhalt von .
Hast du eine Frage oder Feedback?
Im Bild siehst du ein Rechteck mit den Seitenlängen und .
Umfang
Das Rechteck hat einen Umfang von .
Flächeninhalt
Das Rechteck hat einen Flächeninhalt von .
Hast du eine Frage oder Feedback?
- 7
Überlege: Wie lang sind die fehlenden Seitenlängen der Rechtecke?
Das Rechteck hat einen Flächeninhalt von . Die Seite hat die Länge . Überlege dir, mit welcher Zahl du mal nehmen musst, um zu erhalten.
Du erhältst die fehlende Zahl, indem du durch teilst.
Die fehlende Seite hat die Länge .
Probe:
(Die Seiten und sind gleich lang. Daher ist das Rechteck sogar ein Quadrat.)
Hast du eine Frage oder Feedback?
Das Rechteck hat einen Flächeninhalt von . Die Seite hat die Länge . Überlege dir, mit welcher Zahl du mal nehmen musst, um zu erhalten.
Du erhältst die fehlende Zahl, indem du durch teilst.
Die fehlende Seite hat die Länge .
Probe:
Hast du eine Frage oder Feedback?
Das Rechteck hat einen Flächeninhalt von . Die Seite hat die Länge . Überlege dir, mit welcher Zahl du mal nehmen musst, um zu erhalten.
Du erhältst die fehlende Zahl, indem du durch teilst.
Die fehlende Seite hat die Länge .
Probe:
(Die Seiten und sind gleich lang. Daher ist das Rechteck sogar ein Quadrat.)
Hast du eine Frage oder Feedback?
Das Rechteck hat einen Flächeninhalt von . Die Seite hat die Länge . Überlege dir, mit welcher Zahl du mal nehmen musst, um zu erhalten.
Du erhältst die fehlende Zahl, indem du durch teilst.
Die fehlende Seite hat die Länge .
Probe:
(Die Seiten und sind gleich lang. Daher ist das Rechteck sogar ein Quadrat.)
Hast du eine Frage oder Feedback?
Das Rechteck hat einen Flächeninhalt von . Die Seite hat die Länge . Überlege dir, mit welcher Zahl du mal nehmen musst, um zu erhalten.
Du erhältst die fehlende Zahl, indem du durch teilst.
Die fehlende Seite hat die Länge .
Probe:
Hast du eine Frage oder Feedback?
Das Rechteck hat einen Flächeninhalt von . Die Seite hat die Länge . Überlege dir, mit welcher Zahl du mal nehmen musst, um zu erhalten.
Du erhältst die fehlende Zahl, indem du durch teilst.
Die fehlende Seite hat die Länge .
Probe:
Hast du eine Frage oder Feedback?
- 8
Überlege: Wie groß ist der Umfang der Dreiecke?
- cm
Den Umfang des Dreiecks erhältst du, indem du die Seitenlänge addierst.
Das Dreieck hat den Umfang .
Hast du eine Frage oder Feedback?
- cm
Den Umfang des Dreiecks erhältst du, indem du die Seitenlänge addierst.
Das Dreieck hat den Umfang .
Hast du eine Frage oder Feedback?
- cm
Den Umfang des Dreiecks erhältst du, indem du die Seitenlänge addierst.
Das Dreieck hat den Umfang .
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?