1 Lösung 1b
Aufgabenstellung
Betrachtet wird der abgebildete Würfel . Die Eckpunkte , , und dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: , , und .
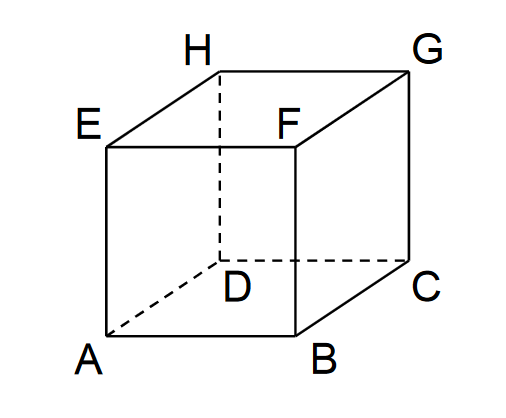
a) Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen Sie diese. Geben Sie die Koordinaten des Punkts an. (2 BE)
b) Der Punkt liegt auf der Kante des Würfels und hat vom Punkt den Abstand . Berechnen Sie die Koordinaten des Punkts . (3 BE)
Lösung
Das erste, was dir auffallen sollte ist, dass der Abstand:
Die zweite Information, die dich ab diesem Schritt weiterbringt, ist, dass auf der Kante liegt. Deshalt haben und die gleiche - und -Koordinate.
Mit dieser Erkenntnis kannst du auch die verbliebene dritte Koordinate des Punktes finden.
Rechne die mögliche(n) Lösung(en) für aus.
Da sowohl , als auch auf der selben -Koordinatenachse liegen, muss der Wert von zwischen und liegen.
Die dritte Koordinate für ist entweder oder . Da allerdings nicht in der Menge liegt, bleibt dir nur noch eine Möglichkeit.
Die Koordinaten des Punktes sind also .
2 Aufgabe 2
Gegeben sind die Punkte und .
a) Bestimmen Sie die Koordinaten des Punkts so, dass gilt: . (2 BE)
b) Durch die Punkte und verläuft die Gerade . Betrachtet werden Geraden, für welche die Bedingungen und gelten:
Jede dieser Geraden schneidet die Gerade orthogonal.
Der Abstand jeder dieser Geraden vom Punkt beträgt .
Ermitteln Sie eine Gleichung für eine dieser Geraden. (3 BE)
3 Lösung 2a
4 Lösung 2b
Aufgabenstellung
Gegeben sind die Punkte und .
a) Bestimmen Sie die Koordinaten des Punkts so, dass gilt: . (2 BE)
Betrachtet werden Geraden, für welche die Bedingungen und gelten:
Der Abstand jeder dieser Geraden vom Punkt beträgt .
Lösung
Die allgemeine Geradengleichung in der analystischen Geometrie lässt sich schreiben als
Bestimmung der Geradengleichung
Die angegebene Gerade soll durch die Punkte und verlaufen. Deswegen wählt man als Stützvektor den Ortsvektor und als Richtungsvektor .
Bestimmung der neuen Geradengleichung
Sei die allgemeine Geradengleichung der neuen Gerade
Bedingung : Orthogonalität
Zwei Vektoren stehen orthogonal zueinander, wenn sie senkrecht aufeinander stehen. Dies ist der Fall, falls ihr Skalarprodukt Null ergibt. Bei Geraden überprüfst du diese Bedingung, indem du das Skalarprodukt ihrer Richtungsvektoren bildest.
Allerdings bekommst du eine Gleichung mit drei Unbekannten. In solch einem Fall darfst du zwei Unbekannte frei auswählen. Du kannst hierfür z. B. und für wählen. Dann gilt
Der Richtungsvektor der neuen Gerade lautet also
Bedingung : Abstand
Es fehlt nur noch der Stützpunkt der Gerade . Dieser soll zum Stützpunkt der Gerade den Abstand haben.
Wie du auch auf dem Bild rechts erkennen kannst, gibt es zwei Möglichkeiten, eine passende Gerade zu finden. Der Stützpunkt bzw. haben den Abstand zu dem Punkt . Deswegen musst du in zwei Schritten denken:
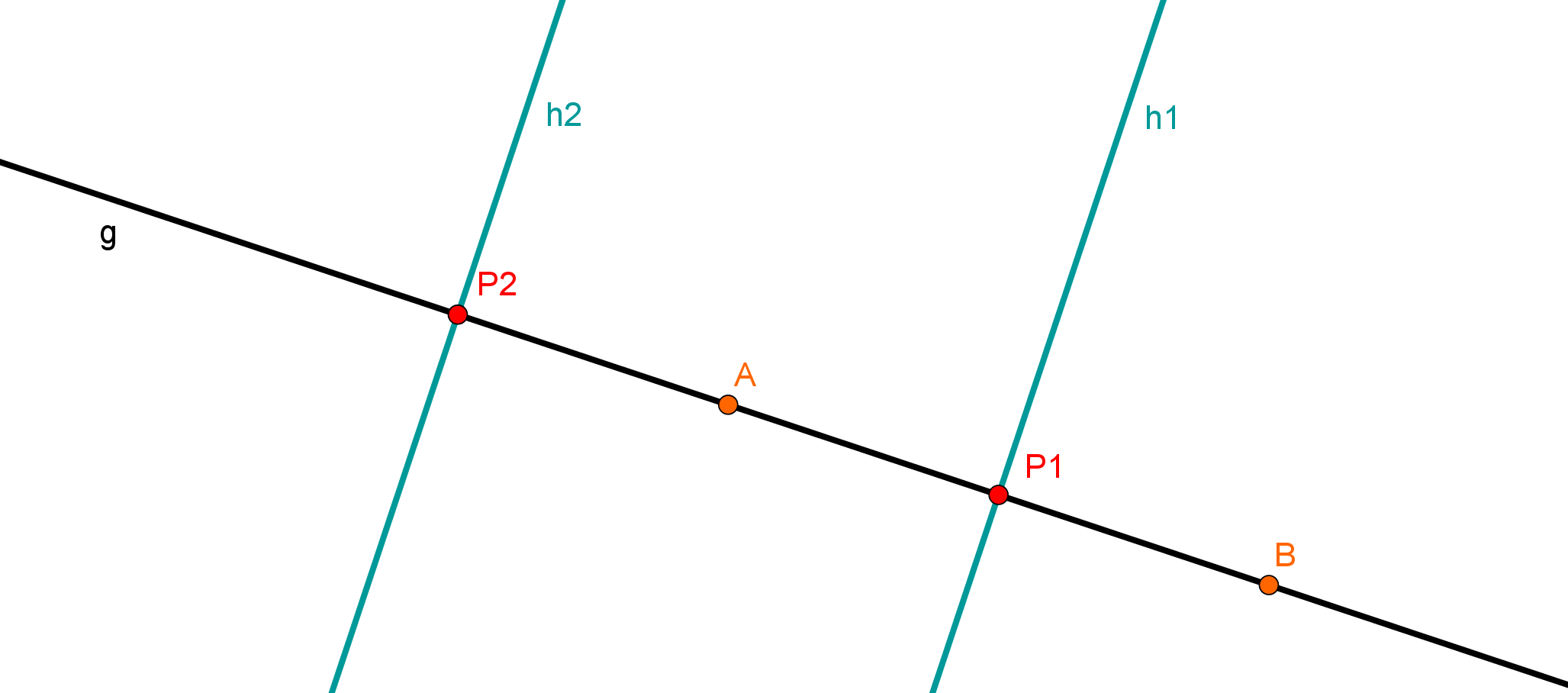
Normiere den Vektor , bringe ihn also zuerst auf die Länge .
Multipliziere diese Normierung mit , um den richtigen Abstand zu bekommen.
Nun kannst du den Stützpunkt der Geraden berechnen, indem du ihn zum Stützpunkt addierst bzw. von subtrahierst.
Die gesuchten Geraden sind also
