Gemischte Aufgaben zu linearen Funktionen - Geraden

…

123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann

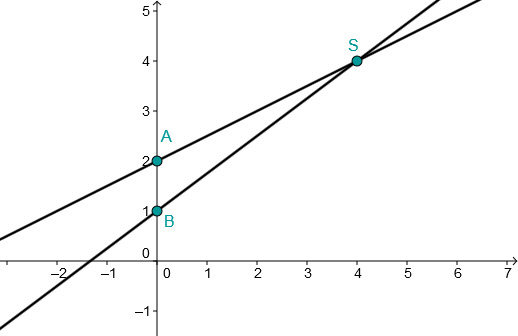
Geradenschnittpunkte berechnen.

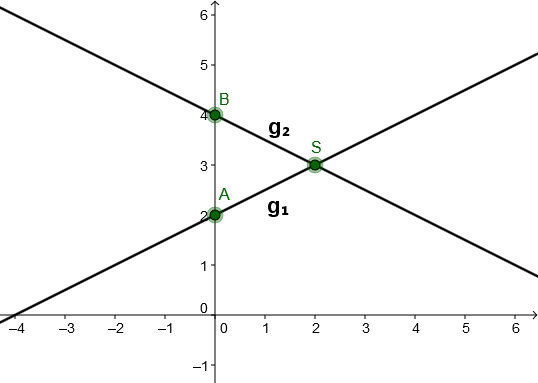
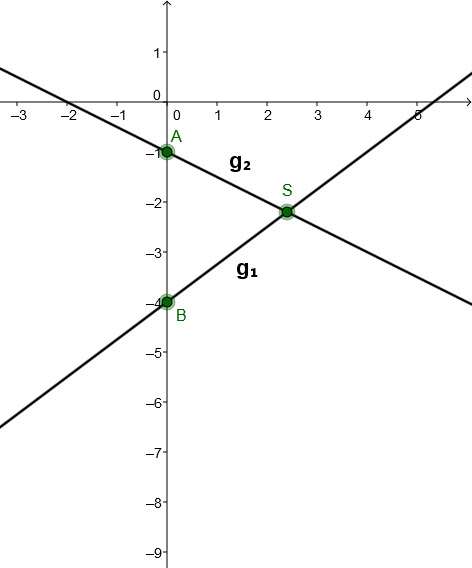
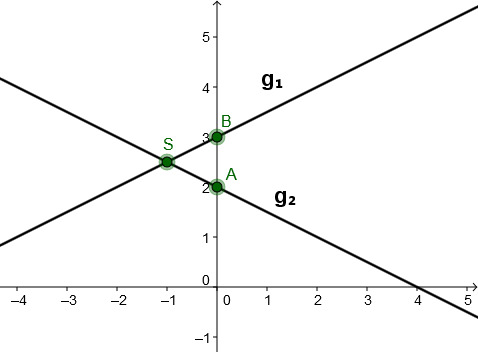
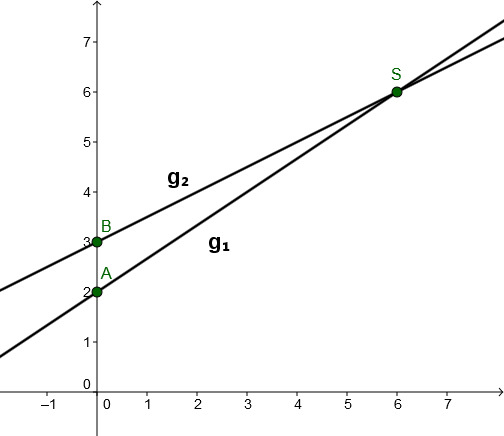
Gegeben sind die Funktionsgleichungen zweier Geraden $g_1(x)$ und $g_2\left(x\right)$ . Berechnen Sie den Schnittpunkt beider Geraden und zeichnen Sie die Geraden in ein Koordinatensystem.

Gib den Schnittpunkt in das Eingabefeld ein: "S(1;3)" oder S(1|3)" zum Beispiel.

${\mathrm g}_1\left(\mathrm x\right)=\frac12\mathrm x+2\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=-\frac12\mathrm x+4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen

Geradenschnittpunkte berechnen

Setze dafür $g_1(x)$ und $g_2(x)$ gleich.

$\displaystyle \frac12\mathrm x+2$	$=$	$\displaystyle -\frac12\mathrm x+4\\$	$\displaystyle \left\|+\frac12x-2\right.$
$\displaystyle \frac12\mathrm x+\frac12\mathrm x$	$=$	$\displaystyle 4-2$
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 2$
	↓	Setze x in ${\mathrm g}_1\left(\mathrm x\right)$ ein.
$\displaystyle \text{y}$	$=$	$\displaystyle 1+2$
$\displaystyle \mathrm y_S$	$=$	$\displaystyle 3$

$\Rightarrow\;\;\mathrm S\left(x_S|y_S\right)=\mathrm S\left(2|3\right)$

Zeichnung

Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

${\mathrm g}_1\left(\mathrm x\right)=2\mathrm x-1\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=-2\mathrm x+1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen

Geradenschnittpunkt berechnen

Setze ${\mathrm g}_1(\mathrm x)$ und ${\mathrm g}_2(\mathrm x)$ gleich.

$\displaystyle 2x-1$	$=$	$\displaystyle -2x+1$	$\displaystyle +2x+1$
$\displaystyle 2x+2x$	$=$	$\displaystyle 1+1$
$\displaystyle 4x$	$=$	$\displaystyle 2$	$\displaystyle :4$
$\displaystyle \mathrm x_S$	$=$	$\displaystyle \frac{1}{2}$
	↓	Setze x in ${\mathrm g}_1(\mathrm x)$ ein.
$\displaystyle y$	$=$	$\displaystyle 2\cdot\frac{1}{2}-1$
$\displaystyle y$	$=$	$\displaystyle 1-1$
$\displaystyle \mathrm y_S$	$=$	$\displaystyle 0$

$\Rightarrow\;\;\mathrm S\left(x_S|y_S\right)=\mathrm S\left(\frac12|0\right)$

$\Rightarrow\ \text{S}$ ist der Schnittpunkt der Geraden.

Zeichnung

Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

${\mathrm g}_1\left(\mathrm x\right)=\frac34\mathrm x-4\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=-\frac12\mathrm x-1$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen

Geradenschnittpunkt berechnen

Setze ${\mathrm g}_1(\mathrm x)$ und ${\mathrm g}_2(\mathrm x)$ gleich.

$\displaystyle g_1(x)$	$=$	$\displaystyle g_2(x)$
$\displaystyle \frac{3}{4}x-4$	$=$	$\displaystyle -\frac{1}{2}x-1$	$\displaystyle +\frac{1}{2}x+4$
$\displaystyle \frac{3}{4}x+\frac{1}{2}x$	$=$	$\displaystyle -1+4$
$\displaystyle 1{,}25x$	$=$	$\displaystyle 3$	$\displaystyle 1{,}25$
$\displaystyle x$	$=$	$\displaystyle \frac{3}{1{,}25}$
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 2{,}4$
	↓	Setze $x_S$ in ${\mathrm g}_1(\mathrm x)$ ein.
$\displaystyle y$	$=$	$\displaystyle \frac{3}{4}\cdot2{,}4-4$
$\displaystyle y$	$=$	$\displaystyle 1{,}8-4$
$\displaystyle \mathrm y_S$	$=$	$\displaystyle -2{,}2$

$\Rightarrow\;\;\mathrm S\left(x_S|y_S\right)=\mathrm S\left(2{,}4|-2{,}2\right)$

Zeichnung

Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

${\mathrm g}_1\left(\mathrm x\right)=-\frac12\mathrm x+2\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=\frac12\mathrm x+3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen

Geradenschnittpunkt berechnen

Setze ${\mathrm g}_1\left(\mathrm x\right)$ und ${\mathrm g}_2\left(\mathrm x\right)$ gleich.

$\displaystyle g_1\left(x\right)$	$=$	$\displaystyle g_2\left(x\right)$
$\displaystyle -\frac12\mathrm x+2$	$=$	$\displaystyle \frac12\mathrm x+3\\$	$\displaystyle \left\|+\frac12\mathrm x\right.-3$
$\displaystyle 2-3$	$=$	$\displaystyle \frac{1}{2}x+\frac{1}{2}x$
$\displaystyle \mathrm{x}_S$	$=$	$\displaystyle -1$
	↓	Setze $x_S$ in ${\mathrm g}_1\left(\mathrm x\right)$ ein.
$\displaystyle y$	$=$	$\displaystyle -\frac12\cdot\left(-1\right)+2\\$
$\displaystyle y$	$=$	$\displaystyle \frac{1}{2}+2$
$\displaystyle \mathrm{y}_S$	$=$	$\displaystyle 2{,}5$

$\Rightarrow\;\;\mathrm S(x_S|y_S)=\mathrm S\left(-1|2{,}5\right)$

$\Rightarrow\ S$ ist der Schnittpunkt der Geraden.

Zeichnung

Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

${\mathrm g}_1\left(\mathrm x\right)=\frac23\mathrm x+2\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=\frac12\mathrm x+3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen

Geradenschnittpunkt berechnen

Setze ${\mathrm g}_1\left(\mathrm x\right)$ und ${\mathrm g}_2\left(\mathrm x\right)$ gleich.

\displaystyle g_1(x)

=

\displaystyle g_2(x)

$\displaystyle \frac{2}{3}\mathrm{x}+2$	$=$	$\displaystyle \frac{1}{2}\mathrm{x}+3$	$\displaystyle -\frac{1}{2}\mathrm{x}-2$
$\displaystyle \frac{2}{3}\mathrm{x}-\frac{1}{2}\mathrm{x}$	$=$	$\displaystyle 3-2$
	↓	Bringe die Brüche auf den kleinsten gemeinsamen Nenner.
$\displaystyle \frac{4}{6}\mathrm{x}-\frac{3}{6}\mathrm{x}$	$=$	$\displaystyle 3-2$
$\displaystyle \frac{1}{6}x$	$=$	$\displaystyle 1$	$\displaystyle :\frac{1}{6}$
$\displaystyle x$	$=$	$\displaystyle \displaystyle\frac1{\frac16}$
	↓	Du dividierst durch einen Bruch $\rightarrow$ Multipliziere mit dem Kehrwert.
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 6$

Setze $x_S$ in ${\mathrm g}_1\left(\mathrm x\right)$ ein.

$\mathrm y=\frac23\cdot6+2\\$

$\mathrm y=4+2\\$

$\mathrm y_S=6$

$\Rightarrow\;\;\mathrm S(x_S|y_S)=\mathrm S\left(6|6\right)$

Zeichnung

Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

${\mathrm g}_1\left(\mathrm x\right)=\frac34\mathrm x+1\;\;\;\;\;{\mathrm g}_2\left(\mathrm x\right)=\frac12\mathrm x+2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen

Geradenschnittpunkt berechnen

Setze ${\mathrm g}_1\left(\mathrm x\right)$ und ${\mathrm g}_2\left(\mathrm x\right)$ gleich.

$g_1(x)=g_2(x)\\$

$\displaystyle \frac34\mathrm x+1$	$=$	$\displaystyle \frac12\mathrm x+2$	$\displaystyle -\frac12x-1$
$\displaystyle \frac34\mathrm x-\frac12\mathrm x$	$=$	$\displaystyle 2-1$
	↓	Bringe die Brüche auf den kleinsten gemeinsamen Nenner .
$\displaystyle \frac34\mathrm x-\frac24\mathrm x$	$=$	$\displaystyle 2-1$
$\displaystyle \frac14\mathrm x$	$=$	$\displaystyle 1$	$\displaystyle :\frac14$
$\displaystyle x$	$=$	$\displaystyle \displaystyle\frac1{\frac14}$
	↓	Du dividierst durch einen Bruch $\rightarrow$ Multipliziere mit dem Kehrwert.
$\displaystyle \mathrm x_S$	$=$	$\displaystyle 4$

Setze $x_S$ in ${\mathrm g}_1\left(\mathrm x\right)$ ein.

$\mathrm y=\frac34\cdot4+1\\$

$\mathrm y=3+1\\$

$y_S=4\\$

$\Rightarrow\;\;\mathrm S(x_S|y_S)=\mathrm S\left(4|4\right)$

$S$ ist der Schnittpunkt der Geraden

Zeichnung

Verbinde jeweils die y-Achsenabschnitte (hier A und B) mit dem berechneten Schnittpunkt S. Diese legen die Geraden eindeutig fest.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇