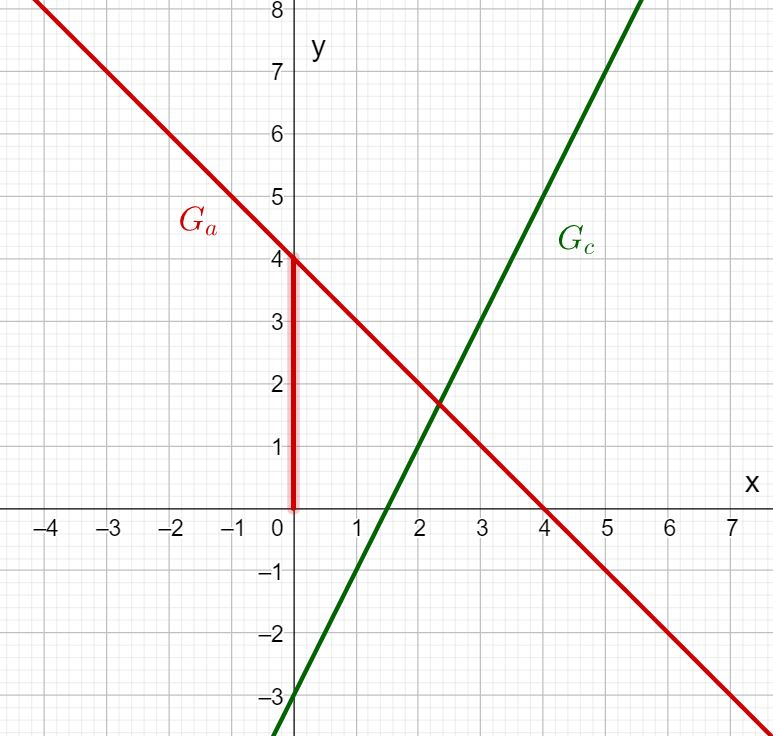
Betrachte die Graphen der Funktionen a(x) und c(x). Lies den y-Achsenabschnitt und die Steigung der Geraden ab und trage sie in die Felder ein! Kannst du daraus den Funktionsterm aufstellen?
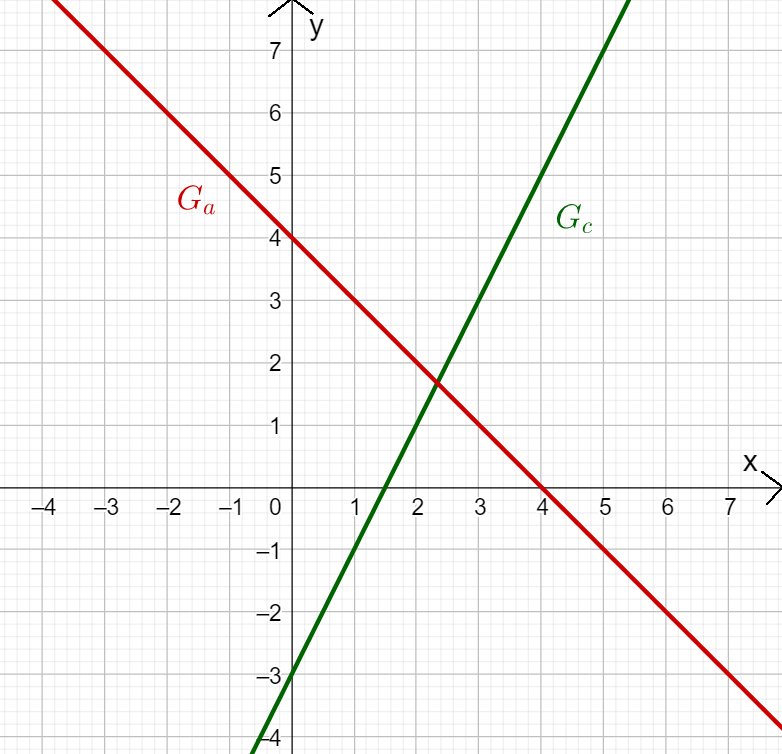
Welchen y-Achsenabschnitt hat a(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
y-Achsenabschnitt bestimmen
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Gerade mit der y-Achse betrachtest.
In diesem Fall:
Der y-Achsenabschnitt ist der y-Wert des Schnittpunkts (0/4), also 4.
Hast du eine Frage oder Feedback?
Achte darauf, wo die Gerade Ga die y-Achse schneidet.
Bestimme dann den Schnittpunkt!
Welche Steigung hat a(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Geraden
Steigung bestimmen
Die Steigung einer Geraden bestimmt man am einfachsten mithilfe eines Steigungsdreiecks.
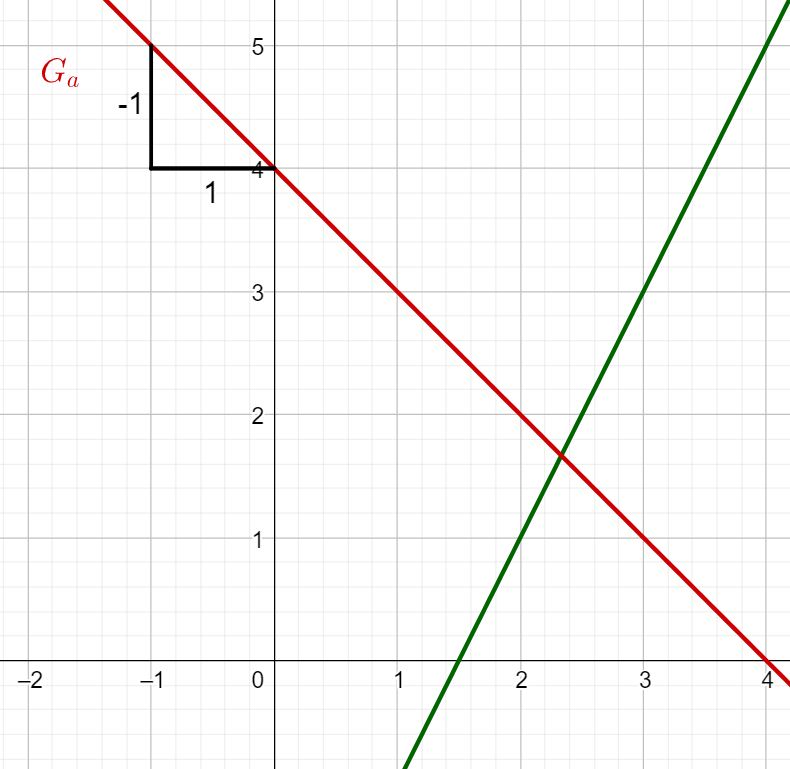
Im Fall von Ga:
Du kannst ablesen, dass du eine Längeneinheit nach unten und eine Längeneinheit nach rechts gehst.
Du erhältst für die Steigung: m=−1
Hast du eine Frage oder Feedback?
Kreiere dafür ein Steigungsdreieck (siehe unten).
Bestimme dann die Steigung.
Welchen Funktionsterm hat a(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Funktionsterm aufstellen
Der Funktionsterm einer linearen Funktion hat die Form:
y=mx+tDabei steht m für die Steigung und t für den y-Achsenabschnitt.
Setzt du die Werte aus den vorigen Teilaufgaben ein erhältst du:
y=−1⋅x+4Vereinfacht ist das:
y=−x+4Die Funktionsgleichung von Ga ist also:
a(x)=−x+4.
Hast du eine Frage oder Feedback?
Schau dir das Grundwissen zu der linearen Funktion an.
Setze deine bisherigen Werte in die Funktion ein (siehe unten für eine ausführlichere Erklärung).
Welchen y-Achsenabschnitt hat c(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geraden
y-Achsenabschnitt bestimmen
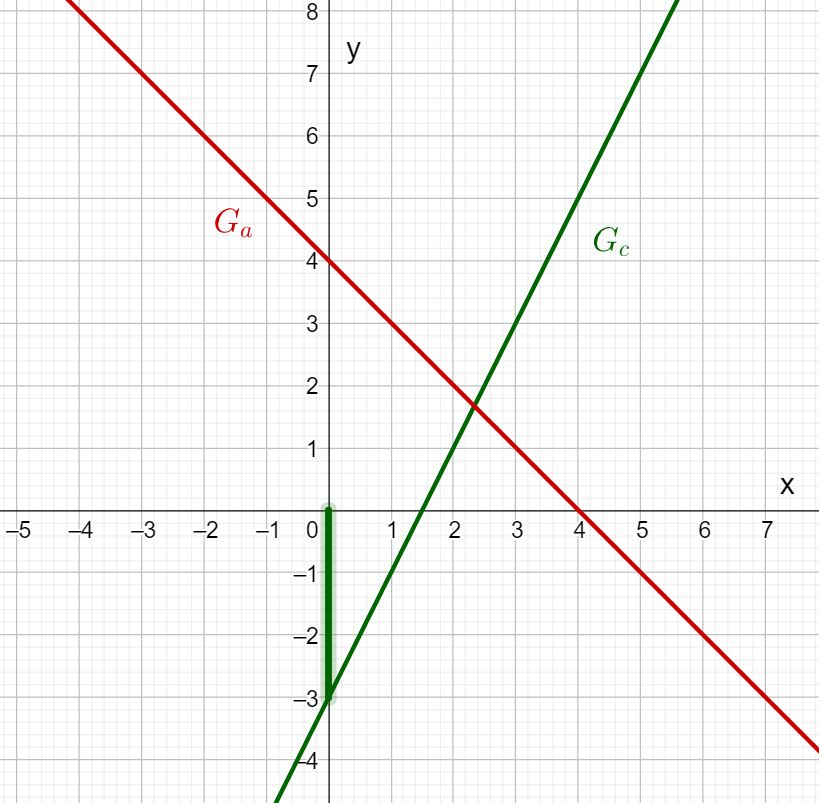
Den y-Achsenabschnitt bestimmst du, indem du den Schnittpunkt der Gerade mit der y-Achse betrachtest.
In diesem Fall:
Der y-Achsenabschnitt von Gc ist also −3.
Hast du eine Frage oder Feedback?
Achte darauf, wo die Gerade Gc die y-Achse schneidet.
Bestimme dann den Schnittpunkt!
Welche Steigung hat c(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung der Geraden
Steigung bestimmen
Die Steigung einer Geraden bestimmt man am einfachsten mithilfe eines Steigungsdreiecks.
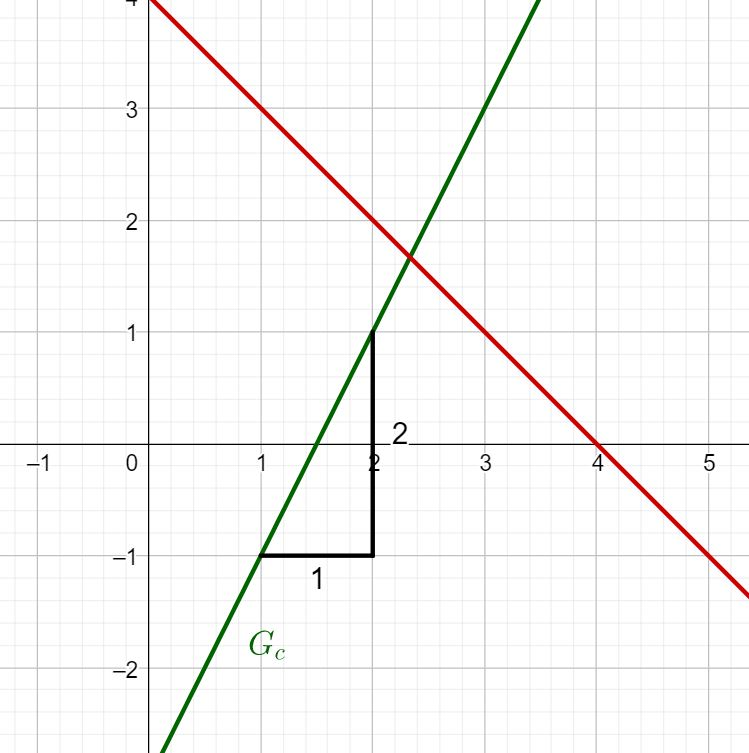
Im Fall von Gc:
Du kannst ablesen, dass du eine Längeneinheit nach rechts und zwei Längeneinheiten nach oben gehst.
Du erhältst für die Steigung: m=2
Hast du eine Frage oder Feedback?
Kreiere dafür ein Steigungsdreieck (siehe unten).
Bestimme dann die Steigung.
Welchen Funktionsterm hat c(x)?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Funktionsterm aufstellen
Der Funktionsterm einer linearen Funktion hat die Form:
y=mx+tDabei steht m für die Steigung und t für den y-Achsenabschnitt.
Setzt du die Werte aus den vorigen Teilaufgaben ein erhältst du:
y=2⋅x−3Die Funktionsgleichung von Gc ist also:
c(x)=2x−3Hast du eine Frage oder Feedback?
Schau dir das Grundwissen zur linearen Funktion an.
Setze deine bisherigen Werte in die Funktion ein (siehe unten für eine ausführlichere Erklärung).
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
