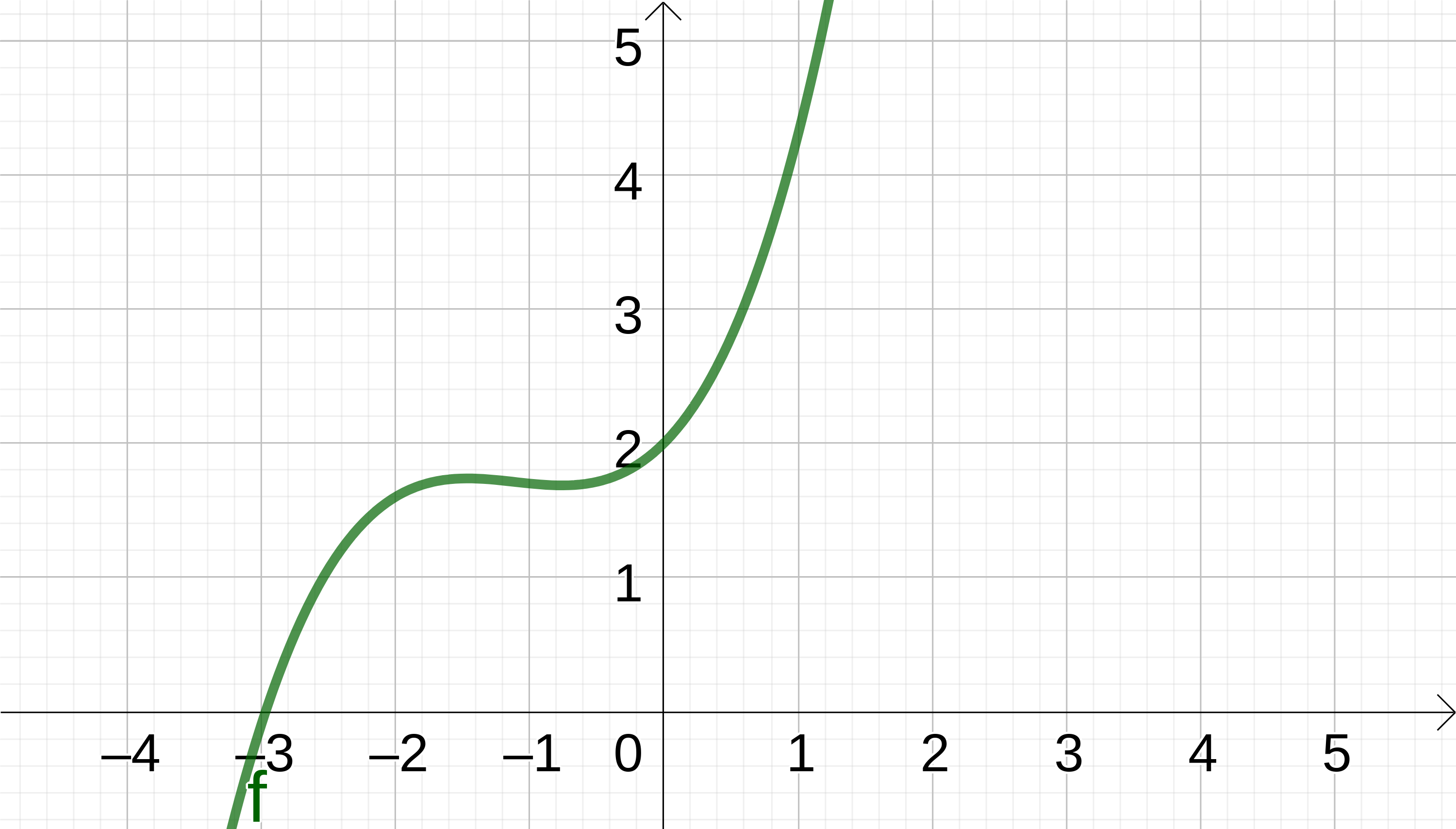
Zuerst einmal solltest du dir den Graphen anschauen. Um die Wertemenge herauszufinden musst du dir die/den höchsten bzw. niedrigsten klar definierbaren Punkt auf dem Graphen anschauen.

In diesem Fall geht der Graph in beide Richtungen ins Unendliche. Somit kannst du die angegebene Lösung $\;$ $W_f=\left] - \infty;2 \right ]$ ausschließen.

Jetzt musst du nur noch darauf achten, dass die Wertemenge richtig aufgeschrieben ist. Die eckigen Klammern müssen beim Unendlichkeitszeichen nach außen zeigen, da diese nicht begrenzt werden kann.

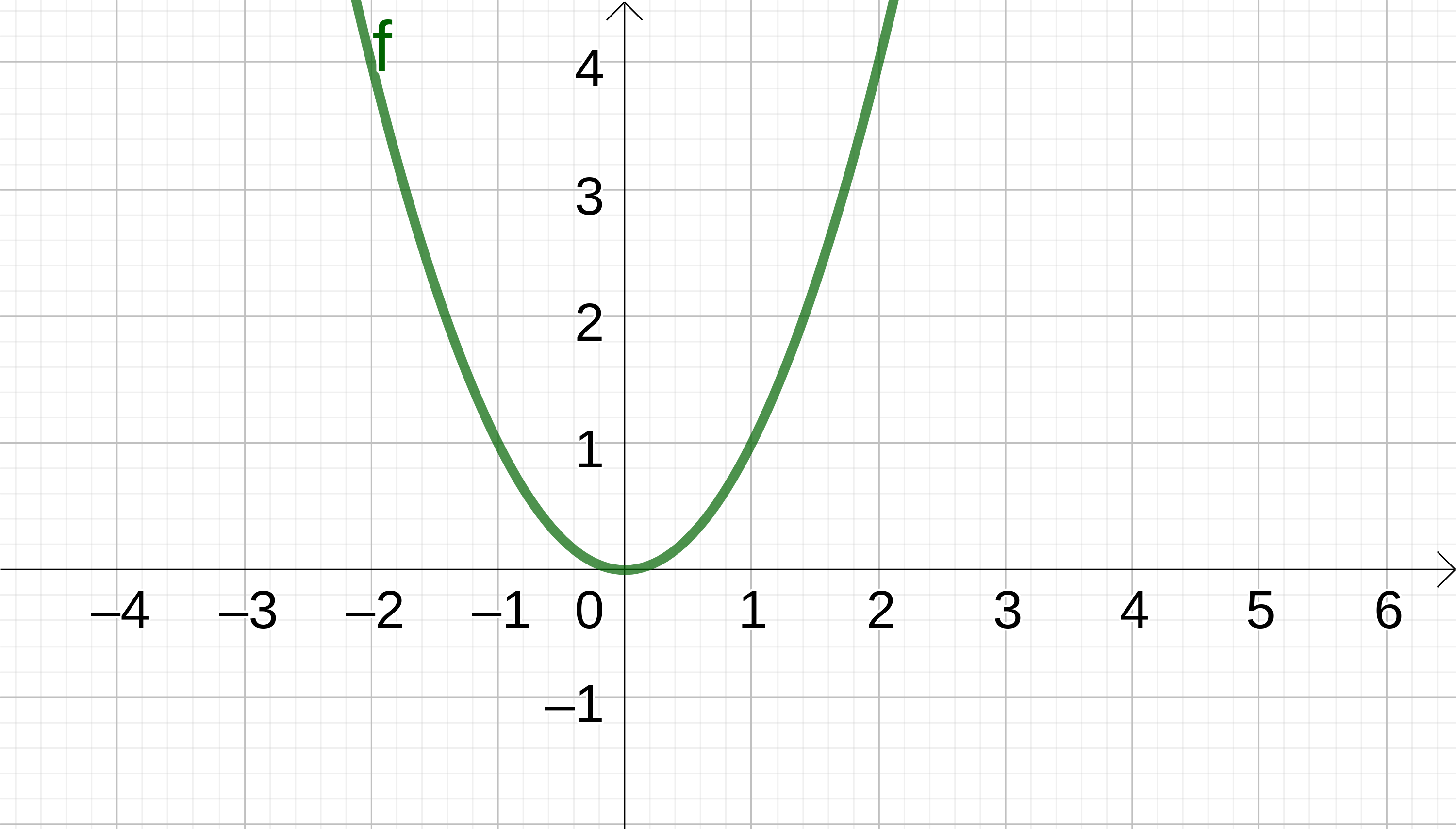
Betrachtest du den Graphen $f(x)$, wirst du bemerken, dass er einen tiefsten Punkt hat und deshalb nicht in die negative Unendlichkeit gehen kann. Der tiefste Punkt ist auf der y-Achste bei 0.

Nach oben hin lässt sich jedoch kein klar definierbarer höchster Punkt erkennen, folglich geht der Graph hier in die positive Unendlichkeit.

Wenn man nun diese Erkenntnisse kombiniert lässt sich sagen, dass die y-Werte von $f(x)$ minimal 0 und maximal $\infty$ erreichen.

Daher gilt für die Wertemenge: $W_f=\left] 0; \infty \right]$

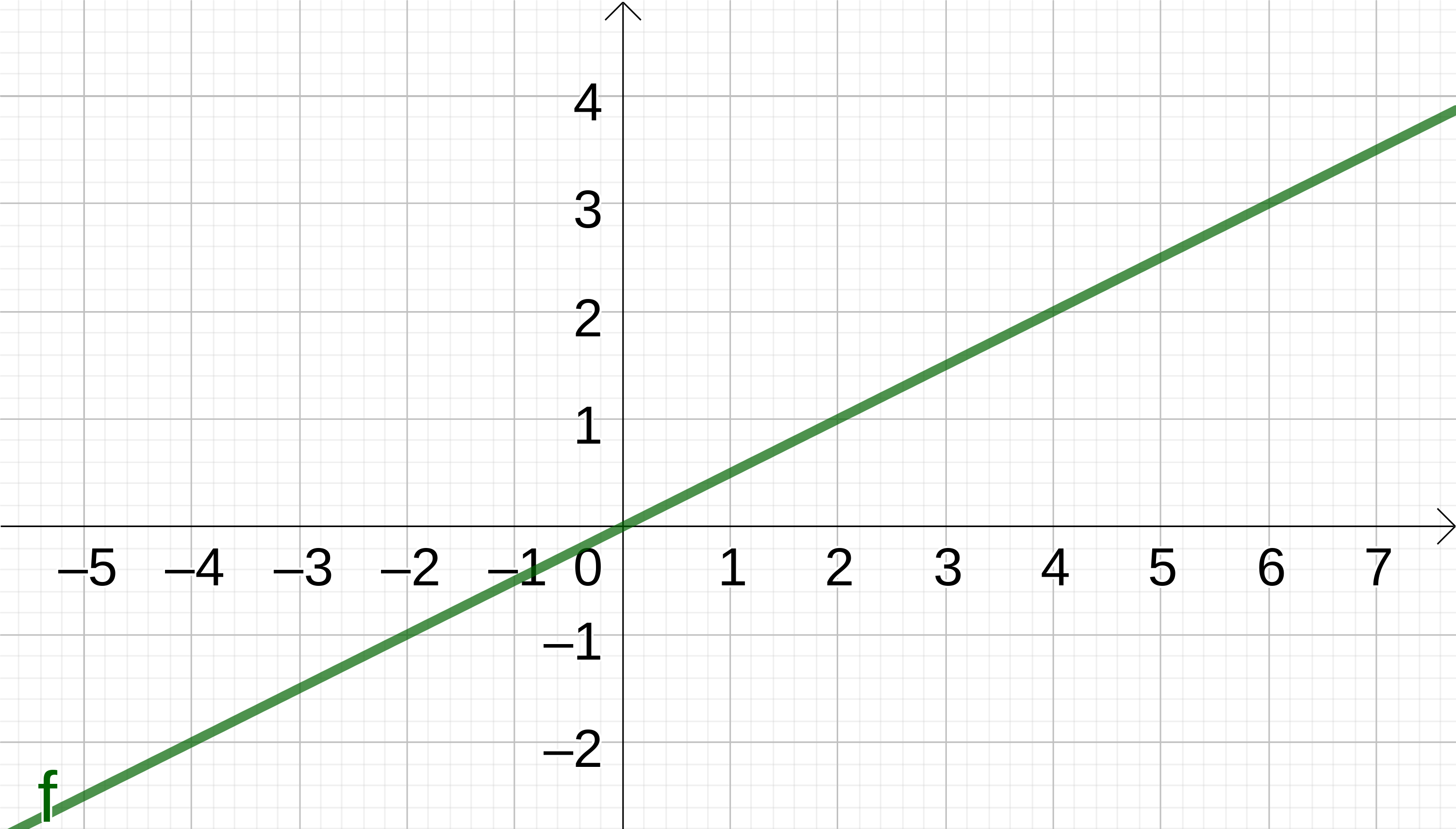
Da $x\in \mathbb{R}$ gilt, solltest du dir die y-Werte für alle x-Werte ansehen. Weil bspw. bei x=4, y=2 entspricht, lässt sich die Lösung $W_f=[-1;1 \ ]$ schonmal nicht mit dem Graphen von $f(x)$ verbinden.

Aber da der Graph nicht nur in die negative Unendlichkeit geht, sondern auch in die positive, gilt: $W_f=\left] - \infty; \infty \right [$