Gib den maximal möglichen Definitionsbereich an und untersuche das Verhalten des Graphen an den Definitionslücken sowie für . Skizziere den Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
↓ Untersuche, wann der Nenner null wird
↓ Schließe die Definitionslücken aus und bestimme so den Definitionsbereich
↓ Untersuche das Verhalten der Funktion an der 1. Definitionslücke
↓ Untersuche das Verhalten der Funktion an der 2. Definitionslücke
↓ Untersuche das Verhalten der Funktion im Unentlichen (Klammere dazu aus)
Skizze
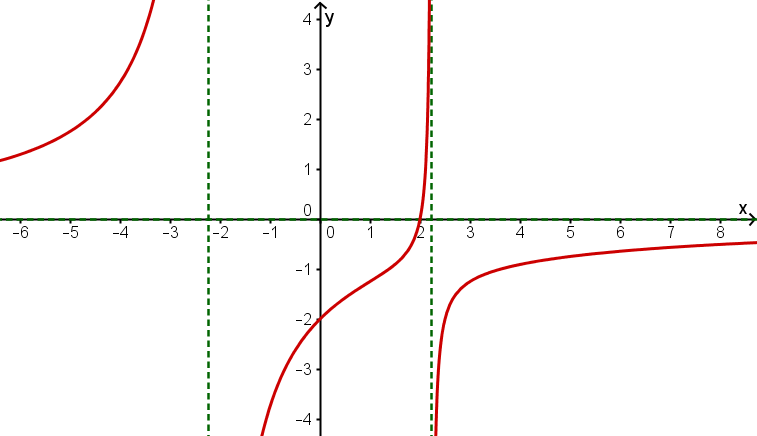
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
↓ Schließe die Definitionslücke aus und bestimme so den Definitionsbereich
↓ Bestimme das Verhalten der Funktion an der Definitionslücke
↓ Untersuche das Verhalten im Unendlichen. Da der Zählergrad, der Funktion größer ist als der Nennergrad, gibt es eine schräge Asymptote.
↓ Bestimme diese Asymptote durch Polynomdivision.
↓ Gib die schräge Asymptote an, da diese das Verhalten der Funktion im Unendlichen beschreibt.
Asymptote:
Skizze
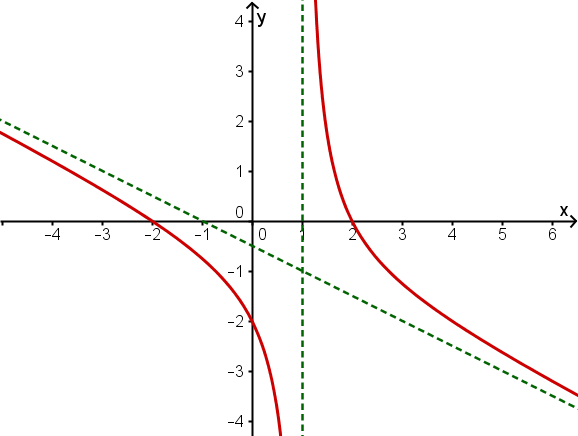
Hast du eine Frage oder Feedback?
Bestimme die Definitionlücken, indem zu schaust, wann der nenner 0 wird.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
Nenner: wird nie 0
keine Definitionslücke
Bestimme den Definitionsbereich
Bestimme das Verhalten der Funktion
Die Funktion besteht nicht nur aus einem Bruch, sondern hat davor noch einen linearen Term.
Die Funktion hat eine schräge Asymptote.
Bestimme diese. (kann direkt abgelesen werden)
Asymptote:
Skizze
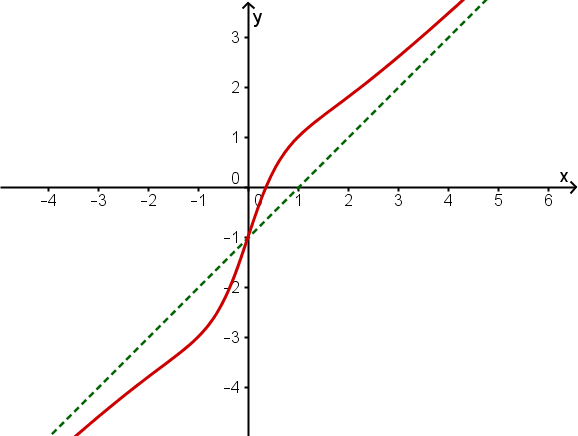
Hast du eine Frage oder Feedback?
Prüfe, ob der Nenner 0 wird.
Bestimme die Definitionslücken, indem du überprüfst, wann die Nenner 0 werden.
Schließe die beiden Definitionslücken aus und bestimme so den Definitionsbereich
↓ Fasse die beiden Brüche zu einem Bruch zusammen
↓ Da der Zählergrad größer ist, als der Nennergrad, gibt es eine schräge Asymptote. Bestimme diese Asymptote durch Polynomdivision .
Lese aus dieser Form die Asymptote direkt ab. Die Asymptote definiert das verhalten der Funktion im Unendlichen (Sie nähert sich er Asymptote an)
Asymptote:
Bestimme das Verhalten der Funktion an der 1. Definitionslücke
Bestimme das Verhalten der Funktion an der 2. Definitionslücke
Skizze
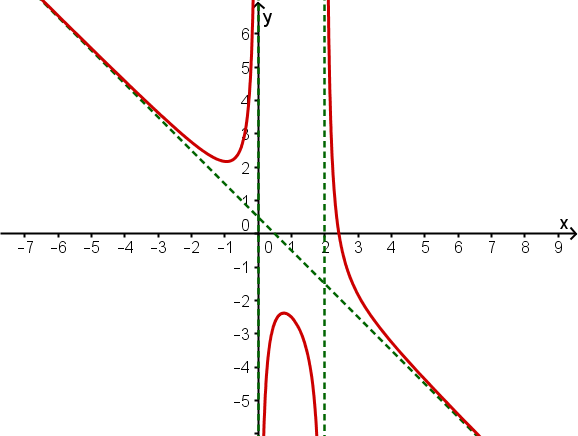
Hast du eine Frage oder Feedback?
Bestimme die Definitionslücken, indem du schaust, wann der Nenner 0 wird
Schließe die Definitionslücken aus und bestimme so den Definitionsbereich
Bestimme die beiden Grenzwerte (von links und von rechts) an der 1.Definitionslücke
Bestimme die beiden Grenzwerte an der 2.Definitionslücke
Bestimme das Verhalten der Funktion im Unendlichen. (Bestimme den Grenzwert im Unendlichen)
↓ Klammere im Zähler und im Nenner aus.
↓ Berechne den Grenzwert
Was bedeutet das für das Verhalten im Unendlichen?
Beidseitige Asymptote bei
Skizze
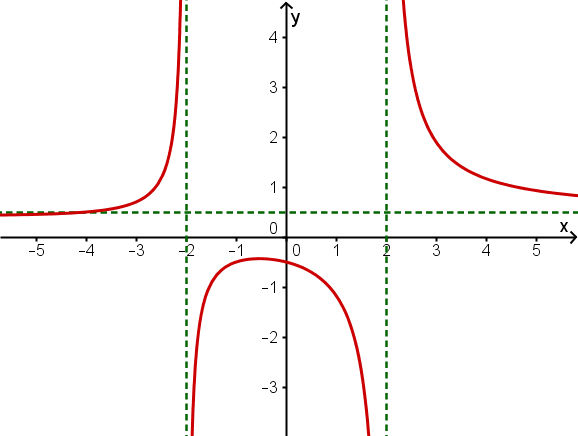
Hast du eine Frage oder Feedback?
Bestimme die Definitionslücken, indem du schaust, wann der Nenner 0 wird.
Betrachte die beiden Faktoren getrennt
Schließe die Definitionslücken aus und bestimme so den Definitionsbereich
Bestimme das Verhalten der Funktion an der 1.Definitionslücke. Bestimme dazu die beiden Grenzwerte, die sich von unten bzw. oben an diese annähern.
Bestimme das Verhalten der Funktion an der 2.Definitionslücke
↓ Forme den Term mit Polynomdivision um
Lese aus dieser Form die Asymptote direkt ab und gib sie an.
Asymptote bei
Skizze
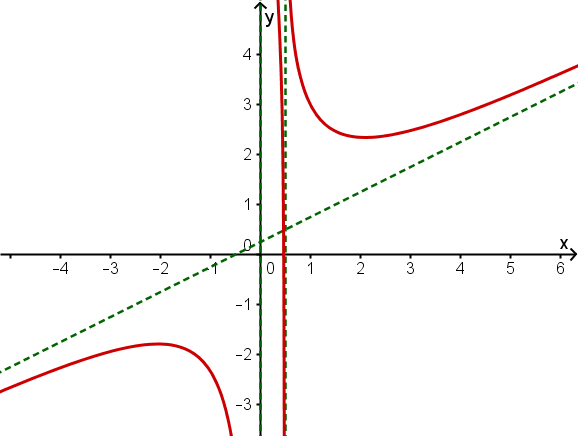
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?
