Lineare Gleichungssysteme, Inzidenzgeometrie
Bestimmen Sie die Lösungsmenge des Linearen Gleichungssystems.
Stellen Sie den Vektor als Linearkombination der drei Vektoren
, und dar.
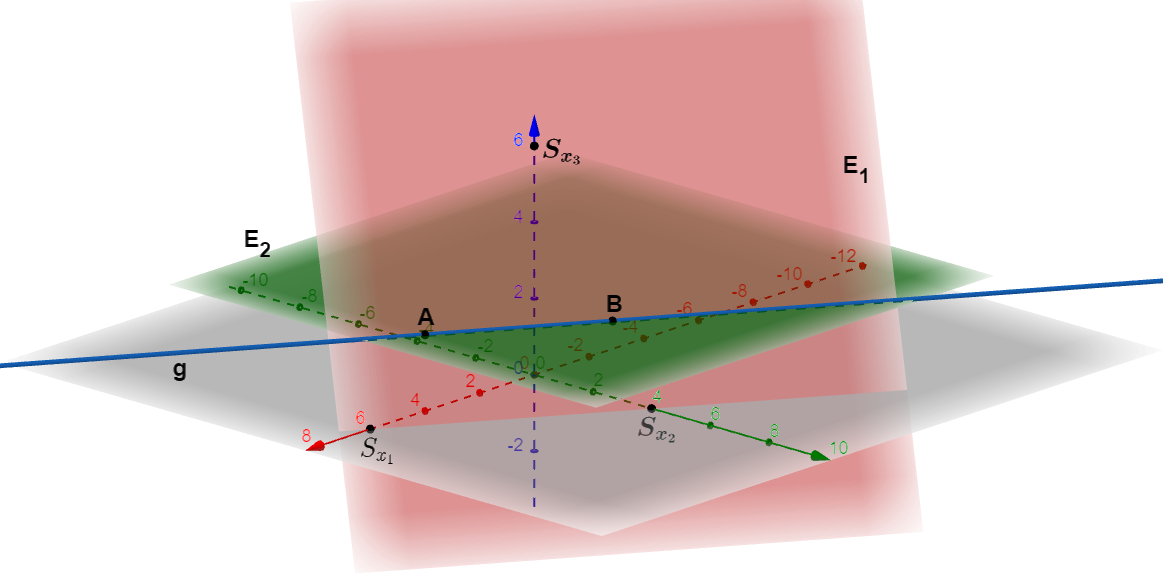
Gegeben sind die Ebenen und
a) Stellen Sie die Ebenen und in einem gemeinsamen Koordinatensystem dar.
b) Zeichnen Sie die Schnittgerade von und ein und bestimmen Sie die Gleichung der Schnittgeraden.
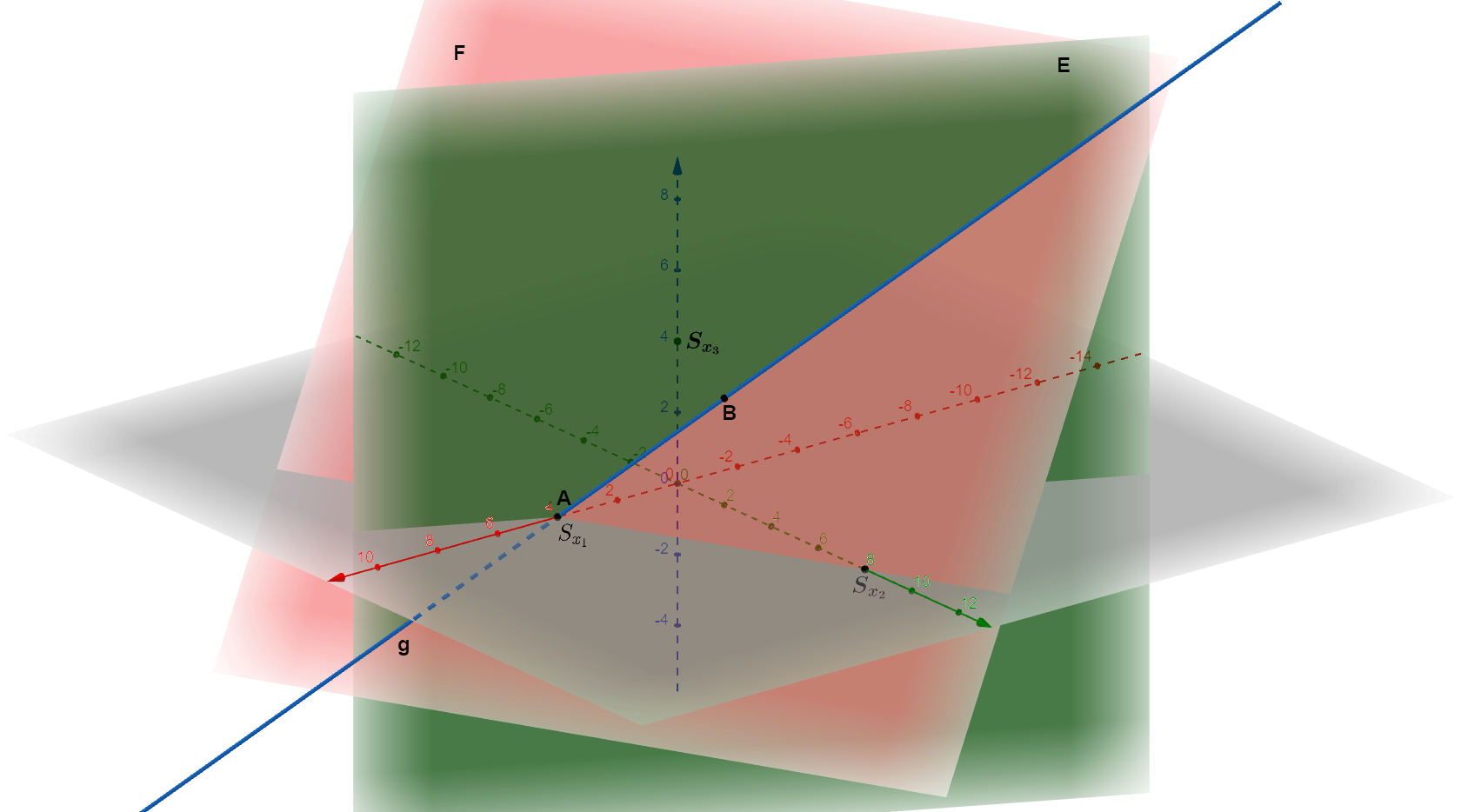
Gegeben sind die Ebenen und
a) Stellen Sie die Ebenen und in einem gemeinsamen Koordinatensystem dar.
b) Zeichnen Sie die Schnittgerade von und ein und bestimmen Sie die Gleichung der Schnittgeraden.
a) Geben Sie die Gleichung der Ebene an, welche die Spurpunkte und und keinen Schnittpunkt mit der -Achse hat.
b) Geben Sie die Gleichung der Ebene an, welche den Punkt ) enthält und parallel zur Ebene ist.
c) Geben Sie die Gleichung der Geraden an, welche durch den Punkt geht und senkrecht zur Ebene
steht.
Gegeben sind die Geraden und mit und
a) Zeigen Sie, dass und parallel, aber nicht identisch sind.
b) Geben Sie eine Gleichung der Ebene an, in der die Geraden und liegen.
Dieses Werk steht unter der freien Lizenz
CC BY 4.0 mit Namensnennung Landesbildungsserver Baden-Württemberg → Was bedeutet das?