🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

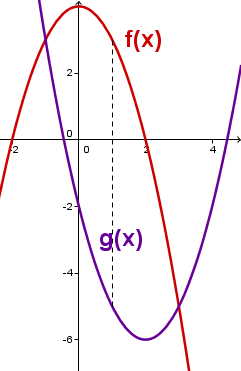
Gegeben sind die beiden Parabeln mit den Funktionsgleichungen

f(x)=4−x2\mathrm{f}(\mathrm{x})=4-\mathrm{x}^2   und  g(x)=(x−2)2−6\mathrm g(\mathrm x)=\left(\mathrm x-2\right)^2-6

  1. Zeichne die beiden Graphen sauber in ein Koordinatensystem

  2. Berechne die Schnittpunkte der beiden Parabeln

  3. Zeichnet man im Bereich −1<x<3-1<x<3 senkrechte Verbindungsstrecken von der oberen zur unteren Parabel, so haben diese Strecken unterschiedliche Längen.

    Bestimme die Strecke mit der größten Länge!  Zeichne diese Strecke in dein Bild ein!