Zeigen Sie, dass $f(x)$ zu jedem der drei Terme äquivalent ist: (4 BE)

$\frac{2}{(x+1)(x+3)}; \frac{2}{x^2+4x+3}; \frac{1}{0{,}5 \;\cdot (x+2)^2 -0{,}5}$

Begründen Sie, dass die x-Achse horizontale Asymptote von $G_f$ist, und geben Sie die Gleichungen der vertikalen Asymptoten von $G_f$ an. Bestimmen Sie die Koordinaten des Schnittpunkts von $G_f$ mit der y-Achse. (3 BE)

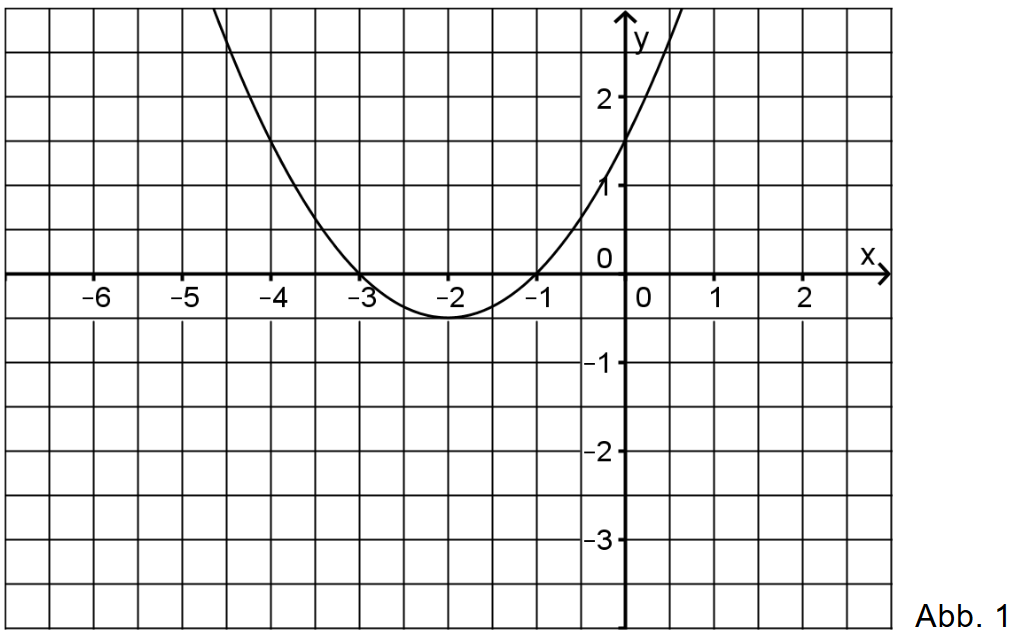
Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion

$p:x \mapsto 0{,}5 \cdot (x+2)^2 -0{,}5$, die die Nullstellen $x=-3\;$ und $x=-1$ hat.

Für $x \in \mathbb{D}_f$ gilt $f(x)=\frac{1}{p(x)}$.

Gemäß der Quotientenregel gilt für die Ableitungen $f'$ und $p'$ die Beziehung $f'(x)=-\frac{p'(x)}{(p(x))^2}$ für $x \in \mathbb{D}_f$.

Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von $f'(x)$ und $p'(x)$, dass $x=-2$ einzige Nullstelle von $f'$ ist und dass $G_f$ in $\left]-3;-2 \right[$ streng monoton steigend sowie in $\left]-2;-1 \right[$ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von $G_f$ an. (5 BE)

Berechnen Sie $f(-5)$ und $f(-1{,}5)$ und skizzieren Sie $G_f$ unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1. (4 BE)