Geometrie, Teil A, Aufgabengruppe 2

Die Vektoren $\vec{a} = (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})$ , $\vec{b} = (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array})$ und ${\vec{c}}_{t} = (\begin{array}{c} 4 t \\ 2 t \\ - 5 t \end{array})$ spannen für jeden Wert von $t \in ℝ ∖ {0}$ einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von $t$ .

Zeigen Sie, dass die aufgespannten Körper Quader sind. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorprodukt
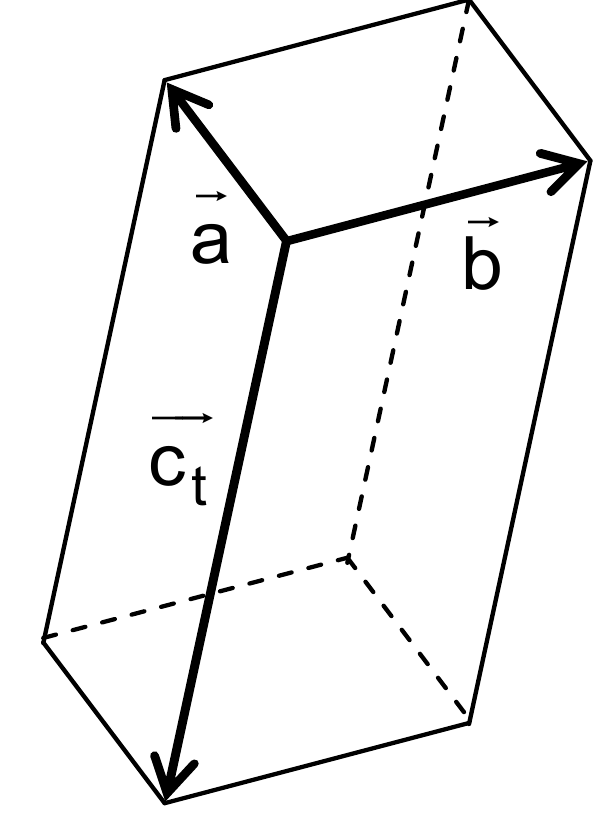
Zum Thema senkrecht sollten Dir zwei Dinge einfallen: Skalarprodukt und Vektorprodukt!
Lösungsmöglichkeit 1
Die Vektoren stehen aufeinander senkrecht, wenn deren Skalarprodukt $0$ ist. Zeige also mit dem Skalarprodukt, dass
$\vec{a} ⟂ \vec{b}$ ,
$\vec{b} ⟂ {\vec{c}}_{t}$ und
${\vec{c}}_{t} ⟂ \vec{a}$
zu 1.
$\vec{a} \circ \vec{b} = (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) \circ (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array}) = 2 \cdot (- 1) + 1 \cdot 2 + 2 \cdot 0 = - 2 + 2 + 0 = 0$
$\Rightarrow \vec{a} ⟂ \vec{b}$
zu 2.
$\vec{b} \circ {\vec{c}}_{t} = (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array}) \circ (\begin{array}{c} 4 t \\ 2 t \\ - 5 t \end{array}) = (- 1) \cdot 4 t + 2 \cdot 2 t + 0 \cdot (- 5 t) = - 4 t + 4 t + 0 = 0$
$\Rightarrow \vec{b} ⟂ \vec{c_{t}}$
zu 3.
${\vec{c}}_{t} \circ \vec{a} = (\begin{array}{c} 4 t \\ 2 t \\ - 5 t \end{array}) \circ (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) = 4 t \cdot 2 + 2 t \cdot 1 + (- 5 t) \cdot 2 = 8 t + 2 t - 10 t = 0$
$\Rightarrow \vec{c_{t}} ⟂ \vec{a}$
Weil alle Vektoren aufeinander senkrecht stehen, ist der obige Körper ein Quader.
Lösungsmöglichkeit 2
Bestimme wie in Lösungsmöglichkeit 1
das Skalarprodukt von $\vec{a}$ und $\vec{b}$ und zeige, dass die beiden Vektoren aufeinander senkrecht stehen.
Berechne danach das Vektorprodukt von $\vec{a}$ und $\vec{b}$ und zeige, dass der berechnete Vektor ein Vielfaches von ${\vec{c_{t}}}_{}$ ist .
$\vec{a} \circ \vec{b} = 0$ (wie oben gezeigt)
$\begin{array}{ccc} \vec{a} \times \vec{b} & = & (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) \times (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array}) \\ = & (\begin{array}{c} 1 \cdot 0 - 2 \cdot 2 \\ 2 \cdot (- 1) - 2 \cdot 0 \\ 2 \cdot 2 - 1 \cdot (- 1) \end{array}) \\ = & (\begin{array}{c} - 4 \\ - 2 \\ 5 \end{array}) \\ = & \frac{1}{t} \cdot \vec{c_{t}} \end{array}$
Der Ergebnisvektor ist bis auf ein Vielfaches gleich dem Vektor ${\vec{c}}_{t}$ , also handelt es sich bei dem zu untersuchenden Körper um einen Quader!
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Bestimmen Sie diejenigen Werte von $t$ , für die der jeweils zugehörige Quader das Volumen 15 besitzt. (3BE)

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

	$(\vec{a} \times \vec{b}) \cdot \vec{c}$
$=$	$(\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) \times (\begin{array}{c} - 1 \\ 2 \\ 0 \end{array}) \cdot (\begin{array}{c} 4 t \\ 2 t \\ - 5 t \end{array})$
	↓ Kreuzprodukt bilden
$=$	$(\begin{array}{c} (0 - 4) \\ (- 2 - 0) \\ (4 + 1) \end{array}) \cdot (\begin{array}{c} 4 t \\ 2 t \\ - 5 t \end{array})$
$=$	$(\begin{array}{c} - 4 \\ - 2 \\ 5 \end{array}) \cdot (\begin{array}{c} 4 t \\ 2 t \\ - 5 t \end{array})$
	↓ Skalarprodukt berechnen
$=$	$- 4 \cdot 4 t + (- 2) \cdot 2 t + 5 \cdot (- 5 t)$
$=$	$- 16 t - 4 t - 25 t$
$=$	$- 45 t$

	$\| \vec{a} \|$
$=$	$\sqrt{(a_{1})^{2} + (a_{2})^{2} + (a_{3})^{2}}$
$=$	$\sqrt{2^{2} + 1^{2} + 2^{2}}$
$=$	$\sqrt{4 + 1 + 4}$
$=$	$\sqrt{9}$
$=$	$3$

	$\vec{b}$
$=$	$\sqrt{(b_{1})^{2} + (b_{2})^{2} + (b_{3})^{2}}$
$=$	$\sqrt{(- 1)^{2} + 2^{2} + 0^{2}}$
$=$	$\sqrt{1 + 4}$
$=$	$\sqrt{5}$

	$\| \vec{c} \|$
$=$	$\sqrt{(c_{1})^{2} + (c_{2})^{2} + (c_{3})^{2}}$
$=$	$\sqrt{(4 t)^{2} + (2 t)^{2} + (- 5 t)^{2}}$
$=$	$\sqrt{16 t^{2} + 4 t^{2} + 25 t^{2}}$
$=$	$\sqrt{45 t^{2}}$
	↓ Die Wurzel eines Quadrats ist der Betrag
$=$	$\sqrt{45} \| t \|$

$15$	$=$	$\| \vec{a} \| \cdot \| \vec{b} \| \cdot \| \vec{c} \|$
$15$	$=$	$3 \cdot \sqrt{5} \cdot \sqrt{45} \| t \|$	$/ 3$
$5$	$=$	$\sqrt{5} \cdot \sqrt{45 t^{2}}$
	↓	$5 \cdot 45 = 255 = 15^{2}$
$5$	$=$	$15 \| t \|$
$\frac{1}{3}$	$=$	$\| t \|$

Lösungsmöglichkeit 1

Lösungsmöglichkeit 2

Hast du eine Frage oder Feedback?

Lösungsmöglichkeit 1: Das Spatprodukt

Lösungsmöglichkeit 2: Länge der Vektoren

Hast du eine Frage oder Feedback?