Trapeze rotieren um die Achse . Die Winkel haben das Maß mit .
Es gilt: ; ; .
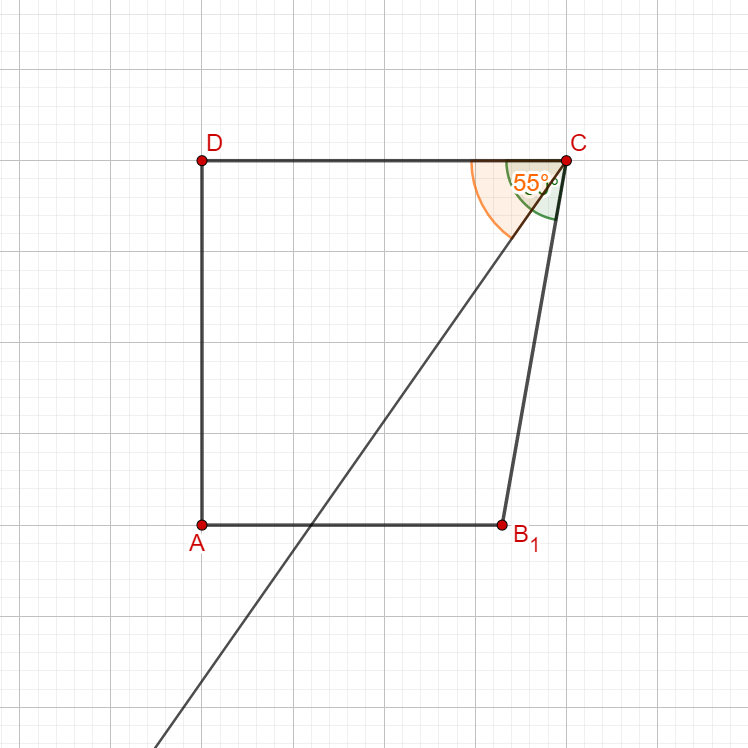
Die Zeichnung zeigt das Trapez für .
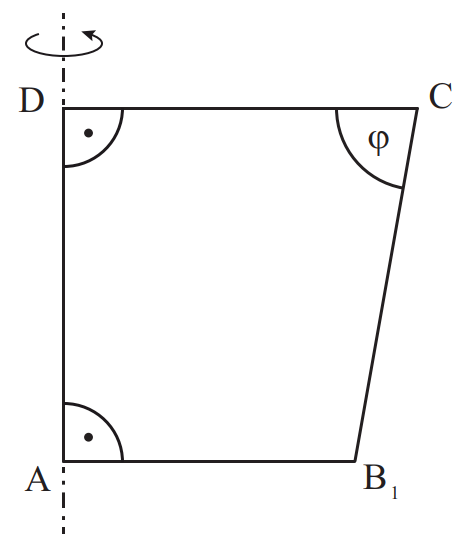
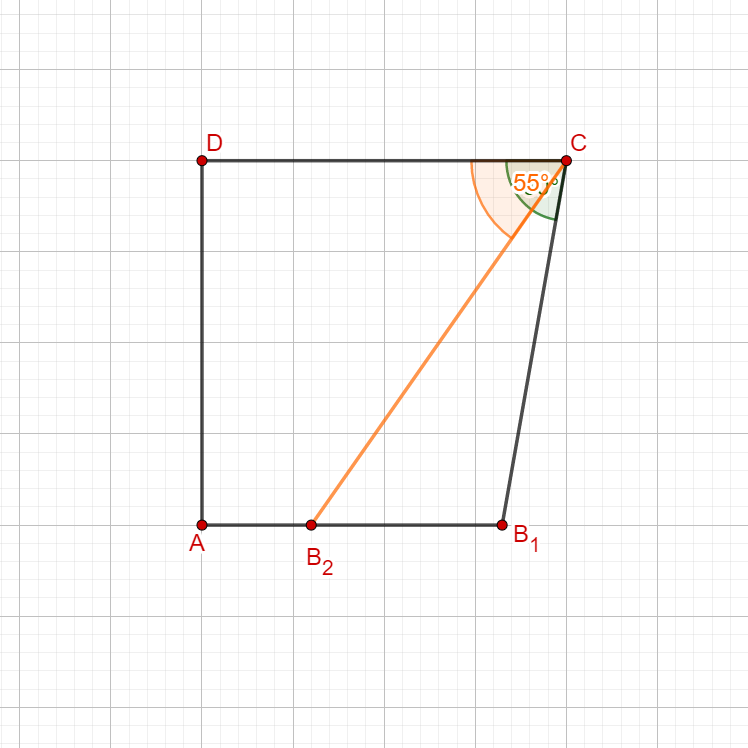
Zeichnen Sie das Trapez für in die Zeichnung ein.
(1 Punkt)
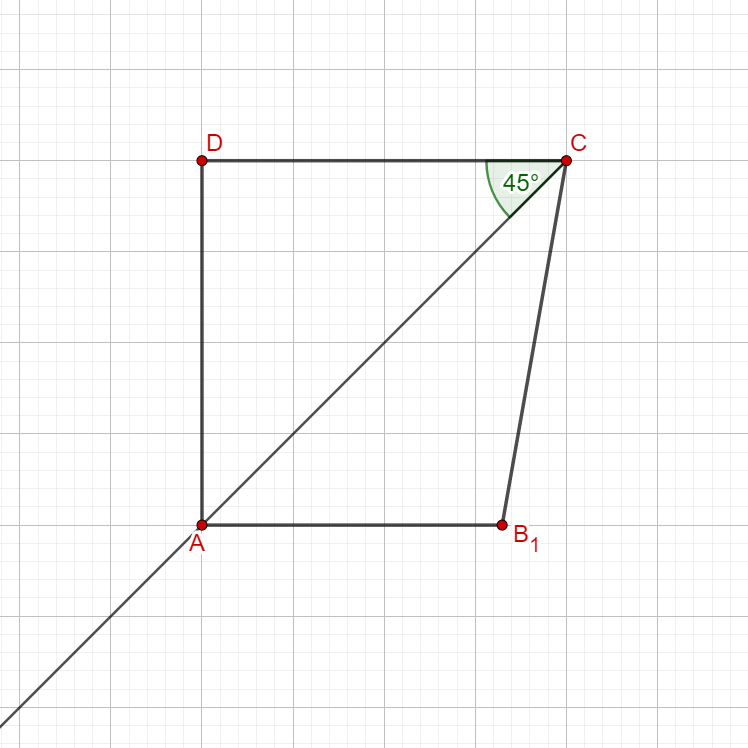
Bestätigen Sie die untere Intervallgrenze für und begründen Sie sodann, dass das Volumen der Rotationskörper gilt: .
(2 Punkte)
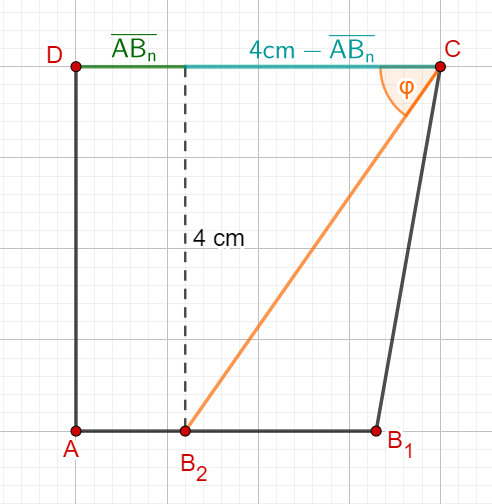
Zeigen Sie, dass für die Länge der Strecken in Abhängigkeit von gilt:
(2 Punkte)