Aufgaben zu Kugeln und Geraden

Gegeben sind eine Kugel $K$ mit Mittelpunkt $M (1 ∣ 2 ∣ 3)$ , Radius $r=\sqrt{10}$ und eine Gerade $g:\;\vec X=\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\y \\ 4\end{pmatrix}$ .

Für welchen Wert von $y$ ist die Gerade $g$ eine Tangente an die Kugel $K$ ? Gib auch den Berührpunkt an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel und Geraden

Aufstellen der Kugelgleichung

$\textcolor{ff6600}{M(1|2|3)}$ , $\textcolor{006400}{r=\sqrt{10}}$

$K:\ (\vec{x}-\textcolor{ff6600}{\vec{m}})^2=\textcolor{006400}{r^2}$

$K:\ \left(\vec x-\textcolor{ff6600}{\begin{pmatrix}1\\2\\3\end{pmatrix}}\right)^2=\left(\textcolor{006400}{\sqrt{10}}\right)^2=10$

Setze die Gleichung der Geraden für den Vektor $\vec x$ in die Kugelgleichung ein.

$g:\;\vec X=\textcolor{660099}{\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\y \\ 4\end{pmatrix}}$ in $K:\ \left(\vec x-\textcolor{ff6600}{\begin{pmatrix}1\\2\\3\end{pmatrix}}\right)^2=10$ einsetzen:

$\displaystyle \left(\textcolor{660099}{\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\y \\ 4\end{pmatrix}}-\textcolor{ff6600}{\begin{pmatrix}1\\2\\3\end{pmatrix}}\right)^2$	$=$	$\displaystyle 10$
	↓	Fasse zusammen.
$\displaystyle \left(\begin{pmatrix}4\\2\\4\end{pmatrix}+t\cdot\begin{pmatrix} 1 \\y \\ 4 \end{pmatrix}\right)^2$	$=$	$\displaystyle 10$
	↓	Vereinfache weiter.
$\displaystyle \begin{pmatrix}4+t\\2+yt\\4+4t\end{pmatrix}^2$	$=$	$\displaystyle 10$
	↓	Rechne das Skalarprodukt aus.
$\displaystyle (4+t)^2+(2+yt)^2+(4+4t)^2$	$=$	$\displaystyle 10$
	↓	Löse die Klammern auf und vergiss dabei nicht die binomische Formel anzuwenden.
$\displaystyle 16+8t+t^2+4+4yt+(yt)^2+16+32t+16t^2$	$=$	$\displaystyle 10$
	↓	Fasse die linke Seite zusammen.
$\displaystyle 17t^2+y^2t^2+40t+4yt+36$	$=$	$\displaystyle 10$	$\displaystyle -10$
	↓	Klammere aus.
$\displaystyle (17+y^2)\cdot t^2+(40+4y)\cdot t+26$	$=$	$\displaystyle 0$

Du hast die quadratische Gleichung $(17+y^2)\cdot t^2+(40+4y)\cdot t+26=0$ mit der Unbekannten $t$ erhalten. Diese Gleichung kannst du mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel lösen. Hier erfolgt die Lösung mit der Mitternachtsformel. Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein:

$a = 17 + y^{2}$ , $b = 40 + 4 y$ , $c = 26$

$\displaystyle t_{1{,}2}$	$=$	$\displaystyle \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
	↓	Setze die Werte $a = 17 + y^{2}$ , $b = 40 + 4 y$ und $c = 26$ ein.
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle \dfrac{-(40+4y)\pm\sqrt{(40+4y)^2-4\cdot(17+y^2)\cdot26}}{2\cdot(17+y^2)}$

Wenn die Gerade $g$ eine Tangente sein soll, dann darf es nur eine Lösung für die quadratische Gleichung geben. Die Diskriminante muss gleich Null sein. $D=(40+4y)^2-4\cdot (17+y^2)\cdot 26=0$

$\displaystyle (40+4y)^2-4\cdot (17+y^2)\cdot 26$	$=$	$\displaystyle 0$
	↓	Vereinfache die linke Seite. Vergiss nicht die binomische Formel anzuwenden.
$\displaystyle 1600+320y+16y^2-1768-104y^2$	$=$	$\displaystyle 0$
	↓	Vereinfache.
$\displaystyle -88y^2+320y-168$	$=$	$\displaystyle 0$	$\displaystyle \cdot (-1)$
$\displaystyle 88y^2 −320y+168$	$=$	$\displaystyle 0$

Du hast die quadratische Gleichung $88 y^{2} - 320 y + 168 = 0$ mit der Unbekannten $y$ erhalten. Die Gleichung kannst du mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel lösen. Hier erfolgt die Lösung mit der Mitternachtsformel. Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein: $a = 88$ , $b = - 320$ , $c = 168$

$\displaystyle y_{1{,}2}$	$=$	$\displaystyle \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
	↓	Setze $a = 88$ , $b = - 320$ , $c = 168$ ein.
	$=$	$\displaystyle \dfrac{-(-320)\pm\sqrt{320^2-4\cdot 88\cdot 168}}{2\cdot 88}$
	↓	Vereinfache.
	$=$	$\displaystyle \dfrac{320\pm\sqrt{102400-59136}}{176}$
	↓	Vereinfache.
	$=$	$\displaystyle \dfrac{320\pm208}{176}$

Fall: $+$

$y_1=\dfrac{528}{176}=3$

Fall: $-$

$y_2=\dfrac{112}{176}=\dfrac{7}{11}$

Antwort: Die quadratische Gleichung hat die Lösungsmenge: $\;\mathbb{L}=\{\dfrac{7}{11};3\}$

Da es für $y$ zwei Lösungen gibt, erhältst du auch zwei Tangentengleichungen.

Setze in $g:\;\vec X=\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\y \\ 4\end{pmatrix}$ für $y$ nacheinander die beiden Werte $y_{1} = 3$ und $y_2=\dfrac{7}{11}$ ein.

$g_{Tangente_1}:\;\vec X=\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\3 \\ 4\end{pmatrix} $ und

$g_{Tangente_2}:\;\vec X=\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\\dfrac{7}{11} \\ 4\end{pmatrix}$

Berührpunkte berechnen

Da die Diskriminante den Wert Null hat, gibt es nur eine Lösung bei der Schnittpunktsberechnung zwischen Gerade $g$ und Kugel $K$ .

$\displaystyle t_{1{,}2}$	$=$	$\displaystyle \dfrac{-(40+4y)\pm\sqrt{(40+4y)^2-4\cdot(17+y^2)\cdot26}}{2\cdot(17+y^2)}$
	↓	Der Term unter der Wurzel ist die Diskriminante $D$ .
	$=$	$\displaystyle \dfrac{-(40+4y)\pm\sqrt{D}}{2\cdot(17+y^2)}$
	↓	Setze $D = 0$ , da es nur eine Lösung geben soll.
$\displaystyle t$	$=$	$\displaystyle -\dfrac{40+4y}{2\cdot(17+y^2)}$
	↓	Klammere im Zähler $2$ aus.
	$=$	$\displaystyle -\dfrac{2\cdot (20+2y)}{2\cdot(17+y^2)}$
	↓	Kürze.
	$=$	$\displaystyle -\dfrac{20+2y}{17+y^2}$

Du hast für $t$ einen Term erhalten, der die y-Koordinate des Richtungsvektors der Geraden $g$ enthält. Für die beiden berechneten y-Werte $y_{1} = 3$ und $y_2 =\dfrac{7}{11}$ erhältst du zwei Berührpunkte.

Für $y_{1} = 3$ folgt $t_1=-\dfrac{20+2\cdot 3}{17+3^2}=-\dfrac{26}{26}=-1$

Setze $t_{1} = - 1$ in $g_{Tangente_1}:\;\vec X=\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\3 \\ 4\end{pmatrix}$ ein:

$\vec X_{B_1}=\begin{pmatrix}5\\4\\7\end{pmatrix}-1\cdot\begin{pmatrix}1 \\3 \\ 4\end{pmatrix}=\begin{pmatrix}4\\1\\3\end{pmatrix}\;\;\Rightarrow\;\;B_1(4|1|3)$

Für $y_2 =\dfrac{7}{11}$ folgt $t_2=-\dfrac{20+2\cdot \dfrac{7}{11}}{17+\left(\dfrac{7}{11}\right)^2}=-\dfrac{20+\dfrac{14}{11}}{17+\dfrac{49}{121}}=-\dfrac{\dfrac{234}{11}}{\dfrac{2106}{121}}=-\dfrac{11}{9}$

Setze $t_2=-\dfrac{11}{9}$ in $g_{Tangente_2}:\;\vec X=\begin{pmatrix}5\\4\\7\end{pmatrix}+t\cdot\begin{pmatrix}1 \\\dfrac{7}{11} \\ 4\end{pmatrix}$ ein:

$\vec X_{B_2}=\begin{pmatrix}5\\4\\7\end{pmatrix}-\dfrac{11}{9}\cdot\begin{pmatrix}1 \\\dfrac{7}{11} \\ 4\end{pmatrix}=\begin{pmatrix}5-\dfrac{11}{9}\\4-\dfrac{7}{9}\\7-\dfrac{44}{9}\end{pmatrix}=\begin{pmatrix}\dfrac{34}{9}\\\dfrac{29}{9}\\\dfrac{19}{9}\end{pmatrix}\;\;\Rightarrow\;\;B_2\left(\dfrac{34}{9}|\dfrac{29}{9}|\dfrac{19}{9}\right)$

Antwort: Die beiden Berührpunkte haben die Koordinaten $B_{1} (4 ∣ 1 ∣ 3)$ und $B_2\left(\dfrac{34}{9}|\dfrac{29}{9}|\dfrac{19}{9}\right)$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Wähle für die Koordinate $y$ in der oben angegebenen Geraden $g$ die Werte $y_{a} = 0$ und $y_{b} = 2$ .

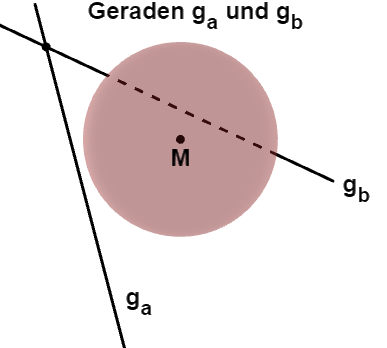
Welche Lage haben die beiden Geraden $g_{a}$ und $g_{b}$ bezüglich der Kugel $K$ ?

$\displaystyle D$	$=$	$\displaystyle (40+4y)^2-4\cdot (17+y^2)\cdot 26$
	↓	Setze für $y$ den Wert $0$ ein.
	$=$	$\displaystyle (40+4\cdot 0)^2-4\cdot (17+0^2)\cdot 26$
	↓	Vereinfache.
	$=$	$\displaystyle 1600-1768$
	$=$	$\displaystyle -168$

$\displaystyle D$	$=$	$\displaystyle (40+4y)^2-4\cdot (17+y^2)\cdot 26$
	↓	Setze für $y$ den Wert $2$ ein.
	$=$	$\displaystyle (40+4\cdot 2)^2-4\cdot (17+2^2)\cdot 26$
	↓	Vereinfache.
	$=$	$\displaystyle 48^2-4\cdot21\cdot 26$
	$=$	$\displaystyle 2304-2184$
	$=$	$\displaystyle 120$