Aufgaben zu Kugeln und Geraden

Hier findest du Übungsaufgaben zu Kugeln und Geraden. Lerne, die verschiedenen Lagebeziehungen zwischen Kugeln und Geraden zu untersuchen!

1
Gegeben sind die Kugel $K$ mit dem Mittelpunkt $M$ und dem Radius $r$ und eine Gerade. Untersuche die gegenseitige Lage der Geraden bezüglich der Kugel. Gib gegebenenfalls alle Schnittpunkte an.
1. Mittelpunkt der Kugel $M (5 | 2 | 1)$ , Kugelradius $r = 7$
  Gerade $g : \vec{X} = (\begin{array}{c} - 1 \\ 4 \\ 1 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugelgleichung
  Aufstellen der Kugelgleichung
  $M (5 | 2 | 1)$ , $r = 7$
  $K : (\vec{x} - \vec{m})^{2} = r^{2}$
  $K : {(\vec{x} - (\begin{array}{c} 5 \\ 2 \\ 1 \end{array}))}^{2} = 7^{2} = 49$
  Gerade g in $K$ einsetzen
  ${((\begin{array}{c} - 1 \\ 4 \\ 1 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}) - (\begin{array}{c} 5 \\ 2 \\ 1 \end{array}))}^{2} = 49$
  Fasse zusammen.
  ${((\begin{array}{c} - 6 \\ 2 \\ 0 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}))}^{2} = 49$
  Vereinfache weiter.
  ${(\begin{array}{c} - 6 + t \\ 2 + 0 \\ 0 + 2 t \end{array})}^{2} = 49$
  Rechne das Skalarprodukt aus.
  $(- 6 + t)^{2} + 2^{2} + (2 t)^{2} = 49$
  Vergiss nicht die binomische Formel anzuwenden!
  $36 - 12 t + t^{2} + 4 + 4 t^{2}$ $=$ $49$
  $40 - 12 t + 5 t^{2}$ $=$ $49$ $- 49$
  ↓
  linke Seite sortieren
  $5 t^{2} - 12 t - 9$ $=$ $0$
  Du hast eine quadratische Gleichung erhalten. Diese kannst du nun mit der Mitternachtsformel (abc-Formel) oder p-q-Formel lösen. Hier erfolgt die Lösung mit der Mitternachtsformel.
  Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein: $a = 5$ , $b = - 12$ , $c = - 9$
  $t_{1,2}$ $=$ $\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
  ↓
  Setze $a = 5$ , $b = - 12$ , $c = - 9$ ein
  $=$ $\frac{- (- 12) \pm \sqrt{(- 12)^{2} - 4 \cdot 5 \cdot (- 9)}}{2 \cdot 5}$
  ↓
  vereinfache
  $=$ $\frac{12 \pm \sqrt{144 + 180}}{10}$
  $=$ $\frac{12 \pm \sqrt{324}}{10}$
  $=$ $\frac{12 \pm 18}{10}$
  $t_{1}$ $=$ $3$
  $t_{2}$ $=$ $- 0,6$
  Die quadratische Gleichung hat somit die Lösungsmenge $𝕃 = {- 0,6; 3}$ . Da es zwei Lösungen gibt, schneidet die Gerade $g$ die Kugel $K$ in zwei Punkten. Die Gerade g ist also eine Sekante.
  Schnittpunkte berechnen
  Setze die zwei gefundenen Parameter $t_{1}$ und $t_{2}$ in die Geradengleichung ein.
  $t_{1} = 3$ :
  ${\vec{X}}_{S_{1}} = (\begin{array}{c} - 1 \\ 4 \\ 1 \end{array}) + 3 \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}) = (\begin{array}{c} - 1 + 3 \\ 4 + 0 \\ 1 + 6 \end{array}) = (\begin{array}{c} 2 \\ 4 \\ 7 \end{array})$
  $t_{2} = - 0,6$ :
  ${\vec{X}}_{S_{2}} = (\begin{array}{c} - 1 \\ 4 \\ 1 \end{array}) + (- 0,6) \cdot (\begin{array}{c} 1 \\ 0 \\ 2 \end{array}) = (\begin{array}{c} - 1 - 0,6 \\ 4 + 0 \\ 1 - 1,2 \end{array}) = (\begin{array}{c} - 1,6 \\ 4 \\ - 0,2 \end{array})$
  Antwort: Die beiden Schnittpunkte haben die Koordinaten $S_{1} (2 | 4 | 7)$ und $S_{2} (- 1,6 | 4 | - 0,2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Stelle die Kugelgleichung $K$ in vektorieller Form auf und setze die Geradengleichung $g$ in die Gleichung $K$ ein. Ergeben sich bei der Lösung der Gleichung zwei Lösungen, dann ist die Gerade eine Sekante. Hat die Gleichung genau eine Lösung, dann ist die Gerade eine Tangente. Findest du hingegen keine Lösung der Gleichung, dann ist die Gerade eine Passante.
2. Mittelpunkt der Kugel $M (1 | 2 | 4)$ , Kugelradius $r = \sqrt{21}$
  Gerade $g : \vec{X} = (\begin{array}{c} 1 \\ - 2 \\ 9 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 0 \\ - 2 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugelgleichung
  Aufstellen der Kugelgleichung
  $M (1 | 2 | 4)$ , $r = \sqrt{21}$
  $K : (\vec{x} - \vec{m})^{2} = r^{2}$
  $K : {(\vec{x} - (\begin{array}{c} 1 \\ 2 \\ 4 \end{array}))}^{2} = {(\sqrt{21})}^{2} = 21$
  Gerade g in $K$ einsetzen
  ${((\begin{array}{c} 1 \\ - 2 \\ 9 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 0 \\ - 2 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 4 \end{array}))}^{2} = 21$
  Fasse zusammen.
  ${((\begin{array}{c} 0 \\ - 4 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 0 \\ - 2 \end{array}))}^{2} = 21$
  Vereinfache weiter.
  ${(\begin{array}{c} 0 + t \\ - 4 + 0 \\ 5 - 2 t \end{array})}^{2} = 21$
  Rechne das Skalarprodukt aus.
  $t^{2} + (- 4)^{2} + (5 - 2 t)^{2} = 21$
  Vergiss nicht die binomische Formel anzuwenden!
  $t^{2} + 16 + 25 - 20 t + 4 t^{2}$ $=$ $21$
  ↓
  fasse zusammen
  $5 t^{2} - 20 t + 41$ $=$ $21$ $- 21$
  $5 t^{2} - 20 t + 20$ $=$ $0$ $: 5$
  $t^{2} - 4 t + 4$ $=$ $0$
  ↓
  wende eine binomische Formel an
  ${(t - 2)}^{2}$ $=$ $0$
  Die Lösung dieser quadratischen Gleichung kann direkt abgelesen werden: $t = 2$
  Die quadratische Gleichung hat die Lösungsmenge $𝕃 = {2}$ . Da es genau eine Lösung gibt, haben die Gerade $g$ und die Kugel $K$ einen Punkt gemeinsam, d.h. die Gerade $g$ ist eine Tangente an die Kugel $K$ .
  Schnittpunktberechnung
  Da es nur einen gemeinsamen Punkt zwischen der Kugel und der Geraden gibt, ist dieser Punkt ein Berührpunkt.
  Setze den Wert $t = 2$ in die Geradengleichung ein.
  ${\vec{X}}_{B} = (\begin{array}{c} 1 \\ - 2 \\ 9 \end{array}) + 2 \cdot (\begin{array}{c} 1 \\ 0 \\ - 2 \end{array}) = (\begin{array}{c} 1 + 2 \\ - 2 + 0 \\ 9 - 4 \end{array}) = (\begin{array}{c} 3 \\ - 2 \\ 5 \end{array})$
  Antwort: Der Berührpunkt hat die Koordinaten $B (3 | - 2 | 5) .$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Stelle die Kugelgleichung $K$ in vektorieller Form auf und setze die Geradengleichung $g$ in die Gleichung $K$ ein. Ergeben sich bei der Lösung der Gleichung zwei Lösungen, dann ist die Gerade eine Sekante. Hat die Gleichung genau eine Lösung, dann ist die Gerade eine Tangente. Findest du hingegen keine Lösung der Gleichung, dann ist die Gerade eine Passante.
3. Mittelpunkt der Kugel $M (1 | 7 | 0)$ , Kugelradius $r = 6$
  Gerade $g : \vec{X} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 0 \\ 1 \\ 4 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugelgleichung
  Aufstellen der Kugelgleichung
  $M (1 | 7 | 0)$ , $r = 6$
  $K : (\vec{x} - \vec{m})^{2} = r^{2}$
  $K : {(\vec{x} - (\begin{array}{c} 1 \\ 7 \\ 0 \end{array}))}^{2} = 6^{2} = 36$
  Gerade g in $K$ einsetzen
  ${((\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 0 \\ 1 \\ 4 \end{array}) - (\begin{array}{c} 1 \\ 7 \\ 0 \end{array}))}^{2} = 36$
  Fasse zusammen.
  ${((\begin{array}{c} 0 \\ - 5 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 0 \\ 1 \\ 4 \end{array}))}^{2} = 36$
  Vereinfache weiter.
  $0^{2} + (- 5 + t)^{2} + (5 + 4 t)^{2} = 36$
  Vergiss nicht die binomische Formel anzuwenden!
  $25 - 10 t + t^{2} + 25 + 40 t + 16 t^{2}$ $=$ $36$
  ↓
  fasse zusammen
  $17 t^{2} + 30 t + 50$ $=$ $36$ $- 36$
  $17 t^{2} + 30 t + 14$ $=$ $0$
  Die quadratische Gleichung löst du nun mit der Mitternachtsformel (abc-Formel) oder p-q-Formel.
  Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein: $a = 17$ , $b = 30$ , $c = 14$
  $t_{1,2}$ $=$ $\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
  ↓
  Setze $a = 17$ , $b = 30$ , $c = 14$ ein
  $=$ $\frac{- 30 \pm \sqrt{30^{2} - 4 \cdot 17 \cdot 14}}{2 \cdot 17}$
  ↓
  vereinfache
  $=$ $\frac{- 30 \pm \sqrt{900 - 952}}{34}$
  $=$ $\frac{- 30 \pm \sqrt{- 52}}{34}$
  Du hast bei der Lösung der Gleichung eine negative Wurzel erhalten, d.h. die Gleichung hat keine reelle Lösung: $𝕃 = {}$
  Die Gerade $g$ hat mit der Kugel $K$ keine gemeinsamen Punkte, d.h. die Gerade $g$ ist eine Passante.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Stelle die Kugelgleichung $K$ in vektorieller Form auf und setze die Geradengleichung $g$ in die Gleichung $K$ ein. Ergeben sich bei der Lösung der Gleichung zwei Lösungen, dann ist die Gerade eine Sekante. Hat die Gleichung genau eine Lösung, dann ist die Gerade eine Tangente. Findest du hingegen keine Lösung der Gleichung, dann ist die Gerade eine Passante.

Gegeben sind eine Kugel $K$ mit Mittelpunkt $M (3 | - 1 | 2)$ , Radius $r = \sqrt{11}$ und eine Gerade

$g : \vec{X} = (\begin{array}{c} 2 \\ 0 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 2 \\ - 4 \\ - 4 \end{array})$ .

Zeige, dass die Gerade eine Sekante der Kugel ist. Gib auch beide Schnittpunkte an.

Gib für die beiden Schnittpunkte $S_{1}$ und $S_{2}$ jeweils die zugehörende Tangentialebene in Koordinatenform an.

Zeige, dass sich die beiden Tangentialebenen $E_{T_{1}}$ und $E_{T_{2}}$ schneiden und berechne die Gleichung der Schnittgeraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lage zweier Ebenen
Schnitt von $E_{T_{1}}$ und $E_{T_{2}}$
Die beiden Tangentialebenen $E_{T_{1}}$ und $E_{T_{2}}$ haben die beiden Normalenvektoren:
${\vec{n}}_{T_{1}} = (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$ und ${\vec{n}}_{T_{2}} = (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$ .
Die Normalenvektoren sind nicht Vielfache voneinander. Die beiden Ebenen sind somit nicht parallel, d.h. sie schneiden sich.
Berechnung der Schnittgeraden
Die beiden Ebenengleichungen liegen in der Koordinatenform vor. Die Berechnung der Schnittgeraden erfolgt durch Lösen eines Gleichungssystems aus $2$ Gleichungen mit $3$ Unbekannten. Dabei gibt es mehrere Lösungswege z.B. das Einsetzungsverfahren oder das Additionsverfahren. Die Lösung des Gleichungssystems erfolgt hier mit dem Additionsverfahren.
Die Tangentialebene $E_{T_{1}}$ ist Gleichung $(I)$ und die Tangentialebene $E_{T_{2}}$ ist Gleichung $(I I)$ .
Eliminiere eine Variable z.B. die Variable $x_{1}$ .
Rechne $(I) + (I I)$ :
$\begin{array}{l} \begin{array}{cccccccl} (I) : - x_{1} & + & x_{2} & + & 3 x_{3} & = & 13 \\ + (I I) : x_{1} & - & 3 x_{2} & - & x_{3} & = & 15 \end{array} \\ 0 x_{1} - 2 x_{2} + 2 x_{3} = 28 \Rightarrow (I I I) : x_{2} = - 14 + x_{3} \end{array}$
Du hast die Gleichung $(I I I) : x_{2} = - 14 + x_{3}$ erhalten.
Bei $2$ Gleichungen mit $3$ Unbekannten ist eine Unbekannte frei wählbar. Wähle z.B. $x_{3} = s$ .
Somit lautet die Gleichung $(I I I^{'}) : x_{2} = - 14 + s$ .
Setze die Gleichung $(I I I^{'})$ und $x_{3} = s$ in Gleichung $(I I)$ ein.
$(I I) : x_{1} - 3 x_{2} - x_{3}$ $=$ $15$
↓
Setze $x_{2} = - 14 + s$ und $x_{3} = s$ ein.
$x_{1} - 3 \cdot (- 14 + s) - s$ $=$ $15$
↓
Löse die Klammer auf.
$x_{1} + 42 - 3 s - s$ $=$ $15$
↓
Vereinfache.
$x_{1} + 42 - 4 s$ $=$ $15$ $- 42 + 4 s$
$x_{1}$ $=$ $- 27 + 4 s$
Schreibe die drei erhaltenen Gleichungen für $x_{1}$ , $x_{2}$ und $x_{3}$ untereinander und sortiere entsprechend.
$g_{S c h n i t t} : \vec{X} = (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{c} - 27 + 4 s \\ - 14 + s \\ 0 + s \end{array}) = (\begin{array}{c} - 27 \\ - 14 \\ 0 \end{array}) + s (\begin{array}{c} 4 \\ 1 \\ 1 \end{array})$
Antwort: Die Gleichung der Schnittgeraden der beiden Tangentialebenen lautet:
$g_{S c h n i t t} : \vec{X} = (\begin{array}{c} - 27 \\ - 14 \\ 0 \end{array}) + s (\begin{array}{c} 4 \\ 1 \\ 1 \end{array})$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Unter welchen Winkel schneiden sich die beiden Tangentialebenen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zweier Ebenen
Für den Schnittwinkel $α$ zwischen zwei Ebenen gilt folgende Formel:
$\cos α = \frac{| {\vec{n}}_{1} \circ {\vec{n}}_{2} |}{| {\vec{n}}_{1} | \cdot | {\vec{n}}_{2} |}$
Im Zähler des Bruches steht der Betrag des Skalarproduktes der beiden Normalenvektoren ${\vec{n}}_{1}$ und ${\vec{n}}_{2}$ der beiden Tangentialebenen $E_{T_{1}} : - x_{1} + x_{2} + 3 x_{3} = 13$ und $E_{T_{2}} : x_{1} - 3 x_{2} - x_{3} = 15$ . Im Nenner des Bruches steht das Produkt der Beträge der beiden Normalenvektoren.
Lies die Normalenvektoren aus den Koordinatengleichungen ab:
${\vec{n}}_{1} = (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$ und ${\vec{n}}_{2} = (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$
Für den Betrag von ${\vec{n}}_{1}$ gilt: $| {\vec{n}}_{1} | = \sqrt{(- 1)^{2} + 1^{2} + 3^{2}} = \sqrt{1 + 1 + 9} = \sqrt{11}$
Für den Betrag von ${\vec{n}}_{2}$ gilt: $| {\vec{n}}_{2} | = \sqrt{1^{2} + (- 3)^{2} + (- 1)^{2}} = \sqrt{1 + 9 + 1} = \sqrt{11}$
Setze in die oben genannte Formel ein:
$\cos α$ $=$ $\frac{| (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array}) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array}) |}{\sqrt{11} \cdot \sqrt{11}}$
↓
Berechne das Skalarprodukt und vereinfache.
$=$ $\frac{| - 1 - 3 - 3 |}{11}$
↓
Vereinfache.
$=$ $\frac{| - 7 |}{11}$
↓
Berechne den Betrag.
$=$ $\frac{7}{11}$
Du hast die Gleichung $\cos α = \frac{7}{11}$ erhalten. Durch Anwendung der Umkehrfunktion des Kosinus kannst du den Winkel $α$ berechnen.
Hinweis: Benutze auf dem Taschenrechner die Funktion $\cos^{- 1} (x)$ .
$α = \arccos (\frac{7}{11}) \approx {50,48}^{\circ}$
Antwort: Der Schnittwinkel zwischen den beiden Tangentialebenen beträgt rund ${50,5}^{\circ}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Lies die Normalenvektoren aus den Koordinatengleichungen ab und setze sie in die Formel für den Schnittwinkel zweier Ebenen ein.

Gegeben sind eine Kugel $K$ mit Mittelpunkt $M (1 | 2 | 3)$ , Radius $r = \sqrt{10}$ und eine Gerade $g : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ y \\ 4 \end{array})$ .

Für welchen Wert von $y$ ist die Gerade $g$ eine Tangente an die Kugel $K$ ? Gib auch den Berührpunkt an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel und Geraden

Aufstellen der Kugelgleichung

$M (1 | 2 | 3)$ , $r = \sqrt{10}$

$K : (\vec{x} - \vec{m})^{2} = r^{2}$

$K : {(\vec{x} - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}))}^{2} = {(\sqrt{10})}^{2} = 10$

Setze die Gleichung der Geraden für den Vektor $\vec{x}$ in die Kugelgleichung ein.

$g : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ y \\ 4 \end{array})$ in $K : {(\vec{x} - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}))}^{2} = 10$ einsetzen:

${((\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ y \\ 4 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}))}^{2}$	$=$	$10$
	↓	Fasse zusammen.
${((\begin{array}{c} 4 \\ 2 \\ 4 \end{array}) + t \cdot (\begin{array}{c} 1 \\ y \\ 4 \end{array}))}^{2}$	$=$	$10$
	↓	Vereinfache weiter.
${(\begin{array}{c} 4 + t \\ 2 + y t \\ 4 + 4 t \end{array})}^{2}$	$=$	$10$
	↓	Rechne das Skalarprodukt aus.
$(4 + t)^{2} + (2 + y t)^{2} + (4 + 4 t)^{2}$	$=$	$10$
	↓	Löse die Klammern auf und vergiss dabei nicht die binomische Formel anzuwenden.
$16 + 8 t + t^{2} + 4 + 4 y t + (y t)^{2} + 16 + 32 t + 16 t^{2}$	$=$	$10$
	↓	Fasse die linke Seite zusammen.
$17 t^{2} + y^{2} t^{2} + 40 t + 4 y t + 36$	$=$	$10$	$- 10$
	↓	Klammere aus.
$(17 + y^{2}) \cdot t^{2} + (40 + 4 y) \cdot t + 26$	$=$	$0$

Du hast die quadratische Gleichung $(17 + y^{2}) \cdot t^{2} + (40 + 4 y) \cdot t + 26 = 0$ mit der Unbekannten $t$ erhalten. Diese Gleichung kannst du mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel lösen. Hier erfolgt die Lösung mit der Mitternachtsformel. Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein:

$a = 17 + y^{2}$ , $b = 40 + 4 y$ , $c = 26$

$t_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze die Werte $a = 17 + y^{2}$ , $b = 40 + 4 y$ und $c = 26$ ein.
$x_{1,2}$	$=$	$\frac{- (40 + 4 y) \pm \sqrt{(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26}}{2 \cdot (17 + y^{2})}$

Wenn die Gerade $g$ eine Tangente sein soll, dann darf es nur eine Lösung für die quadratische Gleichung geben. Die Diskriminante muss gleich Null sein. $D = (40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26 = 0$

$(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26$	$=$	$0$
	↓	Vereinfache die linke Seite. Vergiss nicht die binomische Formel anzuwenden.
$1600 + 320 y + 16 y^{2} - 1768 - 104 y^{2}$	$=$	$0$
	↓	Vereinfache.
$- 88 y^{2} + 320 y - 168$	$=$	$0$	$\cdot (- 1)$
$88 y^{2} - 320 y + 168$	$=$	$0$

Du hast die quadratische Gleichung $88 y^{2} - 320 y + 168 = 0$ mit der Unbekannten $y$ erhalten. Die Gleichung kannst du mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel lösen. Hier erfolgt die Lösung mit der Mitternachtsformel. Lies dazu die Werte für $a$ , $b$ und $c$ ab und setze sie in die Mitternachtsformel ein: $a = 88$ , $b = - 320$ , $c = 168$

$y_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = 88$ , $b = - 320$ , $c = 168$ ein.
	$=$	$\frac{- (- 320) \pm \sqrt{320^{2} - 4 \cdot 88 \cdot 168}}{2 \cdot 88}$
	↓	Vereinfache.
	$=$	$\frac{320 \pm \sqrt{102400 - 59136}}{176}$
	↓	Vereinfache.
	$=$	$\frac{320 \pm 208}{176}$

Fall: $+$

$y_{1} = \frac{528}{176} = 3$

Fall: $-$

$y_{2} = \frac{112}{176} = \frac{7}{11}$

Antwort: Die quadratische Gleichung hat die Lösungsmenge: $𝕃 = {\frac{7}{11}; 3}$

Da es für $y$ zwei Lösungen gibt, erhältst du auch zwei Tangentengleichungen.

Setze in $g : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ y \\ 4 \end{array})$ für $y$ nacheinander die beiden Werte $y_{1} = 3$ und $y_{2} = \frac{7}{11}$ ein.

$g_{T a n g e n t e_{1}} : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 3 \\ 4 \end{array}) $ und

$g_{T a n g e n t e_{2}} : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ \frac{7}{11} \\ 4 \end{array})$

Berührpunkte berechnen

Da die Diskriminante den Wert Null hat, gibt es nur eine Lösung bei der Schnittpunktsberechnung zwischen Gerade $g$ und Kugel $K$ .

$t_{1,2}$	$=$	$\frac{- (40 + 4 y) \pm \sqrt{(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26}}{2 \cdot (17 + y^{2})}$
	↓	Der Term unter der Wurzel ist die Diskriminante $D$ .
	$=$	$\frac{- (40 + 4 y) \pm \sqrt{D}}{2 \cdot (17 + y^{2})}$
	↓	Setze $D = 0$ , da es nur eine Lösung geben soll.
$t$	$=$	$- \frac{40 + 4 y}{2 \cdot (17 + y^{2})}$
	↓	Klammere im Zähler $2$ aus.
	$=$	$- \frac{2 \cdot (20 + 2 y)}{2 \cdot (17 + y^{2})}$
	↓	Kürze.
	$=$	$- \frac{20 + 2 y}{17 + y^{2}}$

Du hast für $t$ einen Term erhalten, der die y-Koordinate des Richtungsvektors der Geraden $g$ enthält. Für die beiden berechneten y-Werte $y_{1} = 3$ und $y_{2} = \frac{7}{11}$ erhältst du zwei Berührpunkte.

Für $y_{1} = 3$ folgt $t_{1} = - \frac{20 + 2 \cdot 3}{17 + 3^{2}} = - \frac{26}{26} = - 1$

Setze $t_{1} = - 1$ in $g_{T a n g e n t e_{1}} : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ 3 \\ 4 \end{array})$ ein:

${\vec{X}}_{B_{1}} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) - 1 \cdot (\begin{array}{c} 1 \\ 3 \\ 4 \end{array}) = (\begin{array}{c} 4 \\ 1 \\ 3 \end{array}) \Rightarrow B_{1} (4 | 1 | 3)$

Für $y_{2} = \frac{7}{11}$ folgt $t_{2} = - \frac{20 + 2 \cdot \frac{7}{11}}{17 + {(\frac{7}{11})}^{2}} = - \frac{20 + \frac{14}{11}}{17 + \frac{49}{121}} = - \frac{\frac{234}{11}}{\frac{2106}{121}} = - \frac{11}{9}$

Setze $t_{2} = - \frac{11}{9}$ in $g_{T a n g e n t e_{2}} : \vec{X} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 1 \\ \frac{7}{11} \\ 4 \end{array})$ ein:

${\vec{X}}_{B_{2}} = (\begin{array}{c} 5 \\ 4 \\ 7 \end{array}) - \frac{11}{9} \cdot (\begin{array}{c} 1 \\ \frac{7}{11} \\ 4 \end{array}) = (\begin{array}{c} 5 - \frac{11}{9} \\ 4 - \frac{7}{9} \\ 7 - \frac{44}{9} \end{array}) = (\begin{array}{c} \frac{34}{9} \\ \frac{29}{9} \\ \frac{19}{9} \end{array}) \Rightarrow B_{2} (\frac{34}{9} | \frac{29}{9} | \frac{19}{9})$

Antwort: Die beiden Berührpunkte haben die Koordinaten $B_{1} (4 | 1 | 3)$ und $B_{2} (\frac{34}{9} | \frac{29}{9} | \frac{19}{9})$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Wähle für die Koordinate $y$ in der oben angegebenen Geraden $g$ die Werte $y_{a} = 0$ und $y_{b} = 2$ .
Welche Lage haben die beiden Geraden $g_{a}$ und $g_{b}$ bezüglich der Kugel $K$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel und Geraden
Die oben berechnete Diskriminante lautet : $D = (40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26$
Setze nacheinander die gegebenen Werte für y ein.
$y_{a} = 0$
$D$ $=$ $(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26$
↓
Setze für $y$ den Wert $0$ ein.
$=$ $(40 + 4 \cdot 0)^{2} - 4 \cdot (17 + 0^{2}) \cdot 26$
↓
Vereinfache.
$=$ $1600 - 1768$
$=$ $- 168$
Antwort: Die Diskriminante $D$ ist negativ, d.h. die quadratische Gleichung hat keine Lösung. Die Gerade $g_{a}$ schneidet die Kugel $K$ nicht. Die Gerade ist eine Passante.
$y_{b} = 2$
$D$ $=$ $(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26$
↓
Setze für $y$ den Wert $2$ ein.
$=$ $(40 + 4 \cdot 2)^{2} - 4 \cdot (17 + 2^{2}) \cdot 26$
↓
Vereinfache.
$=$ $48^{2} - 4 \cdot 21 \cdot 26$
$=$ $2304 - 2184$
$=$ $120$
Antwort: Die Diskriminante ist positiv, d.h. die quadratische Gleichung hat zwei Lösungen. Die Gerade $g_{b}$ schneidet die Kugel $K$ in zwei Punkten. Die Gerade ist eine Sekante.
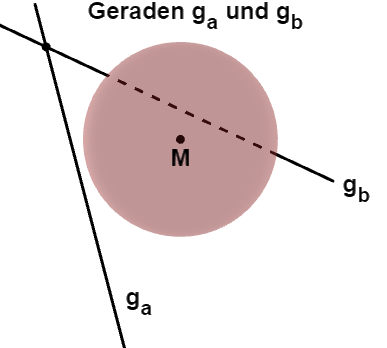
Die nebenstehende Abbildung ist nicht verlangt worden.

Sie dient nur der Veranschaulichung.
$g_{a}$ ist eine Passante
$g_{b}$ ist eine Sekante
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
In Aufgabe a) hast du bereits die Gerade $g$ mit der Kugel $K$ geschnitten. Die Lösung der quadratischen Gleichung enthält die unbekannte Koordinate $y$ . Der Wert der Diskriminanten $D$ entscheidet über die Lage der Geraden gegenüber der Kugel. Berechne die Diskriminante $D$ mit den beiden y-Werten und entscheide dann über die Lage der beiden Geraden $g_{a}$ und $g_{b}$ bezüglich der Kugel $K$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zu Kugeln und Geraden

Aufstellen der Kugelgleichung

Gerade g in $K$ einsetzen

Schnittpunkte berechnen

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Gerade g in $K$ einsetzen

Schnittpunktberechnung

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Gerade g in $K$ einsetzen

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Schnittpunkte berechnen

Hast du eine Frage oder Feedback?

Aufstellen der Tangentialebenengleichung im Punkt $S_{1}$

Aufstellen der Tangentialebenengleichung im Punkt $S_{2}$

Hast du eine Frage oder Feedback?

Schnitt von $E_{T_{1}}$ und $E_{T_{2}}$

Berechnung der Schnittgeraden

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Berührpunkte berechnen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$36 - 12 t + t^{2} + 4 + 4 t^{2}$	$=$	$49$
$40 - 12 t + 5 t^{2}$	$=$	$49$	$- 49$
	↓	linke Seite sortieren
$5 t^{2} - 12 t - 9$	$=$	$0$

$t_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = 5$ , $b = - 12$ , $c = - 9$ ein
	$=$	$\frac{- (- 12) \pm \sqrt{(- 12)^{2} - 4 \cdot 5 \cdot (- 9)}}{2 \cdot 5}$
	↓	vereinfache
	$=$	$\frac{12 \pm \sqrt{144 + 180}}{10}$
	$=$	$\frac{12 \pm \sqrt{324}}{10}$
	$=$	$\frac{12 \pm 18}{10}$
$t_{1}$	$=$	$3$
$t_{2}$	$=$	$- 0,6$

$t^{2} + 16 + 25 - 20 t + 4 t^{2}$	$=$	$21$
	↓	fasse zusammen
$5 t^{2} - 20 t + 41$	$=$	$21$	$- 21$
$5 t^{2} - 20 t + 20$	$=$	$0$	$: 5$
$t^{2} - 4 t + 4$	$=$	$0$
	↓	wende eine binomische Formel an
${(t - 2)}^{2}$	$=$	$0$

$25 - 10 t + t^{2} + 25 + 40 t + 16 t^{2}$	$=$	$36$
	↓	fasse zusammen
$17 t^{2} + 30 t + 50$	$=$	$36$	$- 36$
$17 t^{2} + 30 t + 14$	$=$	$0$

$t_{1,2}$	$=$	$\frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
	↓	Setze $a = 17$ , $b = 30$ , $c = 14$ ein
	$=$	$\frac{- 30 \pm \sqrt{30^{2} - 4 \cdot 17 \cdot 14}}{2 \cdot 17}$
	↓	vereinfache
	$=$	$\frac{- 30 \pm \sqrt{900 - 952}}{34}$
	$=$	$\frac{- 30 \pm \sqrt{- 52}}{34}$

${((\begin{array}{c} 2 \\ 0 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 2 \\ - 4 \\ - 4 \end{array}) - (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}))}^{2}$	$=$	$11$
	↓	Fasse zusammen.
${((\begin{array}{c} - 1 \\ 1 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ - 4 \\ - 4 \end{array}))}^{2}$	$=$	$11$
	↓	Vereinfache weiter.
${(\begin{array}{c} - 1 + 2 t \\ 1 - 4 t \\ 3 - 4 t \end{array})}^{2}$	$=$	$11$
	↓	Rechne das Skalarprodukt aus.
$(- 1 + 2 t)^{2} + (1 - 4 t)^{2} + (3 - 4 t)^{2}$	$=$	$11$
	↓	Löse die Klammern auf und vergiss dabei nicht die binomische Formel anzuwenden.
$1 - 4 t + 4 t^{2} + 1 - 8 t + 16 t^{2} + 9 - 24 t + 16 t^{2}$	$=$	$11$
	↓	Fasse die linke Seite zusammen.
$36 t^{2} - 36 t + 11$	$=$	$11$	$- 11$
$36 t^{2} - 36 t$	$=$	$0$	$36 t ausklammern$
$36 t \cdot (t - 1)$	$=$	$0$

$E_{T_{1}} : (\vec{x} - \vec{b}) \circ (\vec{b} - \vec{m})$	$=$	$0$
	↓	Setze für $B$ die Koordinaten des ersten Schnittpunktes $S_{1} (2 \| 0 \| 5)$ ein. Setze den Mittelpunkt $M (3 \| - 1 \| 2)$ ein.
$(\vec{x} - (\begin{array}{c} 2 \\ 0 \\ 5 \end{array})) \circ ((\begin{array}{c} 2 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}))$	$=$	$0$
	↓	Vereinfache.
$(\vec{x} - (\begin{array}{c} 2 \\ 0 \\ 5 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$	$=$	$0$
	↓	Diese Gleichung ist die Normalengleichung der Ebene.
$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 2 \\ 0 \\ 5 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$	$=$	$0$
	↓	Vereinfache
$(\begin{array}{c} x_{1} - 2 \\ x_{2} - 0 \\ x_{3} - 5 \end{array}) \circ (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$	$=$	$0$
	↓	Um die Koordinatengleichung zu erhalten, rechne das Skalarprodukt aus.
$(x_{1} - 2) \cdot (- 1) + x_{2} \cdot 1 + (x_{3} - 5) \cdot 3$	$=$	$0$
	↓	Löse die Klammern auf.
$- x_{1} + 2 + x_{2} + 3 x_{3} - 15$	$=$	$0$
	↓	Vereinfache.
$- x_{1} + x_{2} + 3 x_{3} - 13$	$=$	$0$

$E_{T_{1}} : (\vec{x} - \vec{b}) \circ (\vec{b} - \vec{m})$	$=$	$0$
	↓	Setze für $B$ die Koordinaten des zweiten Schnittpunktes $S_{2} (4 \| - 4 \| 1)$ ein. Setze den Mittelpunkt $M (3 \| - 1 \| 2)$ ein.
$(\vec{x} - (\begin{array}{c} 4 \\ - 4 \\ 1 \end{array})) \circ ((\begin{array}{c} 4 \\ - 4 \\ 1 \end{array}) - (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}))$	$=$	$0$
	↓	Vereinfache.
$(\vec{x} - (\begin{array}{c} 4 \\ - 4 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$	$=$	$0$
	↓	Diese Gleichung ist die Normalengleichung der Ebene.
$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 4 \\ - 4 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$	$=$	$0$
	↓	Vereinfache.
$(\begin{array}{c} x_{1} - 4 \\ x_{2} + 4 \\ x_{3} - 1 \end{array}) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$	$=$	$0$
	↓	Um die Koordinatengleichung zu erhalten, rechne das Skalarprodukt aus.
$(x_{1} - 4) \cdot 1 + (x_{2} + 4) \cdot (- 3) + (x_{3} - 1) \cdot (- 1)$	$=$	$0$
	↓	Löse die Klammern auf.
$x_{1} - 4 - 3 x_{2} - 12 - x_{3} + 1$	$=$	$0$
	↓	Vereinfache.
$x_{1} - 3 x_{2} - x_{3} - 15$	$=$	$0$

$(I I) : x_{1} - 3 x_{2} - x_{3}$	$=$	$15$
	↓	Setze $x_{2} = - 14 + s$ und $x_{3} = s$ ein.
$x_{1} - 3 \cdot (- 14 + s) - s$	$=$	$15$
	↓	Löse die Klammer auf.
$x_{1} + 42 - 3 s - s$	$=$	$15$
	↓	Vereinfache.
$x_{1} + 42 - 4 s$	$=$	$15$	$- 42 + 4 s$
$x_{1}$	$=$	$- 27 + 4 s$

$\cos α$	$=$	$\frac{\| (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array}) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array}) \|}{\sqrt{11} \cdot \sqrt{11}}$
	↓	Berechne das Skalarprodukt und vereinfache.
	$=$	$\frac{\| - 1 - 3 - 3 \|}{11}$
	↓	Vereinfache.
	$=$	$\frac{\| - 7 \|}{11}$
	↓	Berechne den Betrag.
	$=$	$\frac{7}{11}$

$D$	$=$	$(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26$
	↓	Setze für $y$ den Wert $0$ ein.
	$=$	$(40 + 4 \cdot 0)^{2} - 4 \cdot (17 + 0^{2}) \cdot 26$
	↓	Vereinfache.
	$=$	$1600 - 1768$
	$=$	$- 168$

$D$	$=$	$(40 + 4 y)^{2} - 4 \cdot (17 + y^{2}) \cdot 26$
	↓	Setze für $y$ den Wert $2$ ein.
	$=$	$(40 + 4 \cdot 2)^{2} - 4 \cdot (17 + 2^{2}) \cdot 26$
	↓	Vereinfache.
	$=$	$48^{2} - 4 \cdot 21 \cdot 26$
	$=$	$2304 - 2184$
	$=$	$120$

Aufgaben zu Kugeln und Geraden

Aufstellen der Kugelgleichung

Gerade g in K einsetzen

Schnittpunkte berechnen

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Gerade g in K einsetzen

Schnittpunktberechnung

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Gerade g in K einsetzen

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Schnittpunkte berechnen

Hast du eine Frage oder Feedback?

Aufstellen der Tangentialebenengleichung im Punkt S1

Aufstellen der Tangentialebenengleichung im Punkt S2

Hast du eine Frage oder Feedback?

Schnitt von ET1 und ET2

Berechnung der Schnittgeraden

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Berührpunkte berechnen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gerade g in $K$ einsetzen

Gerade g in $K$ einsetzen

Gerade g in $K$ einsetzen

Aufstellen der Tangentialebenengleichung im Punkt $S_{1}$

Aufstellen der Tangentialebenengleichung im Punkt $S_{2}$

Schnitt von $E_{T_{1}}$ und $E_{T_{2}}$