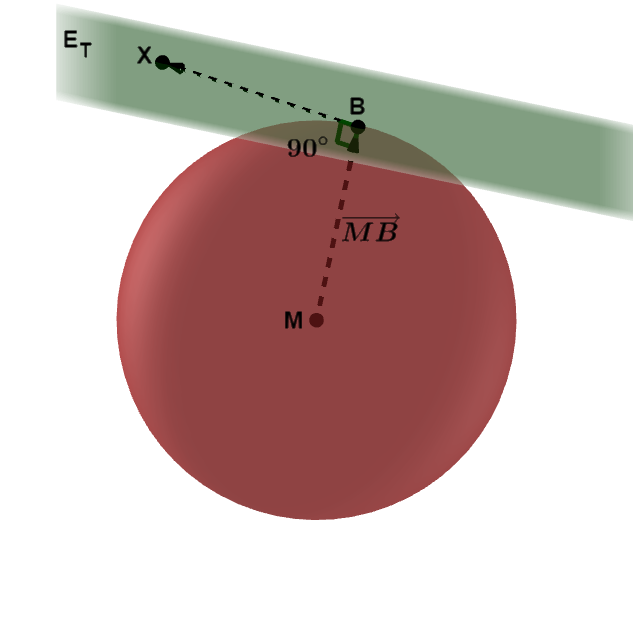
Eine Tangentialebene ist eine Ebene, die eine Kugel in einem Punkt "berührt". Die Kugel und die Tangentialebene haben genau diesen Punkt gemeinsam. Der gemeinsame Punkt heißt Berührpunkt und wird hier mit bezeichnet. ist die Bezeichnung für die Tangentialebene.
Der Vektor vom Mittelpunkt der Kugel zum Berührpunkt ist der Normalenvektor der Tangentialebene , d.h. er steht senkrecht auf ihr.
Der Vektor zeigt vom Berührpunkt zu einem beliebigen Punkt in der Ebene .
Der Vektor steht senkrecht auf dem Vektor , d.h. .
Schreibt man die beiden Verbindungsvektoren als Differenz, so erhält man für die Tangentialebene die Gleichung
Die Gleichung einer Tangentialebene an eine Kugel mit dem Mittelpunkt , dem Radius und einem Punkt auf der Kugel lautet:
Musterbeispiel
Gegeben sind von einer Kugel der Kugelmittelpunkt und der Kugelradius . Wie lautet die Gleichung einer Tangentialebene in Koordinatenform, die die Kugel im Punkt berührt?
Lösung:
Setze in die Tangentialebenengleichung für den Vektor die Koordinaten des Berührpunktes und für die Koordinaten des Mittelpunktes ein. Der Vektor bleibt dabei als Variable erhalten. (Der Kugelradius spielt bei der Lösung dieser Aufgabe keine Rolle!)
| ↓ | Setze und ein. | ||
| ↓ | Vereinfache. | ||
| ↓ | Diese Gleichung ist die Normalengleichung der Ebene. | ||
| ↓ | Fasse zusammen. | ||
| ↓ | Um die Koordinatengleichung zu erhalten, rechne das Skalarprodukt aus. | ||
| ↓ | Löse die Klammern auf. | ||
| ↓ | Vereinfache. | ||
| ↓ | Vereinfache. | ||
Antwort: Die Gleichung der Tangentialebene lautet
.
Übungsaufgaben
Laden
Laden
Laden
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Kugeln in der analytischen Geometrie
- Lagebeziehungen zwischen Kugeln und Punkten
- Lagebeziehung zwischen Kugeln und Geraden
- Lagebeziehung zwischen Kugeln und Ebenen
- Kugel und Tangentialkegel
- Gegenseitige Lage von zwei Kugeln
- Zwei Kugeln mit gemeinsamen äußeren Berührpunkt
- Zwei Kugeln mit gemeinsamen inneren Berührpunkt
- Zwei sich schneidende Kugeln
