🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Lagebeziehung zwischen Kugeln und Ebenen

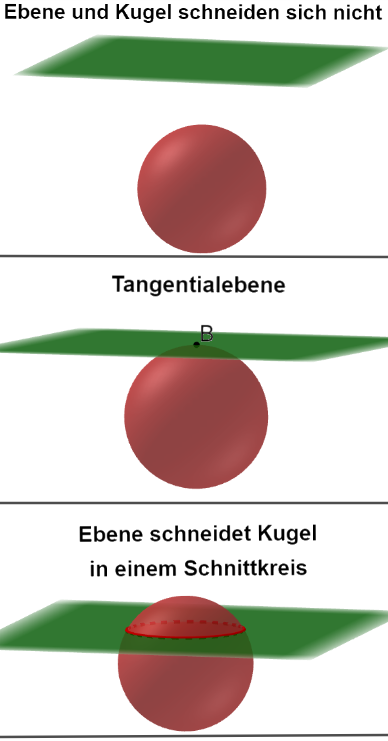
Schnitt einer Kugel mit einer Ebene, 3 Varianten

Es wird die Lage einer Ebene EE bezüglich einer Kugel KK untersucht.

Dabei treten drei Fälle auf:

  • die Ebene schneidet die Kugel nicht (oberes Bild)

  • die Ebene berührt die Kugel in genau einem Punkt, die Ebene ist eine Tangentialebene (mittleres Bild)

  • die Ebene schneidet die Kugel in einem Kreis (unteres Bild)

Allgemeines Vorgehen

Die Kugel ist gegeben durch ihren Mittelpunkt M(m1∣m2∣m3)M(m_1|m_2|m_3) und den Radius r r. Die Ebene EE liegt in der Koordinatenform vor.

Die Ermittlung der Lage von Ebene zu Kugel erfolgt über die Berechnung des Abstandes des Kugelmittelpunktes MM von der Ebene EE. Stelle dazu die Hessesche Normalenform der Ebene EE auf.

Setze die Koordinaten des Kugelmittelpunktes ein:

Nun sind drei Fälle möglich:

  • d(M,E)>rd(M,E)>r; die Ebene schneidet die Kugel nicht

  • d(M,E)=rd(M,E)=r; die Ebene ist eine Tangentialebene

  • d(M,E)<rd(M,E)<r; die Ebene schneidet die Kugel in einem Kreis

Wenn du bei deiner Rechnung festgestellt hast, dass d(M,E)>rd(M,E)>r ist, dann gibt es nichts weiter zu rechnen. Die Ebene schneidet die Kugel nicht.

Ist dagegen d(M,E)=rd(M,E)=r, so kannst du noch den Berührpunkt zwischen der Ebene und der Kugel berechnen. (Beispiel 11)

Ist dagegen d(M,E)<rd(M,E)<r, so kannst du die Koordinaten des Schnittkreismittelpunktes M′M' und den Schnittkreisradius r′r' berechnen. (Beispiel 22)

Beispiel 1

Zeige, dass die Ebene E:  −2x1+2x2−x3=26E:\; -2x_1+2x_2-x_3=26 eine Tangentialebene an die Kugel KK mit dem Mittelpunkt M(2∣2∣1)M(2|2|1) und dem Radius r=9r=9 ist. Berechne auch den Berührpunkt BB.

Lösung:

Stelle die Hessesche Normalenform der Ebene EE auf.

EHNF:  −2x1+2x2−x3−26(−2)2+22+12\displaystyle E_{HNF}: \;\dfrac{-2x_1+2x_2-x_3-26}{\sqrt{(-2)^2+2^2+1^2}}==0\displaystyle 0
↓

Berechne die Wurzel.

EHNF:  −2x1+2x2−x3−263\displaystyle E_{HNF}: \;\dfrac{-2x_1+2x_2-x_3-26}{3}==0\displaystyle 0

Berechne den Abstand des Mittelpunktes MM von der Ebene EE, indem du die Koordinaten von MM in die Hessesche Normalenform einsetzt.

d(M,E)\displaystyle d(M,E)==∣−2⋅2+2⋅2−1⋅1−263∣\displaystyle \left|\dfrac{-2\cdot2+2\cdot2-1\cdot1-26}{3}\right|
↓

vereinfache

==∣−273∣\displaystyle \left|\dfrac{-27}{3}\right|
↓

Berechne den Betrag

==9\displaystyle 9

Der Abstand des Mittelpunktes MM von der Ebene EE ist d=9d=9. Der Kugelradius ist r=9 r=9. Da d=rd=r ist, handelt es sich um eine Tangentialebene.

Berechnung des Berührpunktes

Kugel mit Ebene und Lotgerade

Stelle die Gleichung der Lotgeraden gLotg_{Lot} durch den Mittelpunkt auf die Ebene EE auf.

Verwende als Aufpunkt den Mittelpunkt MM und als Richtungsvektor den Normalenvektor der Ebene EE.

gLot:  X⃗=(221)+t⋅(−22−1)g_{Lot}:\;\vec X=\begin{pmatrix}2\\2\\1\end{pmatrix}+t\cdot\begin{pmatrix} -2 \\2 \\-1 \end{pmatrix}

oder

gLot:  X⃗=( x1x2 x3)=( 2−2t2+2t 1−t)g_{Lot}:\;\vec X=\begin{pmatrix}\textcolor{006400}{ x_1}\\\textcolor{ff6600}{ x_2}\\\textcolor{660099}{  x_3}\end{pmatrix}=\begin{pmatrix}\textcolor{006400}{  2-2t}\\\textcolor{ff6600}{ 2+2t}\\\textcolor{660099}{  1-t}\end{pmatrix}

Berechne den Berührpunkt, indem du die Lotgerade gLotg_{Lot} mit der Ebene EE schneidest.

gLot∩Eg_{Lot}\cap E

↓
E:  −2x1+2x2−x3\displaystyle E:\;-2\textcolor{006400}{x_1}+2\textcolor{ff6600}{ x_2}-\textcolor{660099}{x_3}==26\displaystyle 26
↓

Setze x1=2−2t\textcolor{006400}{x_1=2-2t}, x2=2+2t\textcolor{ff6600}{ x_2=2+2t}, x3=1−t\textcolor{660099}{x_3=1-t} in E E ein.

−2⋅(2−2t)+2⋅(2+2t)−1⋅(1−t)\displaystyle -2\cdot(\textcolor{006400}{2-2t})+2\cdot(\textcolor{ff6600}{ 2+2t})-1\cdot(\textcolor{660099}{1-t})==26\displaystyle 26
↓

Löse die Klammern auf.

−4+4t+4+4t−1+t\displaystyle -4+4t+4+4t-1+t==26\displaystyle 26
↓

Vereinfache die linke Seite.

9t−1\displaystyle 9t-1==26\displaystyle 26+1\displaystyle +1
↓

Löse nach tt auf.

9t\displaystyle 9t==27\displaystyle 27:9\displaystyle :9
t\displaystyle t==3\displaystyle 3

Zur Berechnung des Berührpunktes setzt du t=3t=3 in die Gleichung der Lotgeraden ein.

X⃗B=(221)+3⋅(−22−1)=(2−62+61−3)=(−48−2)\vec X_B=\begin{pmatrix}2\\2\\1\end{pmatrix}+3\cdot\begin{pmatrix} -2 \\2 \\-1 \end{pmatrix}=\begin{pmatrix}2-6\\2+6\\1-3\end{pmatrix}=\begin{pmatrix}-4\\8\\-2\end{pmatrix}

Antwort: Der Berührpunkt hat die Koordinaten B(−4∣8∣−2)B(-4|8|-2).

Beispiel 2

Zeige, dass die Ebene E:  x1+2x2+2x3=2E:\; x_1+2x_2+2x_3=2 die Kugel KK mit dem Mittelpunkt M(3∣0∣1)M(3|0|1) und dem Radius r=5r=5 schneidet. Berechne auch den Schnittkreismittelpunkt M′M' und den Schnittkreisradius r′r'.

Lösung:

Stelle die Hessesche Normalenform der Ebene EE auf.

EHNF:  x1+2x2+2x3−212+22+22\displaystyle E_{HNF}: \;\dfrac{x_1+2x_2+2x_3-2}{\sqrt{1^2+2^2+2^2}}==0\displaystyle 0
↓

Berechne die Wurzel.

EHNF:  x1+2x2+2x3−23\displaystyle E_{HNF}: \;\dfrac{x_1+2x_2+2x_3-2}{3}==0\displaystyle 0

Berechne den Abstand des Mittelpunktes MM von der Ebene EE, indem du die Koordinaten von MM in die Hessesche Normalenform einsetzt.

d(M,E)\displaystyle d(M,E)==∣1⋅3+2⋅0+2⋅1−23∣\displaystyle \left|\dfrac{1\cdot3+2\cdot0+2\cdot1-2}{3}\right|
↓

vereinfache

==∣33∣\displaystyle \left|\dfrac{3}{3}\right|
↓

Berechne den Betrag

==1\displaystyle 1

Der Abstand des Mittelpunktes MM von der Ebene EE ist d=1d=1. Der Kugelradius ist r=5 r=5. Da d<rd<r ist, wird die Kugel in einem Kreis geschnitten.

Berechnung des Schnittkreismittelpunktes M′M'

Schnittkreisradius

Den Mittelpunkt M′M' des Schnittkreises berechnest du, indem du die Lotgerade von MM auf die Ebene EE mit der Ebene EE schneidest.

Berechne die Gleichung der Lotgeraden gLotg_{Lot} durch den Mittelpunkt auf die Ebene EE. Verwende als Aufpunkt den Mittelpunkt MM und als Richtungsvektor den Normalenvektor der Ebene EE.

gLot:  X⃗=(301)+t⋅(122)=(3+t2t1+2t)g_{Lot}:\;\vec X=\begin{pmatrix}3\\0\\1\end{pmatrix}+t\cdot\begin{pmatrix} 1 \\2 \\2 \end{pmatrix}=\begin{pmatrix}\textcolor{006400}{ 3+t} \\\textcolor{ff6600}{ 2t} \\\textcolor{660099}{1+2t} \end{pmatrix}

Schneide die Lotgerade mit der Ebene: gLot∩Eg_{Lot}\cap E

E:  x1+2x2+2x3\displaystyle E:\; \textcolor{006400}{ x_1}+2\textcolor{ff6600}{ x_2}+2\textcolor{660099}{x_3}==2\displaystyle 2
↓

Setze gg in EE ein.

1⋅(3+t)+2⋅(2t)+2⋅(1+2t)\displaystyle 1\cdot(\textcolor{006400}{ 3+t})+2\cdot(\textcolor{ff6600}{ 2t})+2\cdot(\textcolor{660099}{1+2t})==2\displaystyle 2
↓

Löse die Klammern auf.

3+t+4t+2+4t\displaystyle 3+t+4t+2+4t==2\displaystyle 2
↓

Vereinfache die linke Seite.

9t+5\displaystyle 9t+5==2\displaystyle 2−5\displaystyle -5
↓

Löse nach t auf.

9t\displaystyle 9t==−3\displaystyle -3:9\displaystyle :9
t\displaystyle t==−39\displaystyle -\dfrac{3}{9}
↓

Kürze den Bruch.

t\displaystyle t==−13\displaystyle -\dfrac{1}{3}

Zur Berechnung des Schnittpunktes M′M' setzt du t=−13t=-\dfrac{1}{3} in die Gleichung der Lotgeraden ein.

X⃗M′=(301)−13⋅(122)=(3−130−231−23)=(83−2313)\vec X_{M'}=\begin{pmatrix}3\\0\\1\end{pmatrix}-\dfrac{1}{3}\cdot\begin{pmatrix} 1 \\2 \\2 \end{pmatrix}=\begin{pmatrix}3-\dfrac{1}{3}\\[2ex]0-\dfrac{2}{3}\\[2ex]1-\dfrac{2}{3}\end{pmatrix}=\begin{pmatrix}\dfrac{8}{3}\\[2ex]-\dfrac{2}{3}\\[2ex]\dfrac{1}{3}\end{pmatrix}

Antwort: Der Mittelpunkt M′M' des Schnittkreises hat die Koordinaten:

M′(83∣−23∣13)M'\left(\dfrac{8}{3}\Big\vert-\dfrac{2}{3}\Big\vert\dfrac{1}{3}\right).

Berechnung des Schnittkreisradius r′r'

Den Schnittkreisradius r′r' kannst du mithilfe des Satzes von Pythagoras berechnen (siehe obige Abbildung). Der Abstand der Ebene EE vom Mittelpunkt MM ist d=1d=1 (wurde am Anfang berechnet) und der Kugelradius ist r=5r=5.

r2\displaystyle r^2==d2+r′2\displaystyle d^2+r'^2
↓

Nach r′r' auflösen.

r′\displaystyle r'==r2−d2\displaystyle \sqrt{r^2-d^2}
↓

Setze r=5r=5 und d=1 d=1 ein.

==52−12\displaystyle \sqrt{5^2-1^2}
↓

vereinfache

==24\displaystyle \sqrt{24}
≈≈4,9\displaystyle 4{,}9

Antwort: Der Radius r′r' des Schnittkreises beträgt 24≈4,9  LE\sqrt{24}\approx 4{,}9\; \text{LE}.

Übungsaufgaben

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?