Inhalt dieses Artikels ist
die Berechnung von Parabeltangenten durch eine Schnittbedingung,
die Berechnung mithilfe der Ableitung,
eine Konstruktion von Parabeltangenten,
ein Hinweis auf die Bedeutung von Tangenten im Alltag.
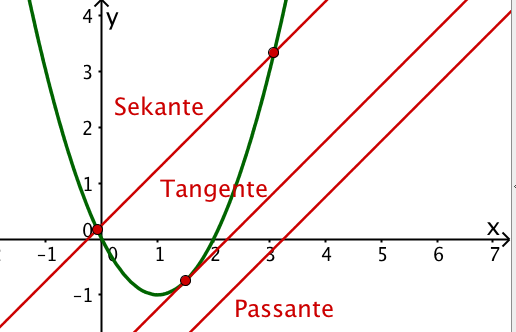
Eine Tangente (von lateinisch "tangere" = "berühren") an eine Parabel ist eine Gerade mit zwei kennzeichnenden Eigenschaften:
sie ist nicht zur y-Achse parallel und hat mit der Parabel als Schnittbedingung genau einen Punkt (Berührpunkt) gemeinsam.
ihre Steigung ist der Ableitungswert der Parabel im Berührpunkt.
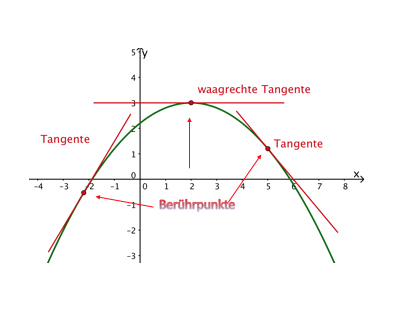
Berechnung von Parabeltangenten durch die Schnittbedingung
Beispiel
Berechne die Tangente an die Parabel im Kurvenpunkt .
Vorbereitungen:
Überzeuge dich durch Einsetzen seiner Koordinaten in die Parabelgleichung, dass der Punkt A auf der Parabel liegt.
Die gesuchte Gerade heiße . Ihre Steigung und ihr y-Achsenabschnitt sind noch unbekannte Parameter.
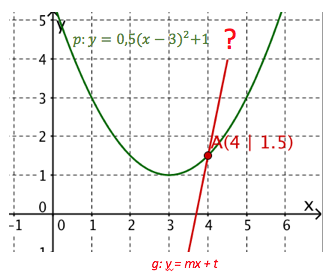
Schneide den Graphen der Parabel p mit einer Geraden g indem du die Funktionsterme gleichsetzt.
Bringe alles auf eine Gleichungsseite und ordne die quadratische Gleichung.
Mit der Gleichung berechnest du die x-Koordinate eventuell vorhandener Schnittpunkte.
Jetzt kommt das Wesentliche der Tangentenberechnung:
Da die gesuchte Tangente genau einen Punkt mit der Parabel gemeinsam hat, darf diese quadratische Gleichung - neben dem x-Wert von A - keine weitere Lösung haben. Also muss ihre Diskriminante Null sein!
Bilde die Diskriminante der quadratischen Gleichung und setze sie gleich Null.
Die Gleichung enthält noch beide Unbekannte und .
Setze jetzt die Koordinaten des Punktes in die Geradengleichung ein und löse nach t auf.
Setze t in die Diskriminantengleichung ein, ordne die Gleichung und löse sie z. B. mit der Mitternachtsformel oder zweiten binomischen Formel.
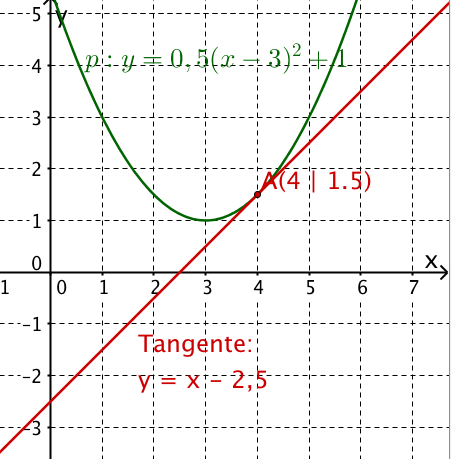
Setze in ein und gib die Tangentengleichung an.
gesuchte Tangente:
Beispiel
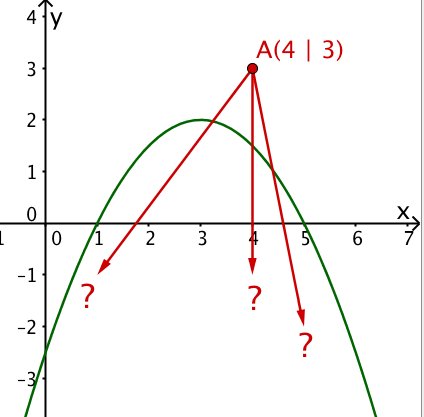
Lege vom Punkt A(4|3) aus Tangenten an die Parabel und berechne die Koordinaten vorhandener Berührpunkte.
Vorbereitungen:
Überzeuge dich durch Einsetzen der x-Koordinate von A in die Parabelgleichung, dass der Punkt A außerhalb der Parabel liegt: Es gilt .
Die gesuchten Geraden haben die Funktionsgleichung .
Schneide den Graphen der Parabel mit einer Geraden g indem du die Funktionsterme gleichsetzt.
Bringe alles auf eine Gleichungsseite, ordne die quadratische Gleichung.
Mit der Gleichung (*) berechnest du die x-Koordinaten eventuell vorhandener Schnittpunkte.
Jetzt kommt das Wesentliche der Tangentenberechnung:
Jede Gerade, die vom Punkt A ausgeht darf mit der Parabel nur einen Punkt gemeinsam haben. Also darf die quadratische Gleichung nur eine Lösung haben. D.h. ihre Diskriminante muss Null sein.
Bilde die Diskrimante der quadratischen Gleichung und setze sie Null.
Die Gleichung enthält noch die beiden Unbekannten und .
Setze jetzt die Koordinaten des Punktes in die Geradengleichung und löse nach t auf.
Setze t in die Diskriminantengleichung ein, ordne sie und löse die Gleichung z.B. mit der Mitternachtsformel.
Die Gleichung hat zwei Lösungen. Es gibt also zwei Geraden, die den Punkt A enthalten und Tangenten an die Parabel sind.
Setze jeden der beiden Steigungswerte in die Gleichung ein, um den zugehörigen y-Achsenabschnitt zu bekommen.
Gib die beiden Tangentengleichungen an.
Tangente:
Tangente:
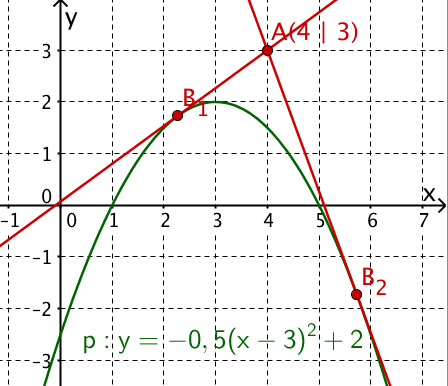
Die Berührpunkte und der beiden Tangenten mit der Parabel berechnest du mit der Schnittgleichung (*):
Da es sich um Tangenten handelt, ist die Diskriminante der Schnittgleichung in beiden Fällen gleich Null.
Die Mitternachtsformel ergibt also:
Berührpunkt :
Setze um die x-Koordinate von zu erhalten. Setze den erhaltenen Wert in die Tangentengleichung (oder Parabelgleichung) ein, um die y-Koordinate zu berechnen.
Damit gilt:
Gerundet:
Berührpunkt
Setze um die x-Koordinate von zu erhalten. Setze den erhaltenen Wert in die Tangentengleichung (oder Parabelgleichung) ein, um die y-Koordinate zu berechnen.
Damit gilt:
Gerundet:
Berechnung von Parabeltangenten mithilfe der Ableitung
Beispiel
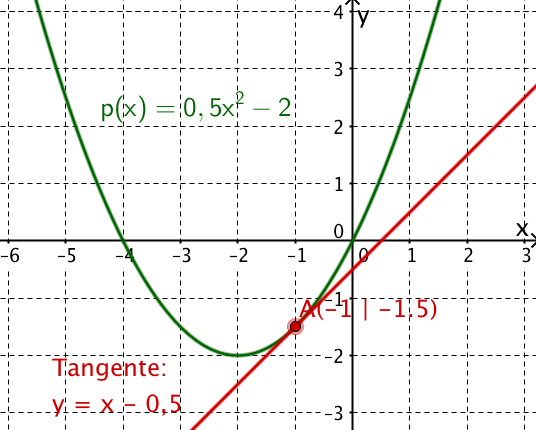
Berechne die Tangente an die Parabel im Punkt mithilfe der Ableitung.
Vorbereitungen:
Überzeuge dich durch Einsetzen der x-Koordinate von A in die Parabelgleichung, dass der Punkt A auf der Parabel liegt.
Die gesuchte Gerade habe die Gleichung . Ihre Steigung und ihr y-Achsenabschnitt sind noch unbekannte Parameter.
Berechne die Ableitung der Parabel.
Die Steigung m der gesuchten Tangente ist der Ableitungswert der Parabel im Berührpunkt . Setze also in ein. Dies ergibt .
Setze jetzt und die beiden Koordinaten von in die Geradengleichung ein und löse nach auf.
Gib die Tangentengleichung an.
Tangente:
Beispiel
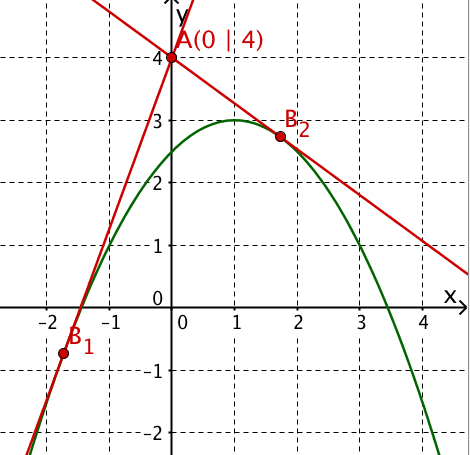
Lege mithilfe der Ableitung vom Punkt aus Tangenten an die Parabel und berechne die Koordinaten vorhandener Berührpunkte.
Vorbereitungen:
Überzeuge dich durch Einsetzen der x-Koordinate des Punktes in die Parabelgleichung, dass außerhalb der Parabel liegt.
Benutze die Tangentengleichung
Wähle einen beliebigen Punkt der Parabel und stelle für diesen die Tangentengleichung auf, in die die Werte für und eingesetzt werden.
Die Tangente soll durch den Punkt verlaufen. Dessen Koordinaten also in die Gleichung einsetzen.
Ordne die quadratische Gleichung.
Setze die beiden gefundenen Werte in g(x) ein um die Tangentengleichungen zu erhalten.
Setze in die Gleichung der 1.Tangente ein, um die 2. Koordinate des Berührpunktes zu erhalten.
Setze entsprechend in die Gleichung der 2.Tangente ein, um die 2. Koordinate des Berührpunktes zu erhalten.
Tangente:
Tangente:
Berührpunkte
gerundet:
gerundet:
Die Konstruktion von Parabeltangenten
Unter einer Konstruktion versteht man das Zeichnen eines geometrischen Objektes (Strecke, Gerade, Lot, Parallele, Winkel etc.) mithilfe von Zirkel und Lineal. Oft ist auch ein Geodreieck zugelassen.
Bekannt ist die Konstruktion der Tangente an einen Kreis. Man erhält sie als Lot auf den Radius im Berührpunkt.
So konstruiert man die Tangente an eine Parabel im Berührpunkt :
Wähle zwei weitere Parabelpunkte und so, dass hinsichtlich der x-Koordinaten der drei Punkte Mittelpunkt ist.
Das heißt, es gilt:
Die Parallele zur Geraden durch den Berührpunkt ist die gesuchte Tangente.
ist ein beliebiger Wert.
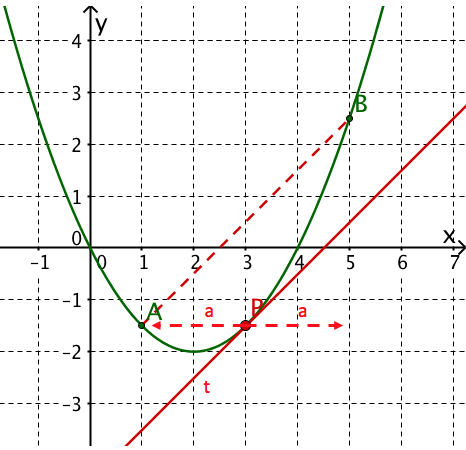
Überzeuge dich anhand des Applets von der Tangentenkonstruktion. Du kannst den Berührpunkt verschieben und für verschiedene Werte wählen.
Bedeutung von Tangenten im Alltag
In Situationen wie diesen sind Tangenten bedeutsam:
wenn ein Sprinter beim Kurvenlauf aus der Bahn kommt,
wenn ein Eisschnelläufer in der Kurve ausgleitet,
wenn ein Auto in einer Kurve plötzlich auf eine Glatteisstelle gerät und jeden Halt verliert.
Ohne Einwirkung weiterer äußerer Kräfte bewegen sich die Körper im Anschluss an das Geschehen in "tangentialer Richtung" zur Kurve.

Beispiel
Ein Auto durchfährt mit hoher Geschwindigkeit die parabelförmige Straßenführung in Richtung zunehmender x-Werte.
An der Glatteisstelle verliert es jeden Halt.
Berechne, ob ihm - ohne Einfluss weiterer äußerer Kräfte - an der Stelle möglicherweise ein Baum im Wege steht.
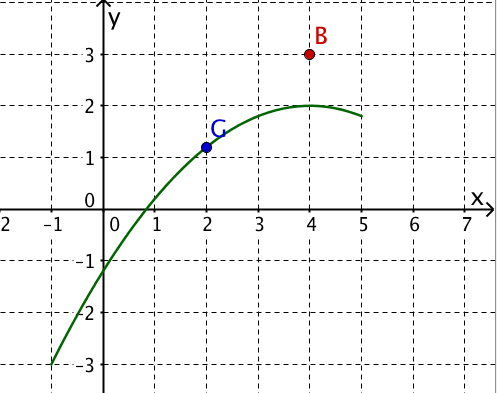
Die mathematische Untersuchung der gefährlichen Situation ist die Beantwortung der Frage, ob die Tangente an die Parabel im Punkt durch den Punkt verläuft.
Gegeben ist:
Bilde und berechne die 2. Koordinaten von G und .
Stelle die Tangentengleichung auf.
in t einsetzen und entscheiden
Wenn keine weiteren Kräfte mehr auftreten, wird das Auto nicht gegen den Baum prallen.
