Kugeln in der analytischen Geometrie

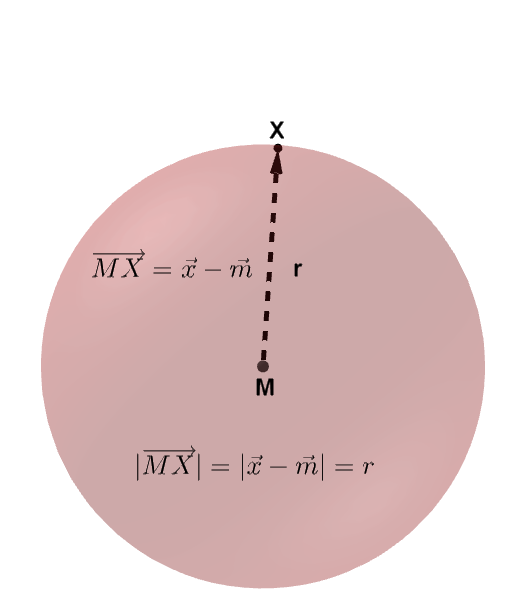
Die Koordinaten des Kugelmittelpunktes $M$ und der Kugelradius $r$ definieren eine Kugel im Raum. Die Oberfläche der Kugel ist der geometrische Ort aller Punkte $X$ , die vom Mittelpunkt $M$ den gleichen Abstand $r$ haben.

Herleitung der Koordinantegleichung der Kugel

Der Vektor $\overrightarrow{MX}=\vec x-\vec m$ hat demnach immer den Betrag r.

Alle Punkte auf der Kugeloberfläche erfüllen die Gleichung

$K:\ |\vec{x}-\vec{m}|=r$ .

Äquivalent dazu ist die Gleichung

$K:\ (\vec{x}-\vec{m})^2=r^2$

oder

$K:\ (\vec{x}-\vec{m})\circ (\vec{x}-\vec{m})=r^2$

Die Kugelgleichung kann auch als Koordinatengleichung angegeben werden:

$K:\ (\vec{x}-\vec{m})\circ (\vec{x}-\vec{m})=r^2\;\;\Rightarrow\;\;\left(\begin{pmatrix} x_1 \\x_2 \\ x_3 \end{pmatrix}-\begin{pmatrix} m_1 \\m_2 \\ m_3 \end{pmatrix}\right)^2=r^2$

$K:\ \begin{pmatrix} x_1-m_1 \\x_2-m_2 \\ x_3-m_3 \end{pmatrix}^2=r^2\;\;\Rightarrow\;\;\begin{pmatrix} x_1-m_1 \\x_2-m_2 \\ x_3-m_3 \end{pmatrix}\circ \begin{pmatrix} x_1-m_1 \\x_2-m_2 \\ x_3-m_3 \end{pmatrix}=r^2$

Nach Berechnung des Skalarproduktes erhältst du die Koordinatengleichung der Kugel.

\displaystyle K:\ (x_1-m_1)^2+(x_2-m_2)^2+(x_3-m_3)^2=r^2

Beispiel

Gegeben sind von einer Kugel der Kugelmittelpunkt $\textcolor{ff6600}{M(-1|7|3)}$ und der Kugelradius $\textcolor{006400}{r=5}$ . Wie lautet die Vektorgleichung und die Koordinatengleichung dieser Kugel?

Lösung

Setze die gegebenen Werte $\textcolor{ff6600}{M(-1|7|3)}$ und $\textcolor{006400}{r=5}$ in die Kugelgleichung ein:

$\displaystyle (\vec{x}-\vec{\textcolor{ff6600}{m}})^2$	$=$	$\displaystyle \textcolor{006400}{r}^2$
	↓	Setze $\textcolor{ff6600}{M}$ und $\textcolor{006400}{r}$ ein.
$\displaystyle \left(\vec x-\textcolor{ff6600}{\begin{pmatrix} -1 \\7 \\ 3 \end{pmatrix}}\right)^2$	$=$	$\displaystyle \textcolor{006400}{5}^2$
	↓	Berechne auf der rechten Seite das Quadrat.
$\displaystyle \left(\vec x-\begin{pmatrix} -1 \\7 \\ 3 \end{pmatrix}\right)^2$	$=$	$\displaystyle 25$

Du hast nun die Vektorgleichung der Kugel aufgestellt. Für die Koordinatengleichung berechnest du das Skalarprodukt.

$\begin{pmatrix} x_1-(-1) \\x_2-7 \\ x_3-3 \end{pmatrix}\circ \begin{pmatrix} x_1-(-1) \\x_2-7 \\ x_3-3 \end{pmatrix}=25\;\;\;\;$

$\Rightarrow\ K:\ (x_1+1)^2+(x_2-7)^2+(x_3-3)^2=25$

Antwort: Die Vektorgleichung lautet $K:\ \left(\vec x-\begin{pmatrix} -1 \\7 \\ 3 \end{pmatrix}\right)^2=25$ und die Koordinatengleichung ist $K:\ (x_1+1)^2+(x_2-7)^2+(x_3-3)^2=25$ .

Übungsaufgaben

Inhalt wird geladen…

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?