Lagebeziehungen zwischen Kugeln und Punkten

Es wird die Lage eines Punktes bezüglich einer Kugel $K$ untersucht.

Dabei treten drei Fälle auf:

der Punkt liegt innerhalb von $K$
der Punkt liegt auf $K$
der Punkt liegt außerhalb von $K$

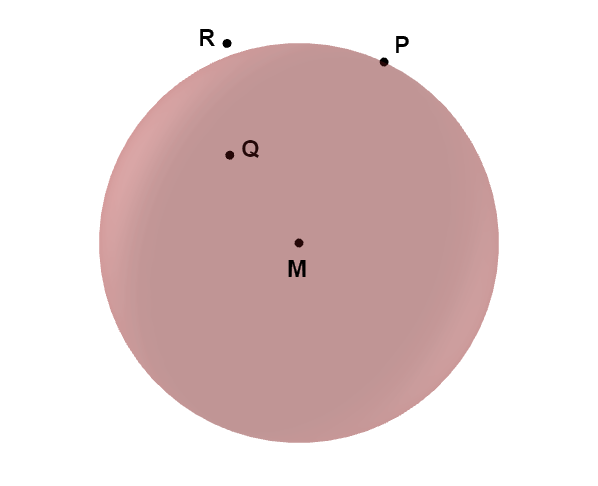
In der Abbildung liegt der Punkt $Q$ innerhalb der Kugel, der Punkt $P$ auf der Kugel und der Punkt $R$ außerhalb der Kugel.

Allgemeines Vorgehen

Gegeben sind eine Kugel $K$ mit dem Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ , dem Radius $r$ und ein Punkt $A (a_{1} | a_{2} | a_{3})$ . Welche Lage hat der Punkt $A$ bezüglich der Kugel $K$ ?

Stelle die Kugelgleichung auf.
	↓
$K : {(\vec{x} - (\begin{array}{c} m_{1} \\ m_{2} \\ m_{3} \end{array}))}^{2}$	$=$	$r^{2}$
	↓	Setze die Punktkoordinaten von $A$ für den Vektor $\vec{x}$ in $K$ ein und prüfe, ob die Gleichung erfüllt ist.
${((\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) - (\begin{array}{c} m_{1} \\ m_{2} \\ m_{3} \end{array}))}^{2}$	$=$	$r^{2}$
	↓	Vereinfache die linke Seite.
${(\begin{array}{c} a_{1} - m_{1} \\ a_{2} - m_{2} \\ a_{3} - m_{3} \end{array})}^{2}$	$=$	$r^{2}$
	↓	Berechne das Skalarprodukt.
$(a_{1} - m_{1})^{2} + (a_{1} - m_{1})^{2} + (a_{1} - m_{1})^{2}$	$=$	$r^{2}$

Nun sind drei Fälle möglich:

die linke Seite der Gleichung ist $< r^{2} \Rightarrow$ der Punkt liegt innerhalb von $K$
die linke Seite der Gleichung ist $= r^{2} \Rightarrow$ der Punkt liegt auf $K$
die linke Seite der Gleichung ist $> r^{2} \Rightarrow$ der Punkt liegt außerhalb von $K$

BeispielPunkt innerhalb einer Kugel

Gegeben ist eine Kugel $K$ mit dem Mittelpunkt $M (3 | 1 | 5)$ und dem Radius $r = 4$ . Untersuche die Lage des Punktes $A (3 | 4 | 5)$ bezüglich der Kugel $K$ .

Lösung:

Stelle die Kugelgleichung auf:

$K : {(\vec{x} - (\begin{array}{c} 3 \\ 1 \\ 5 \end{array}))}^{2} = 4^{2} = 16$

Setze die Punktkoordinaten von $A$ für den Vektor $\vec{x}$ in $K$ ein und prüfe, ob die Gleichung erfüllt ist.

${((\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) - (\begin{array}{c} 3 \\ 1 \\ 5 \end{array}))}^{2}$	$=$	$16$
	↓	Vereinfache die linke Seite.
${(\begin{array}{c} 0 \\ 3 \\ 0 \end{array})}^{2}$	$=$	$16$
	↓	Berechne das Skalarprodukt.
$0 + 3^{2} + 0$	$=$	$16$
$9$	$<$	$16$

Antwort: Der Punkt $A$ erfüllt die Kugelgleichung nicht. Da $9 < 16$ ist, liegt der Punkt $A$ innerhalb der Kugel $K$ .

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?