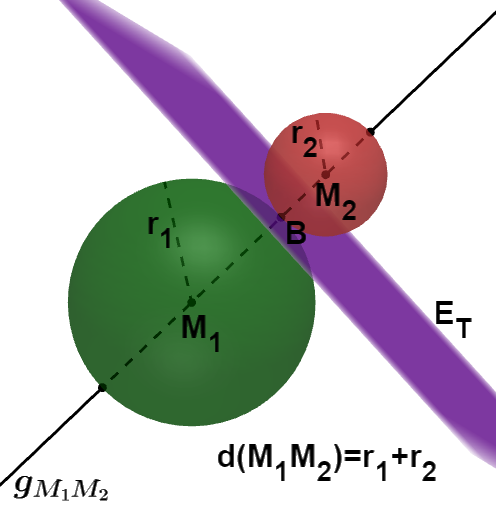
Ist der Abstand der beiden Kugelmittelpunkte gleich der Summe der beiden Kugelradien, dann berühren sich die Kugeln in einem äußeren Punkt .
Die beiden Kugeln haben eine gemeinsame Tangentialebene .
Gesucht sind die Berührpunktkoordinaten und die Gleichung der Tangentialebene.
Allgemeines Vorgehen
Berechnung von
Die Kugel hat den Mittelpunkt und den Radius . Die Kugel hat den Mittelpunkt und den Radius .
Berechne den Vektor und dann seinen Betrag .
Aus der nebenstehenden Abbildung kannst du folgende Vektorgleichung ablesen:
Dabei ist der Vektor ein Einheitsvektor:

Berechnung von
Mit Hilfe des berechneten Einheitsvektors und einem Punkt der Ebene (hier der Berührpunkt ) kann die Gleichung der Tangentialebene erstellt werden. Bei Verwendung von erhältst du die Hessesche Normalenform der Ebene bzw. nach Berechnung des Skalarproduktes eine Koordinatenform.
Beispiel:
Gegeben sind die Kugeln und
Berechne den gemeinsamen Berührpunkt und die Koordinatengleichung der Tangentialebene .
Haben die beiden Kugeln einen gemeinsamen äußeren Berührpunkt?
Berechne den Vektor und dann seinen Betrag .
und
Der Abstand der beiden Kugelmittelpunkte beträgt und die Summe der beiden Kugelradien beträgt auch .
Die beiden Kugeln berühren sich außen.
Berechnung von
Berechne den Vektor :
Dabei ist , und der Einheitsvektor ist .
Antwort: Der Berührpunkt hat die Koordinaten .
Berechnung von
Mit Hilfe des oben berechneten Einheitsvektors und einem Punkt der Ebene (hier der Berührpunkt ) kann die Gleichung der Tangentialebene erstellt werden. Bei Verwendung von erhältst du die Hessesche Normalenform der Ebene bzw. nach Berechnung des Skalarproduktes eine Koordinatenform.
| ↓ | Setze und ein. | ||
| ↓ | Das ist die Hessesche Normalenform der Tangentialebene. | ||
| ↓ | Umwandlung in die Koordinatenform. | ||
| ↓ | Berechne das Skalarprodukt. | ||
| ↓ | Löse die Klammern auf. | ||
| ↓ | Vereinfache. | ||
| ↓ | Vereinfache. | ||
Antwort: Die Hessesche Koordinatenform der Tangentialebene lautet: bzw. Tangentialebene als Koordinatengleichung:
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Kreisen und Kugeln
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Kugeln in der analytischen Geometrie
- Tangentialebene an eine Kugel
- Lagebeziehungen zwischen Kugeln und Punkten
- Lagebeziehung zwischen Kugeln und Geraden
- Lagebeziehung zwischen Kugeln und Ebenen
- Kugel und Tangentialkegel
- Gegenseitige Lage von zwei Kugeln
- Zwei Kugeln mit gemeinsamen inneren Berührpunkt
- Zwei sich schneidende Kugeln
