Aufgaben zu Kugeln, Ebenen und Tangentialebenen

Hier findest du Aufgaben zu Kugeln, Ebenen und Tangentialebenen im dreidimensionalen Koordinatensystem. Lerne, die Gleichungen rechnerisch zu bestimmen.

1
Gegeben sind eine Kugel $K$ mit dem Mittelpunkt $M (8 | 8 | 6)$ und dem Radius $r = 7$ sowie eine Ebene $E : \vec{x} = (\begin{array}{c} 3 \\ 5 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) + s \cdot (\begin{array}{c} 1 \\ - 2 \\ 2 \end{array})$ .
1) Zeige, dass die Ebene $E$ und die Kugel $K$ mehr als einen Punkt gemeinsam haben und berechne den Mittelpunkt $M^{'}$ und den Radius $r_{1}^{'}$ des Schnittkreises.
2) Berechne anschließend $z > 8$ so, dass $P (6 | z | 2)$ auf der Kugeloberfläche liegt.
3) Ermittle die Gleichung der Tangentialebene $T$ , welche die Kugel $K$ im Punkt $P$ berührt, in der Koordinatenform.
4) Bestimme die Gleichung einer zu $T$ parallelen Ebene in Koordinatenform, deren Schnittkreis mit der Kugel den Radius $r_{2}^{'} = 3$ hat.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis und Kugel
Teilaufgabe 1
Bestimmung der Art des Schnitts von Ebene und Kugel
Wandle die Parameterform der Ebene $E$ in eine Koordinatenform um.
$E : \vec{x} = (\begin{array}{c} 3 \\ 5 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) + s \cdot (\begin{array}{c} 1 \\ - 2 \\ 2 \end{array})$
Berechne den Normalenvektor der Ebene $E$ als Kreuzprodukt der beiden Richtungsvektoren.
$\vec{n} = (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) \times (\begin{array}{c} 1 \\ - 2 \\ 2 \end{array}) = (\begin{array}{c} 1 \cdot 2 - 0 \cdot (- 2) \\ 0 \cdot 1 - (- 1) \cdot 2 \\ (- 1) \cdot (- 2) - 1 \cdot 1 \end{array}) = (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$
Wähle einen beliebigen Punkt $A$ mit dem Ortsvektor $\vec{a}$ , der in der Ebene $E$ liegt. Hier z.B. den Aufpunkt der Ebene: $\vec{a} = (\begin{array}{c} 3 \\ 5 \\ 3 \end{array})$
Setze die Vektoren $\vec{n}$ und $\vec{a}$ in die allgemeine Normalenform ein und multipliziere das Skalarprodukt aus:
$E : \vec{n} \circ [\vec{x} - \vec{a}] = 0 \Rightarrow (\begin{array}{c} 2 \\ 2 \\ 1 \end{array}) \circ [\vec{x} - (\begin{array}{c} 3 \\ 5 \\ 3 \end{array})] = 0$
Das Skalarprodukt wird mit Hilfe des Distributivgesetzes ausmultipliziert:
$2 x_{1} + 2 x_{2} + x_{3} - (2 \cdot 3 + 2 \cdot 5 + 1 \cdot 3) = 0 \Rightarrow$
$2 x_{1} + 2 x_{2} + x_{3} - 19 = 0$
Um die Hessesche Normalenform einer Ebene zu berechnen, teilt man die Ebenengleichung in Koordinatenform durch den Betrag des Normalenvektors $| \vec{n} |$ . Der Normalenvektor wurde oben mit Hilfe des Kreuzproduktes berechnet. Wenn die Koordinatengleichung der Ebene gegeben ist, kann der Normalenvektor aus der Koordinatengleichung der Ebene abgelesen werden. Die Koeffizienten in der Ebenengleichung ergeben den Normalenvektor.
$\vec{n} = (\begin{array}{c} 2 \\ 2 \\ 1 \end{array}) \Rightarrow | \vec{n} | = \sqrt{2^{2} + 2^{2} + 1^{2}} = \sqrt{9} = 3$
$H N F : \frac{2 x_{1} + 2 x_{2} + x_{3} - 19}{3} = 0$
Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein:
$\begin{array}{rcl} d (M, E) & = & | \frac{2 \cdot 8 + 2 \cdot 8 + 1 \cdot 6 - 19}{3} | \\ = & | \frac{19}{3} | \\ = & \frac{19}{3} \end{array}$
Der Abstand des Kugelmittelpunktes von der Ebene $E$ beträgt $\frac{19}{3}$ und ist somit kleiner als der Kugelradius $r = 7.$ Die Ebene $E$ schneidet somit die Kugel in einem Schnittkreis.
Antwort: Damit ist gezeigt, dass die Ebene $E$ und die Kugel $K$ mehr als einen Punkt gemeinsam haben.
Berechnung des Mittelpunktes $M^{'}$ des Schnittkreises
Stelle die Gleichung der Lotgeraden von $M$ auf die Ebene $E$ auf, indem du für den Stützvektor den Vektor zum Kugelmittelpunkt und als Richtungsvektor den Normalenvektor der Ebene $E$ verwendest.
$g_{L o t} : \vec{x} = (\begin{array}{c} 8 \\ 8 \\ 6 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$
Schneide $g_{L o t}$ mit der Ebene $E$ :

$\begin{array}{rcl} 2 \cdot (8 + 2 t) + 2 \cdot (8 + 2 t) + 1 \cdot (6 + t) - 19 & = & 0 \\ 16 + 4 t + 16 + 4 t + 6 + t - 19 & = & 0 \\ 9 t & = & - 19 \\ t & = & - \frac{19}{9} \end{array}$
Setze $t = - \frac{19}{9}$ in die Geradengleichung ein und du erhältst den Vektor zum Mittelpunkt $M^{'}$ des Schnittkreises.
$\begin{array}{l} \vec{x_{M^{'}}} = (\begin{array}{c} 8 \\ 8 \\ 6 \end{array}) + (- \frac{19}{9}) \cdot (\begin{array}{c} 2 \\ 2 \\ 1 \end{array}) = (\begin{array}{c} \frac{34}{9} \\ \frac{34}{9} \\ \frac{35}{9} \end{array}) \\ \Rightarrow M^{'} (\frac{34}{9} | \frac{34}{9} | \frac{35}{9}) \end{array}$
Antwort: Der Mittelpunktes $M^{'}$ des Schnittkreises hat folgende Koordinaten:
$M^{'} (\frac{34}{9} | \frac{34}{9} | \frac{35}{9})$
Bestimmung des Radius des Schnittkreises
Den Radius des Schnittkreises berechnest du mit Hilfe des Satzes von Pythagoras. (Anmerkung: In der Abbildung wird der Radius $r_{1}^{'}$ mit $r^{'}$ bezeichnet.)
$\begin{array}{rcl} r_{1}^{'} & = & \sqrt{r^{2} - d^{2}} \\ = & \sqrt{(7^{2} - (\frac{19}{3})^{2})} \\ = & \sqrt{\frac{80}{9}} \\ \approx & 2,98 \end{array}$
Antwort: Der Radius des Schnittkreises beträgt etwa 2,98.
Zusätzliche Zeichnung zur Veranschaulichung
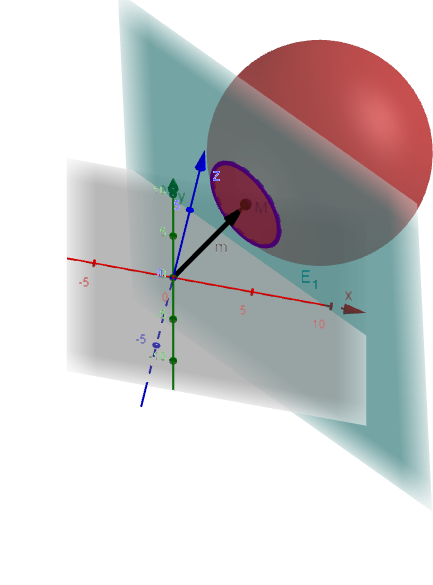
Teilaufgabe 2
Setze die Koordinaten von $P$ in die Kugelgleichung ein und berechne $z$ .
Die Kugel $K$ mit dem Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ und dem Radius $r$ hat folgende Gleichung:
$K : (x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}$
Setze die Koordinaten von $M (8 | 8 | 6)$ und den Radius $r = 7$ ein:
$K : (x_{1} - 8)^{2} + (x_{2} - 8)^{2} + (x_{3} - 6)^{2} = 7^{2} = 49$
Wenn der Punkt $P (6 | z | 2)$ auf der Kugeloberfläche liegen soll, müssen seine Koordinaten die Kugelgleichung erfüllen. Setze die Koordinaten ein und löse nach $z$ auf.
$\begin{array}{rcl} (6 - 8)^{2} + (z - 8)^{2} + (2 - 6)^{2} & = & 49 \\ 4 + (z - 8)^{2} + 16 & = & 49 \\ (z - 8)^{2} & = & 29 \\ z_{1 / 2} & = & 8 \pm \sqrt{29} \end{array}$
Da aber $z > 8$ sein soll, gibt es nur die Lösung $z = 8 + \sqrt{29}$ .
Antwort: Der Punkt $P$ mit den Koordinaten $(6 | 8 + \sqrt{29} | 2)$ liegt auf der Kugeloberfläche.
Teilaufgabe 3
Die Gleichung für eine Tangentialebene $T$ im Punkt $P$ der Kugel $K$ mit dem Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ lautet:
$T : (\vec{x} - \vec{p}) \circ (\vec{p} - \vec{m}) = 0$
Setze $P$ und $M$ in $T$ ein:
$\begin{array}{rrccl} T : & (\vec{x} - (\begin{array}{c} 6 \\ 8 + \sqrt{29} \\ 2 \end{array})) & \circ ((\begin{array}{c} 6 \\ 8 + \sqrt{29} \\ 2 \end{array}) - (\begin{array}{c} 8 \\ 8 \\ 6 \end{array})) & = & 0 \\ (\vec{x} - (\begin{array}{c} 6 \\ 8 + \sqrt{29} \\ 2 \end{array})) & \circ (\begin{array}{c} - 2 \\ \sqrt{29} \\ - 4 \end{array}) & = & 0 \end{array}$
Das Skalarprodukt wird mit Hilfe des Distributivgesetzes ausmultipliziert:
$\begin{array}{rccl} - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - (6 \cdot (- 2) + (8 + \sqrt{29}) \cdot \sqrt{29} + 2 \cdot (- 4)) & = & 0 \\ - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - (- 12 + 8 \cdot \sqrt{29} + 29 - 8) & = & 0 \\ - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - (9 + 8 \cdot \sqrt{29}) & = & 0 \\ - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} & = & (9 + 8 \cdot \sqrt{29}) \end{array}$
$T : - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} = (9 + 8 \cdot \sqrt{29})$
Antwort: Die obige Gleichung $T$ ist die Gleichung der Tangentialebene in Koordinatenform, die die Kugel $K$ im Punkt $P$ berührt.
Teilaufgabe 4
Eine zu T parallele Ebene hat den gleichen Normalenvektor wie die Ebene $T$ . Die rechte Seite der Ebenengleichung ist allerdings verschieden.
Eine zu $T$ parallele Ebene $T_{1}$ hat somit folgende Gleichung:
$T_{1} : - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} = a$
Die Unbekannte $a$ kannst du über die Bedingung, dass der Schnittkreisradius $r_{2}^{'} = 3$ sein soll, bestimmen.
Wiederum gilt der Satz von Pythagoras: $r_{2}^{' 2} = r^{2} - d^{2} \Rightarrow d^{2} = r^{2} - r_{2}^{' 2}$ .
Mit $r_{2}^{'} = 3$ und $r = 7$ folgt: $d^{2} = 7^{2} - 3^{2} = 40 \Rightarrow d = \pm \sqrt{40}$
Da der Abstand positiv sein soll gilt: $d = \sqrt{40}$ .
Die Tangentialebene $T_{1}$ muss also den Abstand $d_{T_{1}} = \sqrt{40}$ vom Kugelmittelpunkt haben.
Erstelle von $T_{1}$ die Hessesche Normalenform:
$\begin{array}{rrcl} H N F_{T_{1}} : & \frac{- 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - a}{\sqrt{(- 2)^{2} + (\sqrt{29})^{2} + (- 4)^{2}}} & = & 0 \\ \frac{- 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - a}{\sqrt{4 + 29 + 16}} & = & 0 \\ \frac{- 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - a}{\sqrt{49}} & = & 0 \\ \frac{- 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} - a}{7} & = & 0 \end{array}$
Setze nun die Koordinaten des Kugelmittelpunktes in die $H N F$ von $T_{1}$ ein und verlange, dass der Abstand $d_{T_{1}} = \sqrt{40}$ sein soll.
$\begin{array}{rcll} d_{T_{1}} & = & | \frac{- 2 \cdot 8 + \sqrt{29} \cdot 8 - 4 \cdot 6 - a}{7} | \\ \sqrt{40} & = & | \frac{- 2 \cdot 8 + \sqrt{29} \cdot 8 - 4 \cdot 6 - a}{7} | \\ \sqrt{40} & = & | \frac{- 16 + \sqrt{29} \cdot 8 - 24 - a}{7} | \\ \sqrt{40} & = & | \frac{\sqrt{29} \cdot 8 - 40 - a}{7} | & | \cdot 7 \\ 7 \cdot \sqrt{40} & = & | 8 \cdot \sqrt{29} - 40 - a | \end{array}$
Führe nun eine Fallunterscheidung durch:
$I : 8 \cdot \sqrt{29} - 40 - a > 0$
$II : 8 \cdot \sqrt{29} - 40 - a < 0$
Aus $I$ folgt:
$\begin{array}{rrcl} 7 \cdot \sqrt{40} & = & 8 \cdot \sqrt{29} - 40 - a \\ \Rightarrow & a_{1} & = & 8 \cdot \sqrt{29} - 7 \cdot \sqrt{40} - 40 \end{array}$
Aus $II$ folgt:
$\begin{array}{rcl} 7 \cdot \sqrt{40} & = & - (8 \cdot \sqrt{29} - 40 - a) = - 8 \cdot \sqrt{29} + 40 + a \\ \Rightarrow & a_{2} & = & 8 \cdot \sqrt{29} + 7 \cdot \sqrt{40} - 40 \end{array}$
Somit hast du zwei Lösungen gefunden.
Antwort: Es gibt zwei Ebenen die zu $T$ parallel sind und deren Schnittkreisradius mit der Kugel $r_{2}^{'} = 3$ beträgt.
$T_{1} : - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} = 8 \cdot \sqrt{29} - 7 \cdot \sqrt{40} - 40$
$T_{2} : - 2 x_{1} + \sqrt{29} x_{2} - 4 x_{3} = 8 \cdot \sqrt{29} + 7 \cdot \sqrt{40} - 40$
Zusätzliche Visualisierung
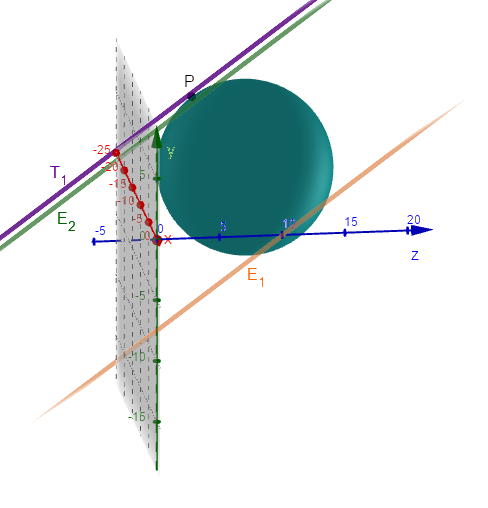
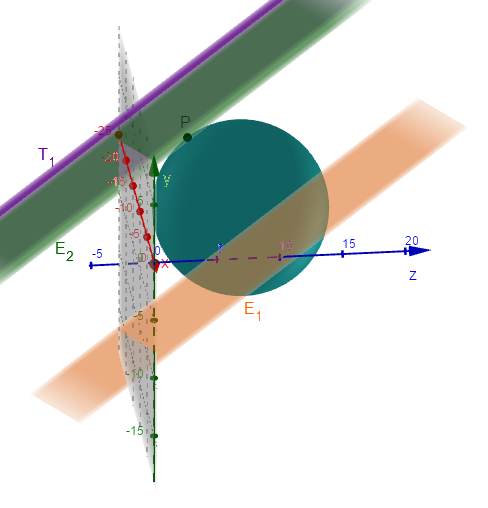
Du kannst die Aufgabe mit folgender Strategie lösen:
Strategie zu Teilaufgabe 1
Berechne den Abstand des Kugelmittelpunktes von der Ebene $E$ . Dazu benötigst du die Hessesche Normalenform. Wandle dazu die Parameterform der Ebene $E$ in eine Koordinatenform um. Aus der Koordinatenform erhältst du die Hessesche Normalenform. Setze den Kugelmittelpunkt in die Hessesche Normalenform ein und du erhältst den Abstand $d$ des Kugelmittelpunktes von der Ebene $E$ . Hier kannst du dann drei Fälle unterscheiden; die Ebene schneidet die Kugel, die Ebene berührt die Kugel oder es gibt keine gemeinsamen Punkte zwischen der Kugel und der Ebene.
Den Mittelpunkt $M^{'}$ des Schnittkreises berechnest du indem du die Lotgerade von $M$ auf die Ebene $E$ mit der Ebene $E$ schneidest.
Den Radius des Schnittkreises berechnest du mit Hilfe des Satzes von Pythagoras.
Strategie zu Teilaufgabe 2
Setze die Koordinaten von $P$ in die Kugelgleichung ein und berechne $z$ . Beachte, dass $z > 8$ sein soll.
Strategie zu Teilaufgabe 3
Setze den berechneten Punkt $P$ in die Tangentialebenengleichung ein.
Strategie zu Teilaufgabe 4
Stelle die Gleichung einer zu $T$ parallelen Ebene $T_{1}$ mit unbekannter rechten Seite auf. Der Radius $r_{2}^{'}$ des Schnittkreises soll $3$ betragen. Das liefert die Bedingung für den Abstand $d_{T_{1}}$ des Kugelmittelpunktes zu $T_{1}$ . Aus dem berechneten Abstand und der $H N F$ der Ebene $T_{1}$ kannst du die unbekannte rechte Seite der parallelen Ebene berechnen.
2
Gegeben ist die Kugel K mit der Gleichung $K : [\vec{x} - (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array})] \circ [\vec{x} - (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array})] = 36$ und die Ebene $E_{1} : 4 x_{1} + 4 x_{2} + 2 x_{3} = - 22$ .
1) Zeige, dass $E_{1}$ Tangentialebene an $K$ ist und berechne den Berührpunkt $B$ .
2) Durch $F_{a} : 2 \cdot x_{1} + 4 \cdot x_{2} + 6 \cdot x_{3} = a$ wird eine Ebenenschar bestimmt. Berechne für welche Parameterwerte die Kugel $K$ und die Ebene $F_{a}$
gemeinsame Punkte haben. Bestimme für welche Werte von $a$ ein Schnittkreis mit Radius $r = 2,2$ entsteht und berechne die zugehörigen Kreismittelpunkte.
3) Der Punkt $A (8 | 2 | - 1)$ liegt auf $K$ . Stelle die Gleichung der Tangentialebene $E_{2}$ in $A$ in Koordinatenform auf.
4) Die Ebenen $E_{1}$ und $E_{2}$ bilden eine Rinne für die Kugel $K$ , in der diese entlang rollt. Gib eine Gleichung der Geraden $g$ an, auf der sich der Mittelpunkt $M$ der Kugel bewegt.
5) Die Ebene $E_{3} : 2 x_{2} - 4 x_{3} = - 96$ steht senkrecht zu $E_{1}$ und $E_{2}$ . Berechne die Länge der Strecke die die Kugel $K$ vom Startpunkt aus zurücklegt, bis diese von $E_{3}$ gestoppt wird.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis und Kugel
Teilaufgabe 1
Bestimmung der Art des Schnitts von Ebene und Kugel
Um die hessesche Normalenform einer Ebene zu berechnen, teilt man die Ebenengleichung in Koordinatenform durch den Betrag des Normalenvektors $| \vec{n} |$ . Wenn die Koordinatengleichung der Ebene gegeben ist, kann der Normalenvektor aus der Koordinatengleichung der Ebene abgelesen werden. Die Koeffizienten in der Ebenengleichung ergeben den Normalenvektor.
$\vec{n} = (\begin{array}{c} 4 \\ 4 \\ 2 \end{array}) \Rightarrow | \vec{n} | = \sqrt{4^{2} + 4^{2} + 2^{2}} = \sqrt{36} = 6$
$H N F : \frac{4 x_{1} + 4 x_{2} + 2 x_{3} + 22}{6} = 0$
Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein:
$\begin{array}{rcl} d (M, E) & = & | \frac{4 \cdot 2 + 4 \cdot 2 + 2 \cdot (- 1) + 22}{6} | \\ = & | \frac{36}{6} | \\ = & 6 \end{array}$
Der Abstand des Kugelmittelpunktes von der Ebene $E_{1}$ beträgt $6$ und ist somit gleich dem Kugelradius $r = 6.$
Antwort: Die Ebene $E_{1}$ ist eine Tangentialebene.
Berechnung des Berührpunktes $B$
Stelle die Gleichung der Lotgeraden von $M$ auf die Ebene $E_{1}$ auf, indem Du für den Stützvektor den Vektor zum Kugelmittelpunkt und als Richtungsvektor den Normalenvektor $\vec{n}$ der Ebene $E_{1}$ verwendest.
$g_{L o t} : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + t \cdot (\begin{array}{c} 4 \\ 4 \\ 2 \end{array})$
Schneide $g_{L o t}$ mit der Ebene $E_{1}$ :
$\begin{array}{rcl} 4 \cdot (2 + 4 t) + 4 \cdot (2 + 4 t) + 2 \cdot (- 1 + 2 t) + 22 & = & 0 \\ 8 + 16 t + 8 + 16 t - 2 + 4 t + 22 & = & 0 \\ 36 t & = & - 36 \\ t & = & - 1 \end{array}$
Setze $t = - 1$ in die Geradengleichung ein und Du erhältst den Vektor zum Berührpunkt $B$ .
$\begin{array}{l} \vec{x_{B}} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + (- 1) \cdot (\begin{array}{c} 4 \\ 4 \\ 2 \end{array}) = (\begin{array}{c} - 2 \\ - 2 \\ - 3 \end{array}) \\ \Rightarrow B (- 2 | - 2 | - 3) \end{array}$
Antwort: Der Berührpunkt $B$ zwischen der Kugel und der Ebene $E_{1}$ hat folgende Koordinaten:
$B (- 2 | - 2 | - 3)$
Die nebenstehende Abb. ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.
Dargestellt sind die Kugel $K$ , die Ebene $E_{1}$ und der Berührpunkt $B$ .
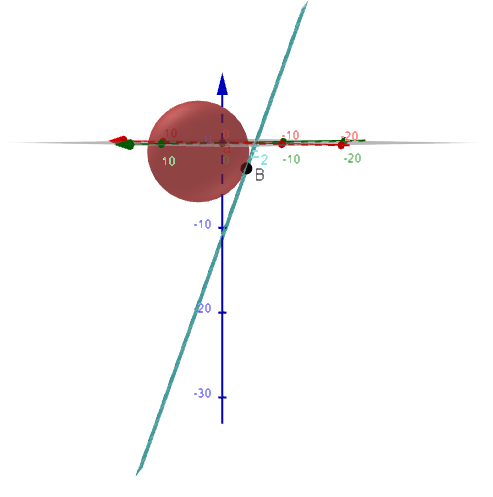
Teilaufgabe 2
Bestimmung der hessischen Normalenform der Ebenenschar $F_{a}$
Berechne zunächst den Normalenvektor der Ebenenschar:
$\vec{n} = (\begin{array}{c} 2 \\ 4 \\ 6 \end{array}) \Rightarrow | \vec{n} | = \sqrt{2^{2} + 4^{2} + 6^{2}} = \sqrt{56}$
Die Ebenengleichung $F_{a}$ in Koordinatenform wird durch den Betrag des Normalenvektors $| \vec{n} |$ geteilt und Du erhältst die hessesche Normalenform.
$H N F : \frac{2 x_{1} + 4 x_{2} + 6 x_{3} - a}{\sqrt{56}} = 0$
Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein und verlange, dass der berechnete Abstand kleiner als der Kugelradius ist :
$\begin{aligned} d (M, F_{a}) = | \frac{2 \cdot 2 + 4 \cdot 2 + 6 \cdot (- 1) - a}{\sqrt{56}} | < & 6 \\ | \frac{6 - a}{\sqrt{56}} | < & 6 | \cdot \sqrt{56} \\ | 6 - a | < & 6 \cdot \sqrt{56} \end{aligned}$
Führe nun eine Fallunterscheidung durch:
$\begin{array}{cccccccl} 6 - a > & 0 & | & I \\ 6 - a < & 0 & | & II \end{array}$
Aus $I$ folgt:
$6 - a < 6 \cdot \sqrt{56} \Rightarrow a > 6 - 6 \cdot \sqrt{56} \approx - 38,9$
Aus $II$ folgt:
$- (6 - a) < 6 \cdot \sqrt{56} \Rightarrow - 6 + a < 6 \cdot \sqrt{56} \Rightarrow a < 6 + 6 \cdot \sqrt{56} \approx 50,9$
Antwort: Wenn der Parameter $a$ größer als $6 - 6 \cdot \sqrt{56}$ oder kleiner als $6 + 6 \cdot \sqrt{56}$ ist, haben die Ebene $F_{a}$ und die Kugel $K$ gemeinsame Punkte, d.h. es gibt einen Schnittkreis.
Bestimmung des Parameter $a$ , so dass der Schnittkreisradius $r = 2,2$ beträgt
Den Abstand $d$ des Mittelpunktes $M^{'}$ vom Mittelpunkt $M$ berechnest Du mit Hilfe des Satzes von Pythagoras.
$\begin{array}{rcl} d & = & \sqrt{r^{2} - {r^{'}}^{2}} \\ = & \sqrt{6^{2} - {2,2}^{2}} \\ = & \sqrt{31,16} \\ \approx & 5,58 \end{array}$
Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein.
(Diesen Rechenschritt hast Du schon zu Beginn der Teilaufgabe 2 gelöst.)
Verlange, dass der berechnete Abstand gleich $\sqrt{31,16}$ ist. Du erhältst folgende Gleichung:
$\begin{aligned} \sqrt{31,16} & = | \frac{6 - a}{\sqrt{56}} | | \cdot \sqrt{56} \\ \sqrt{31,16} \cdot \sqrt{56} & = | 6 - a | \\ \sqrt{1744,96} & = | 6 - a | \end{aligned}$
Führe nun eine Fallunterscheidung durch:
$\begin{array}{cccccccl} 6 - a > & 0 & | & I \\ 6 - a < & 0 & | & II \end{array}$
Aus $I$ folgt:
$6 - a = \sqrt{1744,96} \Rightarrow a = 6 - \sqrt{1744,96} \approx - 35,77$
Aus $II$ folgt:
$- (6 - a) = \sqrt{1744,96} \Rightarrow - 6 + a = \sqrt{1744,96} \Rightarrow$
$a = 6 + \sqrt{1744,96} \approx 47,77$
Antwort: Du hast zwei Parameter erhalten. Für $a = 6 - \sqrt{1744,96}$ bzw. $a = 6 + \sqrt{1744,96}$ haben die Ebenen $F_{a}$ einen Schnittkreisradius von $r = 2,2$ .
Bestimmung des Mittelpunktes $M^{'}$ des Schnittkreises
Du berechnest die Lotgerade von $M$ auf die Ebene $F_{a}$ . Dazu verwendest Du den Vektor zum Kugelmittelpunkt als Stützvektor und als Richtungsvektor nimmst Du den Normalenvektor $\vec{n}$ der Ebene $F_{a}$ .
$g_{L o t} : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + t \cdot (\begin{array}{c} 2 \\ 4 \\ 6 \end{array})$
Schneide $g_{L o t}$ mit der Ebene $F_{a}$ :
$\begin{array}{rcl} 2 \cdot (2 + 2 t) + 4 \cdot (2 + 4 t) + 6 \cdot (- 1 + 6 t) - a & = & 0 \\ 4 + 4 t + 8 + 16 t - 6 + 36 t - a & = & 0 \\ 56 t + 6 - a & = & 0 \\ t & = & \frac{a - 6}{56} \end{array}$
Für $a$ gibt es zwei Werte, so dass sich zwei Parameterwerte für $t$ ergeben:
$\begin{array}{l} t_{1} = \frac{6 - \sqrt{1744,96} - 6}{56} = - \frac{\sqrt{1744,96}}{56} \approx - 0,746 \\ t_{2} = \frac{6 + \sqrt{1744,96} - 6}{56} = \frac{\sqrt{1744,96}}{56} \approx 0,746 \end{array}$
Setze $t_{1}$ in die Geradengleichung ein und Du erhältst den Vektor zum Schnittkreismittelpunkt $M_{1}^{'}$ :
$\begin{array}{l} \vec{x_{M_{1}^{'}}} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) - \frac{\sqrt{1744,96}}{56} \cdot (\begin{array}{c} 2 \\ 4 \\ 6 \end{array}) \approx (\begin{array}{c} 0,5081 \\ - 0,9838 \\ - 5,4756 \end{array}) \\ \Rightarrow M_{1}^{'} (0,5081 | - 0,9838 | - 5,4756) \end{array}$
Setze $t_{2}$ in die Geradengleichung ein und Du erhältst den Vektor zum Schnittkreismittelpunkt $M_{2}^{'}$ :
$\begin{array}{l} \vec{x_{M_{2}^{'}}} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + \frac{\sqrt{1744,96}}{56} \cdot (\begin{array}{c} 2 \\ 4 \\ 6 \end{array}) \approx (\begin{array}{c} 3,4919 \\ 4,9838 \\ 3,4756 \end{array}) \\ \Rightarrow M_{2}^{'} (3,4919 | 4,9838 | 3,4756) \end{array}$
Antwort: Für die Schnittkreismittelpunkte ergeben sich die gerundeten Koordinaten $M_{1}^{'} (0,5081 | - 0,9838 | - 5,4756)$ und $M_{2}^{'} (3,4919 | 4,9838 | 3,4756)$ .
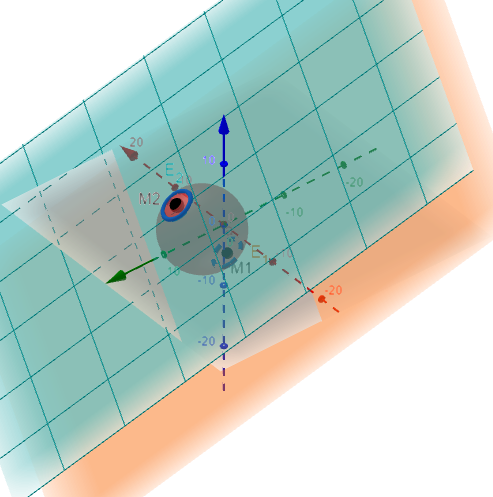
Die nebenstehende Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.
Dargestellt sind die Kugel $K$ , die Ebenen $F_{47,77}$ (türkisfarbig), $F_{- 35,77}$ (orangefarbig) und die Schnittkreismittelpunkte $M_{1}^{'}$ bzw. $M_{2}^{'}$ .
(Der deutlich sichtbare Punkt ist $M_{2}^{'}$ .)
Teilaufgabe 3
Berechnung der Tangentialebenengleichung $E_{2}$
Die Gleichung für eine Tangentialebene $E_{2}$ im Punkt $A$ der Kugel $K$ mit dem Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ lautet:
$E_{2} : (\vec{x} - \vec{a}) \circ (\vec{a} - \vec{m}) = 0$
Setze $A$ und $M$ in $E_{2}$ ein:
$\begin{array}{rrccl} E_{2} : & (\vec{x} - (\begin{array}{c} 8 \\ 2 \\ - 1 \end{array})) & \circ ((\begin{array}{c} 8 \\ 2 \\ - 1 \end{array}) - (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array})) & = & 0 \\ (\vec{x} - (\begin{array}{c} 8 \\ 2 \\ - 1 \end{array})) & \circ (\begin{array}{c} 6 \\ 0 \\ 0 \end{array}) & = & 0 \end{array}$
Das Skalarprodukt wird mit Hilfe des Distributivgesetzes ausmultipliziert:
$\begin{array}{rcl} 6 x_{1} + 0 x_{2} + 0 x_{3} - (8 \cdot 6 + 2 \cdot 0 + (- 1) \cdot 0) & = & 0 \\ 6 x_{1} + 0 x_{2} + 0 x_{3} - (48 + 0 + 0) & = & 0 \\ 6 x_{1} - 48 & = & 0 \\ x_{1} & = & 8 \end{array}$
Antwort: Die Gleichung für die Tangentialebene $E_{2}$ im Punkt $A$ der Kugel $K$ lautet: $x_{1} = 8$
Teilaufgabe 4
Berechnung der Schnittgeraden der Ebenen $E_{1}$ und $E_{2}$
$\begin{array}{cccccccl} E_{1} : 4 x_{1} & + & 4 x_{2} & + & 2 x_{3} & = & - 22 & und \\ E_{2} : x_{1} & = & 8 \end{array}$
Hier bietet sich das Einsetzungsverfahren an. Setze $x_{1} = 8$ in $E_{1}$ ein und löse nach $x_{2}$ auf:
$\begin{array}{rcl} 4 \cdot 8 + 4 x_{2} + 2 x_{3} & = & - 22 \\ 32 + 4 x_{2} + 2 x_{3} & = & - 22 \\ 4 x_{2} + 2 x_{3} & = & - 54 \\ x_{2} & = & - 13,5 - 0,5 x_{3} \end{array}$
Du hast nun $x_{2}$ in Abhängigkeit von $x_{3}$ dargestellt. Für $x_{3}$ kannst Du z. B. den Parameter $t$ setzen. Somit hat die Lösungsmenge des Gleichungssystems folgende Form:
$𝕃 = {(8 | - 13,5 - 0,5 t | t) | t \in ℝ}$
Mit Vektoren geschrieben sieht die Lösungsmenge folgendermaßen aus:
$\vec{x} = (\begin{array}{c} 8 \\ - 13,5 - 0,5 t \\ t \end{array}) = (\begin{array}{c} 8 \\ - 13,5 \\ 0 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 0,5 \\ 1 \end{array})$
Die Schnittgerade der beiden Ebenen lautet somit:
$g (E_{1}, E_{2}) : \vec{x} = (\begin{array}{c} 8 \\ - 13,5 \\ 0 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 0,5 \\ 1 \end{array})$
Erstelle nun die Geradengleichung $g$ auf der sich der Kugelmittelpunkt bewegt. Dazu liefert Dir die Geradengleichung $g (E_{1}, E_{2})$ den Richtungsvektor der Geraden $g$ . Der Stützvektor der Geraden $g$ ist der Vektor zum Kugelmittelpunkt.
Antwort: Die Gleichung der Geraden $g$ auf der sich der Kugelmittelpunkt bewegt lautet:
$g : \vec{x} = (\begin{array}{c} 2 \\ 2 \\ - 1 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 0,5 \\ 1 \end{array})$
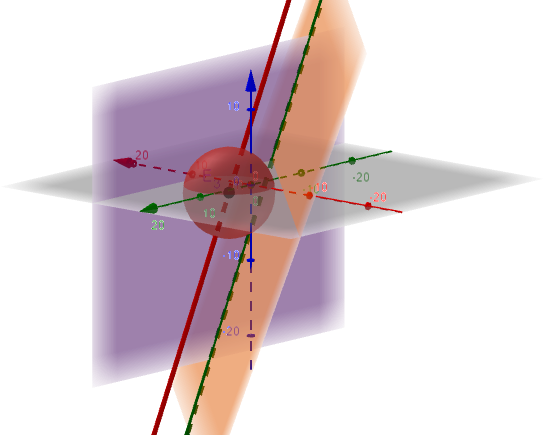
Die nebenstehende Abb. ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.
Dargestellt sind die Kugel $K$ , die Ebenen $E_{1}$ und $E_{2}$ , die Schnittgerade der beiden Ebenen (in grün) und die Gerade g auf der sich der Kugelmittelpunkt bewegt (in rot).
Teilaufgabe 5
Berechnung der Länge der Strecke, die die Kugel vom Startpunkt aus zurücklegt
Die nebenstehende Skizze zeigt Dir wie Du den zurückgelegten Weg berechnen kannst. Du berechnest den Abstand $d (M, E_{3})$ des Kugelmittelpunktes von der Ebene $E_{3}$ . Den zurückgelegten Weg $s$ findest Du als Differenz von $d (M, E_{3})$ und dem Kugelradius $r$ .
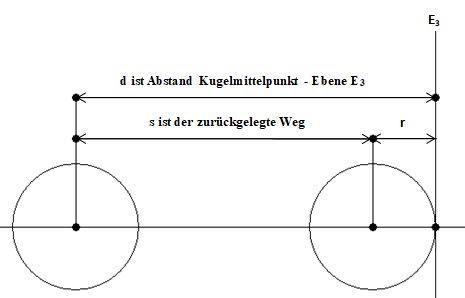
Für die Abstandsberechnung benötigst Du wieder die hessesche Normalenform der Ebene $E_{3}$ .
Der Normalenvektor der Ebene $E_{3}$ lautet:
$\vec{n} = (\begin{array}{c} 0 \\ 2 \\ - 4 \end{array}) \Rightarrow | \vec{n} | = \sqrt{0^{2} + 2^{2} + (- 4)^{2}} = \sqrt{20}$
Die Ebenengleichung $E_{3}$ in Koordinatenform wird durch den Betrag des Normalenvektors $| \vec{n} |$ geteilt und Du erhältst die hessesche Normalenform.
$H N F : \frac{2 x_{2} - 4 x_{3} + 96}{\sqrt{20}} = 0$
Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein:
$\begin{array}{rcl} d (M, E_{3}) & = & | \frac{2 \cdot 2 - 4 \cdot (- 1) + 96}{\sqrt{20}} | \\ = & | \frac{104}{\sqrt{20}} | \\ = & 5,2 \cdot \sqrt{20} \end{array}$
Für den zurückgelegten Weg gilt:
$s = d (M, E_{3}) - r \Rightarrow s = 5,2 \cdot \sqrt{20} - 6 \approx 17,26$
Antwort: Die Länge der Strecke $s$ , die die Kugel $K$ vom Startpunkt aus zurückgelegt hat, beträgt etwa 17,26.
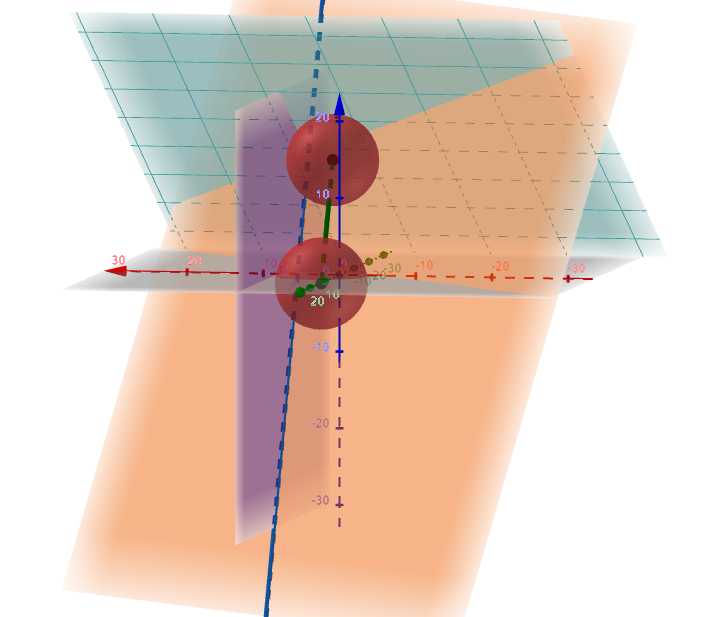
Die nebenstehende Abb. ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung des Sachverhaltes.
Dargestellt sind die Kugel $K$ am Startpunkt und am Ende der zurückgelegten Strecke (in grün) , die Ebenen $E_{1}$ (orange), $E_{2}$ (lila) und $E_{3}$ (türkis) und die Schnittgerade (blau) der beiden Ebenen $E_{1}$ und $E_{2}$ .
Du kannst die Aufgabe mit folgender Strategie lösen:
Strategie zu Teilaufgabe 1
Berechne den Abstand des Kugelmittelpunktes von der Ebene $E_{1}$ . Dazu benötigst Du die hessesche Normalenform die Du aus der Koordinatenform der Ebene $E_{1}$ berechnen kannst. Setze den Kugelmittelpunkt $M$ in die hessesche Normalenform ein und Du erhältst den Abstand $d$ des Kugelmittelpunktes von der Ebene $E_{1}$ . Da $E_{1}$ Tangentialebene sein soll, muss der Abstand $d$ gleich dem Kugelradius $r = 6$ sein. Den Berührpunkt $B$ berechnest Du, indem Du die Lotgerade von $M$ auf die Ebene $E_{1}$ mit der Ebene $E_{1}$ schneidest.
Strategie zu Teilaufgabe 2
Du benötigst die hessesche Normalenform der Ebene $F_{a}$ . Berechne dann den Abstand des Kugelmittelpunktes $M$ von der Ebene $F_{a}$ . Um einen Schnittkreis zu erhalten muss dieser Abstand $d (M, F_{a})$ kleiner als der Kugelradius $r = 6$ sein.
Der Radius $r^{'}$ des Schnittkreises soll $2,2$ betragen. Der Satz von Pythagoras liefert die Bedingung für den Abstand $d$ des Kugelmittelpunktes zu $F_{a}$ . In die $H N F$ der Ebene $F_{a}$ setzt Du nun die Koordinaten des Kugelmittelpunktes ein und verlangst, dass der berechnete Abstand gleich dem Abstand $d$ ist. Nun kannst Du den Parameter $a$ berechnen.
Den Mittelpunkt $M^{'}$ des Schnittkreises berechnest Du indem Du die Lotgerade von $M$ auf die Ebene $F_{a}$ mit der Ebene $F_{a}$ schneidest. Beachte dabei, dass Du die beiden vorher erhaltenen Werte für den Parameter $a$ benutzt um zwei Schnittkreismittelpunkte zu berechnen.
Strategie zu Teilaufgabe 3
Setze den gegebenen Punkt $A$ in die Tangentialebenengleichung ein und Du erhältst die Ebenengleichung $E_{2}$ .
Strategie zu Teilaufgabe 4
Schneide die Ebenen $E_{1}$ und $E_{2}$ um die Schnittgerade zu berechnen. Für die Gleichung der Geraden $g$ auf der sich der Kugelmittelpunkt bewegt wählst Du als Stützvektor den Vektor zum Kugelmittelpunkt und als Richtungsvektor den Richtungsvektor der Schnittgeraden von $E_{1}$ und $E_{2}$ .
Strategie zu Teilaufgabe 5
Du benötigst die hessesche Normalenform der Ebene $E_{3}$ . Berechne dann den Abstand $d (M, E_{3})$ des Kugelmittelpunktes $M$ von der Ebene $E_{3}$ . Du berechnest die Länge der Strecke $s$ , die die Kugel $K$ vom Startpunkt aus zurückgelegt hat, als Differenz von $d (M, E_{3})$ und dem Kugelradius $r$ .
3
Untersuche, welche Lage die Ebene $E$ zur Kugel $K$ hat. Berechne dazu den Abstand des Kugelmittelpunktes $M$ von der Ebene $E$ .
$E : 3 x_{1} + 4 x_{2} + 5 x_{3} = 2; M (2 | 1 | 3); r = 3$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Hessesche Normalenform
Wandle die Ebene E in die Hessesche Normalenform um:
$E_{H N F} : \frac{3 x_{1} + 4 x_{2} + 5 x_{3} - 2}{\sqrt{3^{2} + 4^{2} + 5^{2}}} = 0$
Setze die Koordinaten des Kugelmittelpunktes ein:
$d (M, E) = | \frac{3 \cdot 2 + 4 \cdot 1 + 5 \cdot 3 - 2}{\sqrt{3^{2} + 4^{2} + 5^{2}}} | = | \frac{23}{\sqrt{50}} | \approx 3,25 > 3$
Antwort: Der Abstand $d \approx 3,25$ des Kugelmittelpunktes $M$ von der Ebene $E$ ist größer als der Kugelradius $r = 3$ , d.h. die Ebene schneidet die Kugel nicht.
4
Zeige, dass die Ebene $E : 3 x_{1} + x_{2} - 2 x_{3} = 16$ eine Tangentialebene an die Kugel $K$ mit dem Mittelpunkt $M (4 | 0 | 5)$ und dem Radius $r = \sqrt{14}$ ist. Berechne auch den Berührpunkt $B$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentialebene
Stelle die Hessesche Normalenform der Ebene $E$ auf.
$E_{H N F} : \frac{3 x_{1} + x_{2} - 2 x_{3} - 16}{\sqrt{3^{2} + 1^{2} + (- 2)^{2}}}$ $=$ $0$
↓
Berechne die Wurzel.
$E_{H N F} : \frac{3 x_{1} + x_{2} - 2 x_{3} - 16}{\sqrt{14}}$ $=$ $0$
Berechne den Abstand des Mittelpunktes $M (4 | 0 | 5)$ von der Ebene $E$ , indem du die Koordinaten von $M$ in die Hessesche Normalenform einsetzt.
$d (M, E)$ $=$ $| \frac{3 \cdot 4 + 0 - 2 \cdot 5 - 16}{\sqrt{14}} |$
↓
vereinfache
$=$ $| \frac{- 14}{\sqrt{14}} |$
↓
Berechne den Betrag.
$=$ $\frac{14}{\sqrt{14}}$
↓
Vereinfache weiter, indem du $14$ durch $\sqrt{14} \cdot \sqrt{14}$ ersetzt.
$=$ $\frac{\sqrt{14} \cdot \sqrt{14}}{\sqrt{14}}$
↓
Kürze den Bruch.
$=$ $\sqrt{14}$
Der Abstand des Mittelpunktes $M$ von der Ebene $E$ ist $d = \sqrt{14}$ . Der Kugelradius ist $r = \sqrt{14}$ . Da $d = r$ ist, handelt es sich um eine Tangentialebene.
Berechnung des Berührpunktes:
Stelle die Gleichung der Lotgeraden $g_{L o t}$ durch den Mittelpunkt auf die Ebene $E$ auf. Verwende als Aufpunkt den Mittelpunkt $M$ und als Richtungsvektor den Normalenvektor der Ebene $E$ .
$g_{L o t} : \vec{X} = (\begin{array}{c} 4 \\ 0 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 3 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4 + 3 t \\ t \\ 5 - 2 t \end{array})$
Berechne den Berührpunkt, indem du die Lotgerade $g_{L o t}$ mit der Ebene $E$ schneidest: $g_{L o t} \cap E$
$E : 3 x_{1} + x_{2} - 2 x_{3}$ $=$ $16$
↓
Setze $g$ in $E$ ein.
$3 \cdot (4 + 3 t) + t - 2 \cdot (5 - 2 t)$ $=$ $16$
↓
Löse die Klammern auf.
$12 + 9 t + t - 10 + 4 t$ $=$ $16$
↓
Vereinfache die linke Seite.
$14 t + 2$ $=$ $16$ $- 2$
↓
Löse nach $t$ auf.
$14 t$ $=$ $14$ $: 14$
$t$ $=$ $1$
Zur Berechnung des Berührpunktes setzt du $t = 1$ in die Gleichung der Lotgeraden ein.
${\vec{X}}_{B} = (\begin{array}{c} 4 \\ 0 \\ 5 \end{array}) + 1 \cdot (\begin{array}{c} 3 \\ 1 \\ - 2 \end{array}) = (\begin{array}{c} 4 + 3 \\ 0 + 1 \\ 5 - 2 \end{array}) = (\begin{array}{c} 7 \\ 1 \\ 3 \end{array})$
Antwort: Der Berührpunkt hat die Koordinaten $B (7 | 1 | 3)$ .
Berechne den Abstand $d$ des Kugelmittelpunktes $M$ von der Ebene $E$ . Stelle dazu die Hessesche Normalenform der Ebene $E$ auf. Ist der berechnete Abstand $d$ gleich dem Kugelradius $r$ , dann ist $E$ eine Tangentialebene.
Für die Berechnung des Berührpunktes benötigst du die Gleichung der Lotgeraden durch den Punkt $M$ auf die Ebene $E$ . Verwende als Aufpunkt den Mittelpunkt $M$ und als Richtungsvektor den Normalenvektor der Ebene $E$ . Schneide die Lotgerade mit der Ebene $E$ .
5
Eine Kugel $K$ hat den Mittelpunkt $M$ und den Radius $r = 4$ . Der Kugelmittelpunkt liegt auf einer Geraden mit der Gleichung $g : \vec{X} = (\begin{array}{c} 2 \\ 6 \\ 1 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 4 \\ 0 \end{array})$ . Die Ebene $E : x_{2} = 6$ berührt die Kugel $K$ .
Bestimme die Koordinaten eines möglichen Mittelpunktes $M$ der Kugel.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kugel und Geraden
Der Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ liegt auf der Geraden $g$ . Setze ein.
$(\begin{array}{c} m_{1} \\ m_{2} \\ m_{3} \end{array}) = (\begin{array}{c} 2 \\ 6 \\ 1 \end{array}) + t \cdot (\begin{array}{c} 0 \\ - 4 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 6 - 4 t \\ 1 \end{array})$
Erstelle von der Ebene $E : x_{2} = 6$ die Hessesche Normalenform:
Allgemein gilt: $E_{H N F} : \frac{a \cdot x_{1} + b \cdot x_{2} + c \cdot x_{3} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0$
$E_{H N F} : \frac{0 \cdot x_{1} + 1 \cdot x_{2} + 0 \cdot x_{3} - 6}{\sqrt{0^{2} + 1^{2} + 0^{2}}} = x_{2} - 6 = 0$
Der Abstand des Punktes $M$ von der Ebene $E$ soll gleich dem Kugelradius $r = 4$ sein.
$d (M, E) = | 6 - 4 t - 6 | = | - 4 t | = 4$
Löse den Betrag auf:
Fall -
$4 t = 4 \Rightarrow t_{1} = 1$
Fall +
$- 4 t = 4 \Rightarrow t_{2} = - 1$
Du hast zwei Lösungen für den Parameter $t$ erhalten. Demzufolge gibt es auch zwei Kugelmittelpunkte.
Setze $t_{1} = 1$ in die Geradengleichung ein:
${\vec{X}}_{M_{1}} = (\begin{array}{c} 2 \\ 6 \\ 1 \end{array}) + 1 \cdot (\begin{array}{c} 0 \\ - 4 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 2 \\ 1 \end{array}) \Rightarrow M_{1} (2 | 2 | 1)$
Setze $t_{2} = - 1$ in die Geradengleichung ein:
${\vec{X}}_{M_{2}} = (\begin{array}{c} 2 \\ 6 \\ 1 \end{array}) + (- 1) \cdot (\begin{array}{c} 0 \\ - 4 \\ 0 \end{array}) = (\begin{array}{c} 2 \\ 10 \\ 1 \end{array}) \Rightarrow M_{2} (2 | 10 | 1)$
Antwort: Die beiden Kugeln mit den Mittelpunkten $M_{1} (2 | 2 | 1)$ und $M_{2} (2 | 10 | 1)$ und dem Radius $r = 4$ liegen auf der Geraden $g$ und die Ebene ist eine Tangentialebene.
Der Mittelpunkt $M (m_{1} | m_{2} | m_{3})$ liegt auf der Geraden $g$ . Setze $M$ für $\vec{X}$ in die Geradengleichung ein.
Erstelle von der gegebenen Ebenengleichung $E$ die Hessesche Normalenform. Der Abstand des Mittelpunktes $M$ von der Ebene $E$ muss gleich dem Radius $r$ sein.

Gegeben sind eine Kugel $K$ mit Mittelpunkt $M (3 | - 1 | 2)$ , Radius $r = \sqrt{11}$ und eine Gerade

$g : \vec{X} = (\begin{array}{c} 2 \\ 0 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 2 \\ - 4 \\ - 4 \end{array})$ .

Zeige, dass die Gerade eine Sekante der Kugel ist. Gib auch beide Schnittpunkte an.

Gib für die beiden Schnittpunkte $S_{1}$ und $S_{2}$ jeweils die zugehörende Tangentialebene in Koordinatenform an.

Zeige, dass sich die beiden Tangentialebenen $E_{T_{1}}$ und $E_{T_{2}}$ schneiden und berechne die Gleichung der Schnittgeraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lage zweier Ebenen
Schnitt von $E_{T_{1}}$ und $E_{T_{2}}$
Die beiden Tangentialebenen $E_{T_{1}}$ und $E_{T_{2}}$ haben die beiden Normalenvektoren:
${\vec{n}}_{T_{1}} = (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$ und ${\vec{n}}_{T_{2}} = (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$ .
Die Normalenvektoren sind nicht Vielfache voneinander. Die beiden Ebenen sind somit nicht parallel, d.h. sie schneiden sich.
Berechnung der Schnittgeraden
Die beiden Ebenengleichungen liegen in der Koordinatenform vor. Die Berechnung der Schnittgeraden erfolgt durch Lösen eines Gleichungssystems aus $2$ Gleichungen mit $3$ Unbekannten. Dabei gibt es mehrere Lösungswege z.B. das Einsetzungsverfahren oder das Additionsverfahren. Die Lösung des Gleichungssystems erfolgt hier mit dem Additionsverfahren.
Die Tangentialebene $E_{T_{1}}$ ist Gleichung $(I)$ und die Tangentialebene $E_{T_{2}}$ ist Gleichung $(I I)$ .
Eliminiere eine Variable z.B. die Variable $x_{1}$ .
Rechne $(I) + (I I)$ :
$\begin{array}{l} \begin{array}{cccccccl} (I) : - x_{1} & + & x_{2} & + & 3 x_{3} & = & 13 \\ + (I I) : x_{1} & - & 3 x_{2} & - & x_{3} & = & 15 \end{array} \\ 0 x_{1} - 2 x_{2} + 2 x_{3} = 28 \Rightarrow (I I I) : x_{2} = - 14 + x_{3} \end{array}$
Du hast die Gleichung $(I I I) : x_{2} = - 14 + x_{3}$ erhalten.
Bei $2$ Gleichungen mit $3$ Unbekannten ist eine Unbekannte frei wählbar. Wähle z.B. $x_{3} = s$ .
Somit lautet die Gleichung $(I I I^{'}) : x_{2} = - 14 + s$ .
Setze die Gleichung $(I I I^{'})$ und $x_{3} = s$ in Gleichung $(I I)$ ein.
$(I I) : x_{1} - 3 x_{2} - x_{3}$ $=$ $15$
↓
Setze $x_{2} = - 14 + s$ und $x_{3} = s$ ein.
$x_{1} - 3 \cdot (- 14 + s) - s$ $=$ $15$
↓
Löse die Klammer auf.
$x_{1} + 42 - 3 s - s$ $=$ $15$
↓
Vereinfache.
$x_{1} + 42 - 4 s$ $=$ $15$ $- 42 + 4 s$
$x_{1}$ $=$ $- 27 + 4 s$
Schreibe die drei erhaltenen Gleichungen für $x_{1}$ , $x_{2}$ und $x_{3}$ untereinander und sortiere entsprechend.
$g_{S c h n i t t} : \vec{X} = (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{c} - 27 + 4 s \\ - 14 + s \\ 0 + s \end{array}) = (\begin{array}{c} - 27 \\ - 14 \\ 0 \end{array}) + s (\begin{array}{c} 4 \\ 1 \\ 1 \end{array})$
Antwort: Die Gleichung der Schnittgeraden der beiden Tangentialebenen lautet:
$g_{S c h n i t t} : \vec{X} = (\begin{array}{c} - 27 \\ - 14 \\ 0 \end{array}) + s (\begin{array}{c} 4 \\ 1 \\ 1 \end{array})$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Unter welchen Winkel schneiden sich die beiden Tangentialebenen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zweier Ebenen
Für den Schnittwinkel $α$ zwischen zwei Ebenen gilt folgende Formel:
$\cos α = \frac{| {\vec{n}}_{1} \circ {\vec{n}}_{2} |}{| {\vec{n}}_{1} | \cdot | {\vec{n}}_{2} |}$
Im Zähler des Bruches steht der Betrag des Skalarproduktes der beiden Normalenvektoren ${\vec{n}}_{1}$ und ${\vec{n}}_{2}$ der beiden Tangentialebenen $E_{T_{1}} : - x_{1} + x_{2} + 3 x_{3} = 13$ und $E_{T_{2}} : x_{1} - 3 x_{2} - x_{3} = 15$ . Im Nenner des Bruches steht das Produkt der Beträge der beiden Normalenvektoren.
Lies die Normalenvektoren aus den Koordinatengleichungen ab:
${\vec{n}}_{1} = (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$ und ${\vec{n}}_{2} = (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$
Für den Betrag von ${\vec{n}}_{1}$ gilt: $| {\vec{n}}_{1} | = \sqrt{(- 1)^{2} + 1^{2} + 3^{2}} = \sqrt{1 + 1 + 9} = \sqrt{11}$
Für den Betrag von ${\vec{n}}_{2}$ gilt: $| {\vec{n}}_{2} | = \sqrt{1^{2} + (- 3)^{2} + (- 1)^{2}} = \sqrt{1 + 9 + 1} = \sqrt{11}$
Setze in die oben genannte Formel ein:
$\cos α$ $=$ $\frac{| (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array}) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array}) |}{\sqrt{11} \cdot \sqrt{11}}$
↓
Berechne das Skalarprodukt und vereinfache.
$=$ $\frac{| - 1 - 3 - 3 |}{11}$
↓
Vereinfache.
$=$ $\frac{| - 7 |}{11}$
↓
Berechne den Betrag.
$=$ $\frac{7}{11}$
Du hast die Gleichung $\cos α = \frac{7}{11}$ erhalten. Durch Anwendung der Umkehrfunktion des Kosinus kannst du den Winkel $α$ berechnen.
Hinweis: Benutze auf dem Taschenrechner die Funktion $\cos^{- 1} (x)$ .
$α = \arccos (\frac{7}{11}) \approx {50,48}^{\circ}$
Antwort: Der Schnittwinkel zwischen den beiden Tangentialebenen beträgt rund ${50,5}^{\circ}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Lies die Normalenvektoren aus den Koordinatengleichungen ab und setze sie in die Formel für den Schnittwinkel zweier Ebenen ein.

Gegeben ist eine Kugel $K$ mit $M (- 2 | 3 | - 5)$ , $r = 9$ und ein Punkt $B (2 | 2 | z)$ mit $z > 0$ auf der Kugel.

Berechne die Koordinate $z$ und gib die Gleichung der Tangentialebene $E_{T}$ im Punkt $B$ an.

8
Gegeben ist eine Kugel $K : (x_{1} - 2)^{2} + (x_{2} - 3)^{2} + (x_{3} - 1)^{2} = 16$ .
Die Ebene $E$ enthält den Punkt $P (2 | 5 | - 3)$ . Gib eine Bedingung an, so dass die Ebene $E$ eine Tangentialebene an die Kugel $K$ ist.
Die gesuchte Bedingung enthält den Normaleneinheitsvektor ${\vec{n}}_{0}$ der Ebene $E$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Skalarprodukt zwischen den Vektoren $\vec{P M}$ und ${\vec{n}}_{0}$ ist gleich der Länge der Projektion des Vektors $\vec{P M}$ auf den Einheitsvektor ${\vec{n}}_{0}$ .
Die Länge der Projektion ist in diesem Fall gleich dem Radius $r$ . Es gilt also:
$| \vec{P M} \circ {\vec{n}}_{0} | = r$
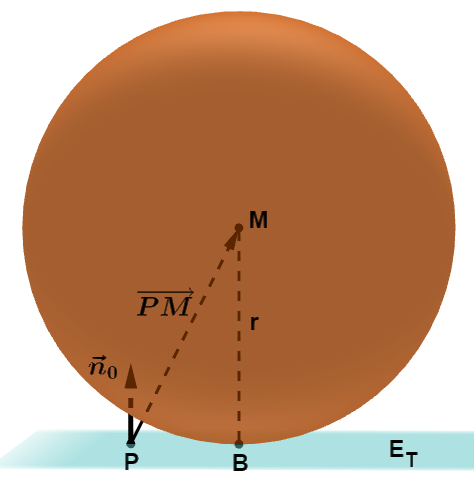
Lies aus der gegebenen Kugelgleichung die Koordinaten des Mittelpunktes $M$ und den Radius $r$ ab:
$M (2 | 3 | 1)$ und $r = \sqrt{16} = 4$ .
Berechne den Vektor $\vec{P M} = \vec{O M} - \vec{O P} = (\begin{array}{c} 2 \\ 3 \\ 1 \end{array}) - (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) = (\begin{array}{c} 0 \\ - 2 \\ 4 \end{array})$ .
Dann folgt für die gesuchte Bedingung: $| \vec{P M} \circ {\vec{n}}_{0} | = r \Rightarrow | (\begin{array}{c} 0 \\ - 2 \\ 4 \end{array}) \circ {\vec{n}}_{0} | = 4$
Antwort: Erfüllt der Normaleneinheitsvektor ${\vec{n}}_{0}$ der Ebene $E$ die folgende Bedingung $| (\begin{array}{c} 0 \\ - 2 \\ 4 \end{array}) \circ {\vec{n}}_{0} | = 4$ , dann ist die Ebene $E$ eine Tangentialebene an die Kugel $K$ und enthält den Punkt $P$ .
Das Skalarprodukt zwischen einem Vektor $\vec{O A}$ und einem Einheitsvektor ${\vec{n}}_{0}$ ist gleich der Länge der Projektion des Vektors $\vec{O A}$ auf den Einheitsvektor ${\vec{n}}_{0}$ . Die Länge dieser Projektion muss gleich dem Kugelradius $r$ sein.
9
Gegeben sind eine Kugel $K$ und eine Ebene $E$ .
$K : (x_{1} - 4)^{2} + (x_{2} - 2)^{2} + (x_{3} + 1)^{2} = 16 und E : 2 x_{1} - 2 x_{2} + x_{3} = u$
Bestimme den Parameter $u$ so, dass die Ebene $E$ eine Tangentialebene an die Kugel $K$ ist. Gib mögliche Berührpunkte an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentialebene
Parameterberechnung
Wenn die Ebene $E$ eine Tangentialebene an die Kugel $K$ sein soll, dann muss der Abstand des Mittelpunktes $M$ von der Ebene $E$ gleich dem Kugelradius $r$ sein.
Lies aus der gegebenen Kugelgleichung die Koordinaten des Mittelpunktes $M$ und den Radius $r$ ab:
$M (4 | 2 | - 1)$ ; $r = \sqrt{16} = 4$
Erstelle eine Hessesche Normalenform der Ebene $E$ :
$E_{H N F} : \frac{2 x_{1} - 2 x_{2} + x_{3} - u}{\sqrt{2^{2} + (- 2)^{2} + 1^{2}}} = \frac{2 x_{1} - 2 x_{2} + x_{3} - u}{\sqrt{9}} = \frac{2 x_{1} - 2 x_{2} + x_{3} - u}{3} = 0$
Berechne den Abstand des Mittelpunktes $M (4 | 2 | - 1)$ von der Ebene $E$ :
$d (M, E) = | \frac{2 \cdot 4 - 2 \cdot 2 - 1 - u}{3} | = | \frac{3 - u}{3} |$
Setze $d (M, E) = r \Rightarrow | \frac{3 - u}{3} | = 4 \Rightarrow | 3 - u | = 4 \cdot 3 = 12$
Fall +
$3 - u = 12 \Rightarrow u_{1} = - 9$
Fall -
$- 3 + u = 12 \Rightarrow u_{2} = 15$
Antwort: Es gibt zwei parallele Tangentialebenen an die Kugel $K$ :
$E_{T_{1}} : 2 x_{1} - 2 x_{2} + x_{3} = - 9$ und $E_{T_{2}} : 2 x_{1} - 2 x_{2} + x_{3} = 15$
Berührpunkte
Aus der nebenstehenden Abbildung kannst du folgende Vektorgleichung entnehmen:
$\vec{O B_{2}} = \vec{O M} + \vec{M B_{2}}$
$\vec{O M} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array})$
$\vec{M B_{2}} = | \vec{M B_{2}} | \cdot {\vec{n}}_{0} = r \cdot {\vec{n}}_{0} = 4 \cdot {\vec{n}}_{0}$
Dabei ist ${\vec{n}}_{0}$ der Normaleneinheitsvektor der Ebene $E$ .
$\vec{n} = (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array})$
$| \vec{n} | = \sqrt{2^{2} + (- 2)^{2} + 1^{2}} = \sqrt{9} = 3$
${\vec{n}}_{0} = \frac{\vec{n}}{| \vec{n} |} = \frac{1}{3} \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array})$
$\vec{O B_{2}} = \vec{O M} + \vec{M B_{2}} = \vec{O M} + 4 \cdot {\vec{n}}_{0} = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + 4 \cdot \frac{1}{3} \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array}) = (\begin{array}{c} 4 + \frac{8}{3} \\ 2 - \frac{8}{3} \\ - 1 + \frac{4}{3} \end{array}) = (\begin{array}{c} \frac{20}{3} \\ - \frac{2}{3} \\ \frac{1}{3} \end{array})$
Entsprechend gilt:
$\vec{O B_{1}} = \vec{O M} + \vec{M B_{1}} = \vec{O M} + 4 \cdot (- {\vec{n}}_{0}) = (\begin{array}{c} 4 \\ 2 \\ - 1 \end{array}) + 4 \cdot \frac{1}{3} \cdot (\begin{array}{c} - 2 \\ 2 \\ - 1 \end{array}) = (\begin{array}{c} 4 - \frac{8}{3} \\ 2 + \frac{8}{3} \\ - 1 - \frac{4}{3} \end{array}) = (\begin{array}{c} \frac{4}{3} \\ \frac{14}{3} \\ - \frac{7}{3} \end{array})$
Antwort: Die beiden Berührpunkte haben die Koordinaten $B_{1} (\frac{4}{3} | \frac{14}{3} | - \frac{7}{3})$ und $B_{2} (\frac{20}{3} | - \frac{2}{3} | \frac{1}{3})$ .
Bei einer Tangentialebene ist der Abstand des Kugelmittelpunktes $M$ von der Ebene $E$ gleich dem Kugelradius $r$ . Erstelle eine Hessesche Normalenform der Ebene $E$ und berechne den Abstand $d (M, E)$ . Die Berührpunkte kannst du über eine Vektorgleichung ermitteln: $\vec{O B} = \vec{O M} + \vec{M B}$
Dabei ist $\vec{M B} = | \vec{M B} | \cdot {\vec{n}}_{0} = r \cdot {\vec{n}}_{0}$ und ${\vec{n}}_{0}$ ist der Normaleneinheitsvektor der Ebene $E$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

${((\begin{array}{c} 2 \\ 0 \\ 5 \end{array}) + t \cdot (\begin{array}{c} 2 \\ - 4 \\ - 4 \end{array}) - (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}))}^{2}$	$=$	$11$
	↓	Fasse zusammen.
${((\begin{array}{c} - 1 \\ 1 \\ 3 \end{array}) + t \cdot (\begin{array}{c} 2 \\ - 4 \\ - 4 \end{array}))}^{2}$	$=$	$11$
	↓	Vereinfache weiter.
${(\begin{array}{c} - 1 + 2 t \\ 1 - 4 t \\ 3 - 4 t \end{array})}^{2}$	$=$	$11$
	↓	Rechne das Skalarprodukt aus.
$(- 1 + 2 t)^{2} + (1 - 4 t)^{2} + (3 - 4 t)^{2}$	$=$	$11$
	↓	Löse die Klammern auf und vergiss dabei nicht die binomische Formel anzuwenden.
$1 - 4 t + 4 t^{2} + 1 - 8 t + 16 t^{2} + 9 - 24 t + 16 t^{2}$	$=$	$11$
	↓	Fasse die linke Seite zusammen.
$36 t^{2} - 36 t + 11$	$=$	$11$	$- 11$
$36 t^{2} - 36 t$	$=$	$0$	$36 t ausklammern$
$36 t \cdot (t - 1)$	$=$	$0$

$K : (\vec{x} - \vec{m})^{2}$	$=$	$r^{2}$
	↓	Setze den Mittelpunkt $M (- 2 \| 3 \| - 5)$ und $r = 9$ ein.
${(\vec{x} - (\begin{array}{c} - 2 \\ 3 \\ - 5 \end{array}))}^{2}$	$=$	$9^{2}$

${((\begin{array}{c} 2 \\ 2 \\ z \end{array}) - (\begin{array}{c} - 2 \\ 3 \\ - 5 \end{array}))}^{2}$	$=$	$81$
	↓	Vereinfache.
${(\begin{array}{c} 4 \\ - 1 \\ z + 5 \end{array})}^{2}$	$=$	$81$
	↓	Berechne das Skalarprodukt.
$4^{2} + (- 1)^{2} + (z + 5)^{2}$	$=$	$81$
	↓	Berechne die Quadrate und vergiss nicht die binomische Formel anzuwenden.
$16 + 1 + z^{2} + 10 z + 25$	$=$	$81$
	↓	Fasse die linke Seite zusammen.
$z^{2} + 10 z + 42$	$=$	$81$	$- 81$
$z^{2} + 10 z - 39$	$=$	$0$

$E_{H N F} : \frac{3 x_{1} + x_{2} - 2 x_{3} - 16}{\sqrt{3^{2} + 1^{2} + (- 2)^{2}}}$	$=$	$0$
	↓	Berechne die Wurzel.
$E_{H N F} : \frac{3 x_{1} + x_{2} - 2 x_{3} - 16}{\sqrt{14}}$	$=$	$0$

$d (M, E)$	$=$	$\| \frac{3 \cdot 4 + 0 - 2 \cdot 5 - 16}{\sqrt{14}} \|$
	↓	vereinfache
	$=$	$\| \frac{- 14}{\sqrt{14}} \|$
	↓	Berechne den Betrag.
	$=$	$\frac{14}{\sqrt{14}}$
	↓	Vereinfache weiter, indem du $14$ durch $\sqrt{14} \cdot \sqrt{14}$ ersetzt.
	$=$	$\frac{\sqrt{14} \cdot \sqrt{14}}{\sqrt{14}}$
	↓	Kürze den Bruch.
	$=$	$\sqrt{14}$

$E : 3 x_{1} + x_{2} - 2 x_{3}$	$=$	$16$
	↓	Setze $g$ in $E$ ein.
$3 \cdot (4 + 3 t) + t - 2 \cdot (5 - 2 t)$	$=$	$16$
	↓	Löse die Klammern auf.
$12 + 9 t + t - 10 + 4 t$	$=$	$16$
	↓	Vereinfache die linke Seite.
$14 t + 2$	$=$	$16$	$- 2$
	↓	Löse nach $t$ auf.
$14 t$	$=$	$14$	$: 14$
$t$	$=$	$1$

$E_{T_{1}} : (\vec{x} - \vec{b}) \circ (\vec{b} - \vec{m})$	$=$	$0$
	↓	Setze für $B$ die Koordinaten des ersten Schnittpunktes $S_{1} (2 \| 0 \| 5)$ ein. Setze den Mittelpunkt $M (3 \| - 1 \| 2)$ ein.
$(\vec{x} - (\begin{array}{c} 2 \\ 0 \\ 5 \end{array})) \circ ((\begin{array}{c} 2 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}))$	$=$	$0$
	↓	Vereinfache.
$(\vec{x} - (\begin{array}{c} 2 \\ 0 \\ 5 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$	$=$	$0$
	↓	Diese Gleichung ist die Normalengleichung der Ebene.
$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 2 \\ 0 \\ 5 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$	$=$	$0$
	↓	Vereinfache
$(\begin{array}{c} x_{1} - 2 \\ x_{2} - 0 \\ x_{3} - 5 \end{array}) \circ (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array})$	$=$	$0$
	↓	Um die Koordinatengleichung zu erhalten, rechne das Skalarprodukt aus.
$(x_{1} - 2) \cdot (- 1) + x_{2} \cdot 1 + (x_{3} - 5) \cdot 3$	$=$	$0$
	↓	Löse die Klammern auf.
$- x_{1} + 2 + x_{2} + 3 x_{3} - 15$	$=$	$0$
	↓	Vereinfache.
$- x_{1} + x_{2} + 3 x_{3} - 13$	$=$	$0$

$E_{T_{1}} : (\vec{x} - \vec{b}) \circ (\vec{b} - \vec{m})$	$=$	$0$
	↓	Setze für $B$ die Koordinaten des zweiten Schnittpunktes $S_{2} (4 \| - 4 \| 1)$ ein. Setze den Mittelpunkt $M (3 \| - 1 \| 2)$ ein.
$(\vec{x} - (\begin{array}{c} 4 \\ - 4 \\ 1 \end{array})) \circ ((\begin{array}{c} 4 \\ - 4 \\ 1 \end{array}) - (\begin{array}{c} 3 \\ - 1 \\ 2 \end{array}))$	$=$	$0$
	↓	Vereinfache.
$(\vec{x} - (\begin{array}{c} 4 \\ - 4 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$	$=$	$0$
	↓	Diese Gleichung ist die Normalengleichung der Ebene.
$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 4 \\ - 4 \\ 1 \end{array})) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$	$=$	$0$
	↓	Vereinfache.
$(\begin{array}{c} x_{1} - 4 \\ x_{2} + 4 \\ x_{3} - 1 \end{array}) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array})$	$=$	$0$
	↓	Um die Koordinatengleichung zu erhalten, rechne das Skalarprodukt aus.
$(x_{1} - 4) \cdot 1 + (x_{2} + 4) \cdot (- 3) + (x_{3} - 1) \cdot (- 1)$	$=$	$0$
	↓	Löse die Klammern auf.
$x_{1} - 4 - 3 x_{2} - 12 - x_{3} + 1$	$=$	$0$
	↓	Vereinfache.
$x_{1} - 3 x_{2} - x_{3} - 15$	$=$	$0$

$(I I) : x_{1} - 3 x_{2} - x_{3}$	$=$	$15$
	↓	Setze $x_{2} = - 14 + s$ und $x_{3} = s$ ein.
$x_{1} - 3 \cdot (- 14 + s) - s$	$=$	$15$
	↓	Löse die Klammer auf.
$x_{1} + 42 - 3 s - s$	$=$	$15$
	↓	Vereinfache.
$x_{1} + 42 - 4 s$	$=$	$15$	$- 42 + 4 s$
$x_{1}$	$=$	$- 27 + 4 s$

$\cos α$	$=$	$\frac{\| (\begin{array}{c} - 1 \\ 1 \\ 3 \end{array}) \circ (\begin{array}{c} 1 \\ - 3 \\ - 1 \end{array}) \|}{\sqrt{11} \cdot \sqrt{11}}$
	↓	Berechne das Skalarprodukt und vereinfache.
	$=$	$\frac{\| - 1 - 3 - 3 \|}{11}$
	↓	Vereinfache.
	$=$	$\frac{\| - 7 \|}{11}$
	↓	Berechne den Betrag.
	$=$	$\frac{7}{11}$

$z_{1,2}$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	↓	Setze $p = 10$ und $q = - 39$ ein.
	$=$	$- \frac{10}{2} \pm \sqrt{{(\frac{10}{2})}^{2} - (- 39)}$
	↓	Vereinfache.
	$=$	$- 5 \pm \sqrt{5^{2} + 39}$
	$=$	$- 5 \pm \sqrt{64}$
	$=$	$- 5 \pm 8$

$E_{T} : (\vec{x} - \vec{b}) \circ (\vec{b} - \vec{m})$	$=$	$0$
	↓	Setze $B (2 \| 2 \| 3)$ und $M (- 2 \| 3 \| - 5)$ ein.
$(\vec{x} - (\begin{array}{c} 2 \\ 2 \\ 3 \end{array})) \circ ((\begin{array}{c} 2 \\ 2 \\ 3 \end{array}) - (\begin{array}{c} - 2 \\ 3 \\ - 5 \end{array}))$	$=$	$0$
	↓	Vereinfache.
$(\vec{x} - (\begin{array}{c} 2 \\ 2 \\ 3 \end{array})) \circ (\begin{array}{c} 4 \\ - 1 \\ 8 \end{array})$	$=$	$0$
	↓	Diese Gleichung ist die Normalengleichung der Ebene.
$((\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 2 \\ 2 \\ 3 \end{array})) \circ (\begin{array}{c} 4 \\ - 1 \\ 8 \end{array})$	$=$	$0$
	↓	Vereinfache.
$(\begin{array}{c} x_{1} - 2 \\ x_{2} - 2 \\ x_{3} - 3 \end{array}) \circ (\begin{array}{c} 4 \\ - 1 \\ 8 \end{array})$	$=$	$0$
	↓	Um die Koordinatengleichung zu erhalten, rechne das Skalarprodukt aus.
$(x_{1} - 2) \cdot 4 + (x_{2} - 2) \cdot (- 1) + (x_{3} - 3) \cdot 8$	$=$	$0$
	↓	Löse die Klammern auf.
$4 x_{1} - 8 - x_{2} + 2 + 8 x_{3} - 24$	$=$	$0$
	↓	Fasse zusammen.
$4 x_{1} - x_{2} + 8 x_{3} - 30$	$=$	$0$

Aufgaben zu Kugeln, Ebenen und Tangentialebenen

Teilaufgabe 1

Bestimmung der Art des Schnitts von Ebene und Kugel

Berechnung des Mittelpunktes M′ des Schnittkreises

Bestimmung des Radius des Schnittkreises

Zusätzliche Zeichnung zur Veranschaulichung

Teilaufgabe 2

Teilaufgabe 3

Teilaufgabe 4

Zusätzliche Visualisierung

Strategie zu Teilaufgabe 1

Strategie zu Teilaufgabe 2

Strategie zu Teilaufgabe 3

Strategie zu Teilaufgabe 4

Teilaufgabe 1

Bestimmung der Art des Schnitts von Ebene und Kugel

Berechnung des Berührpunktes B

Teilaufgabe 2

Bestimmung der hessischen Normalenform der Ebenenschar Fa

Bestimmung des Parameter a, so dass der Schnittkreisradius r=2,2 beträgt

Bestimmung des Mittelpunktes M′des Schnittkreises

Teilaufgabe 3

Berechnung der Tangentialebenengleichung E2

Teilaufgabe 4

Berechnung der Schnittgeraden der Ebenen E1 und E2

Teilaufgabe 5

Berechnung der Länge der Strecke, die die Kugel vom Startpunkt aus zurücklegt

Strategie zu Teilaufgabe 1

Strategie zu Teilaufgabe 2

Strategie zu Teilaufgabe 3

Strategie zu Teilaufgabe 4

Strategie zu Teilaufgabe 5

Berechnung des Berührpunktes:

Aufstellen der Kugelgleichung

Schnittpunkte berechnen

Hast du eine Frage oder Feedback?

Aufstellen der Tangentialebenengleichung im Punkt S1

Aufstellen der Tangentialebenengleichung im Punkt S2

Hast du eine Frage oder Feedback?

Schnitt von ET1 und ET2

Berechnung der Schnittgeraden

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Aufstellen der Kugelgleichung

Kugel K:

Tangentialebene ET

Parameterberechnung

Berührpunkte

Berechnung des Mittelpunktes $M^{'}$ des Schnittkreises

Berechnung des Berührpunktes $B$

Bestimmung der hessischen Normalenform der Ebenenschar $F_{a}$

Bestimmung des Parameter $a$ , so dass der Schnittkreisradius $r = 2,2$ beträgt

Bestimmung des Mittelpunktes $M^{'}$ des Schnittkreises

Berechnung der Tangentialebenengleichung $E_{2}$

Berechnung der Schnittgeraden der Ebenen $E_{1}$ und $E_{2}$

Aufstellen der Tangentialebenengleichung im Punkt $S_{1}$

Aufstellen der Tangentialebenengleichung im Punkt $S_{2}$

Schnitt von $E_{T_{1}}$ und $E_{T_{2}}$

Kugel $K$ :

Tangentialebene $E_{T}$