Gegeben ist die in definierte Funktion . Abb. 1 zeigt den Graphen von , der die -Achse als waagrechte Asymptote besitzt.
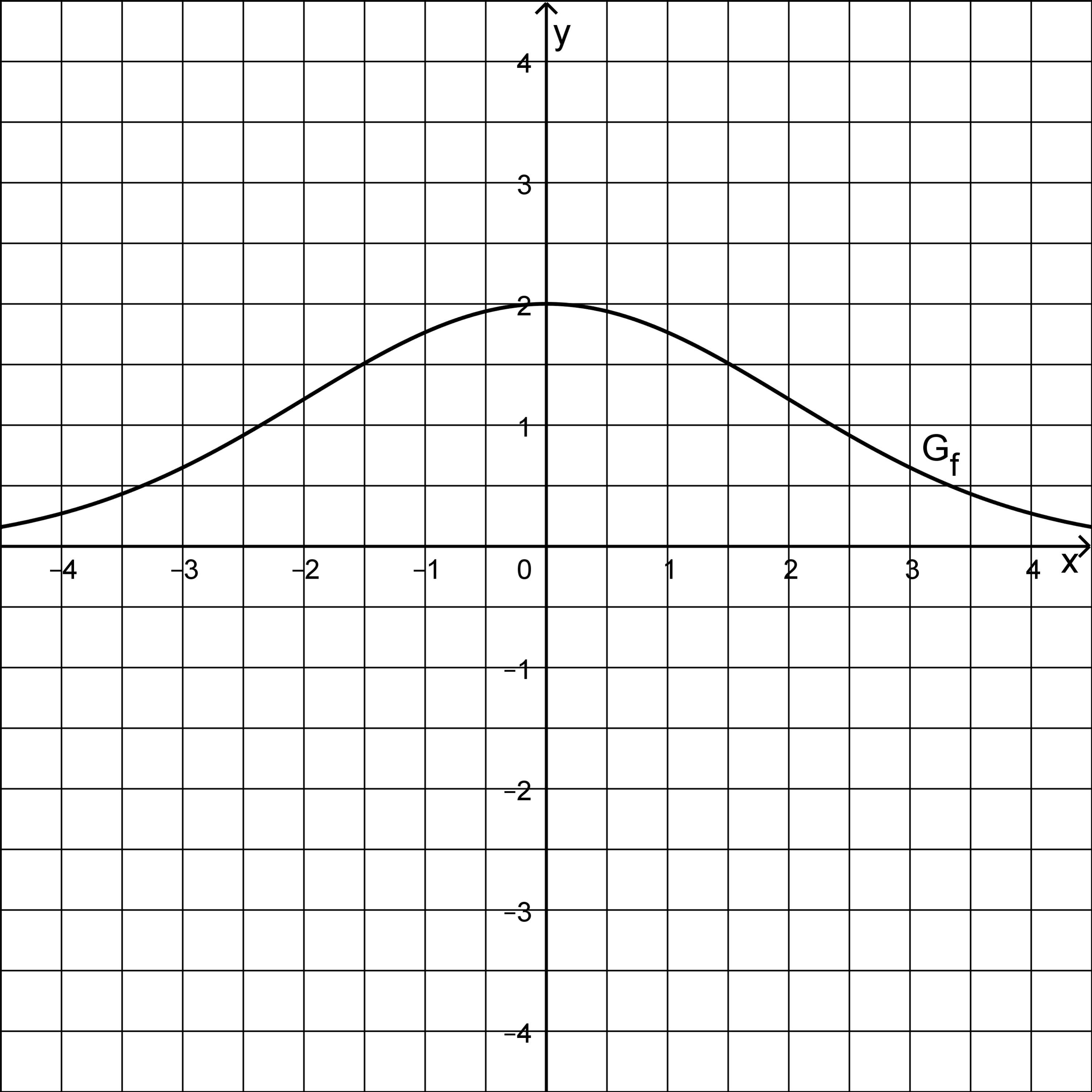
Abb. 1
Berechnen Sie die Koordinaten des Schnittpunkts von mit der y-Achse und weisen Sie rechnerisch nach, dass symmetrisch bezüglich der y-Achse ist. (2 P)
Der Punkt ist einer der beiden Wendepunkte von . Die Tangente an im Punkt wird mit bezeichnet. Ermitteln Sie eine Gleichung von und berechnen Sie die Stelle an der die x-Achse schneidet. (5 P)
(zur Kontrolle: )
Betrachtet wird für jeden Wert das Rechteck mit den Eckpunkten und .
Zeichnen Sie für das Rechteck in Abb. 1 ein. (1 P)
Berechnen Sie denjenigen Wert von , für den gilt. (3 P)
Geben Sie in Abhängigkeit von die Seitenlängen des Rechtecks an und begründen Sie, dass der Flächeninhalt des Rechtecks durch den Term
gegeben ist. (3 P)
Es gibt einen Wert von , für den der Flächeninhalt des Rechtecks maximal ist. Berechnen Sie diesen Wert von . (4 P)
Betrachtet werden für die in definierten Funktionen
. Somit gilt wobei sich und im Definitionsbereich unterscheiden.
Begründen Sie mithilfe der ersten Ableitung von , dass für jeden Wert von umkehrbar ist. Skizzieren Sie in Abbildung 1 den Graphen der Umkehrfunktion von (4 P)
Geben Sie alle Werte von an, für die der Graph von und der Graph der Umkehrfunktion von keinen gemeinsamen Punkt haben. (2 P)


