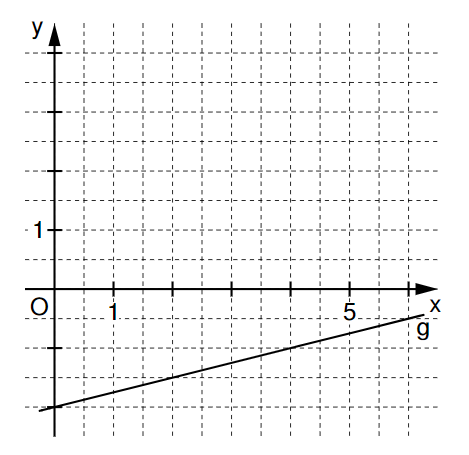Dreieckskonstruktion

Der Punkt $A$ ist der Koordinatenursprung $A(0|0)$.

Setze $x=4$ in die Geradengleichung ein, um die Koordinaten des Punktes $B_1$ zu erhalten: $y(4)=\mathrm{0,25}\cdot 4-2=-1$$\Rightarrow$$B_1(4|-1)$.

Zeichne die Strecke $\overline{A{B}_1}$ und trage im Punkt $A$ den Winkel $\measuredangle B_{1}A{C}_1={50}^{\circ }$ ab.

Weiterhin gilt: $\overline{A{C}_1}=\mathrm{1,5}\cdot \overline{A{B}_1}$.

Zeichne zunächst um $A$ einen Kreis mit dem Radius $r=|\overline{A{B}_1}|$.

Der Kreis schneidet den freien Schenkel des Winkels $\measuredangle B_{1}A{C}_1$ im Punkt $S$.

Die halbe Länge der Strecke $\overline{A{B}_1}$ erhältst du durch Konstruktion der Mittelsenkrechten auf der Strecke $\overline{A{B}_1}$. (Aus Gründen der Übersichtlichkeit ist diese Konstruktion hier nicht eingezeichnet.)

Der Schnittpunkt der Mittelsenkrechten mit der Strecke $\overline{A{B}_1}$ ist der Punkt $M.$ Nimm die Strecke $\overline{AM}$ in den Zirkel und zeichne um $S$ einen weiteren Kreis mit dem Radius $r=|\overline{AM}|$. Der Kreis schneidet den freien Schenkel des Winkels $\measuredangle B_{1}A{C}_1$ im Punkt $C_1$.

Verbinde den Punkt $C_1$ mit $B_1$ und das Dreieck $A{B}_1{C}_1$ ist fertig.

Für $x=8\Rightarrow y(8)=\mathrm{0,25}\cdot 8-2=0$

Der Punkt $B_2$ hat die Koordinaten $B_2(8|0)$ und der Vektor $\overrightarrow{A{B}_2}=\left(\begin{array}{c}8\\ 0\end{array}\right)$.

Drehe den Vektor $\overrightarrow{A{B}_2}$ um ${50}^{\circ }$ um den Ursprung und verlängere den Vektor mit dem Faktor $\mathrm{1,5}$ (es gilt: $\overline{A{C}_2}=\mathrm{1,5}\cdot \overline{A{B}_2}$). Benutze dazu die folgende Drehmatrix:

$\begin{array}{rcl}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \mathrm{1,5}\cdot \left(\begin{array}{cc}\cos 50°& -\sin 50°\\ \sin 50°& \cos 50°\end{array}\right)\cdot \left(\begin{array}{c}8\\ 0\end{array}\right)\\ & & \\ & =& \mathrm{1,5}\cdot \left(\begin{array}{c}\cos 50°\cdot 8-\sin 50°\cdot 0\\ \sin 50°\cdot 8+\cos 50°\cdot 0\end{array}\right)\\ & & \\ & =& \left(\begin{array}{c}\mathrm{1,5}\cdot \cos 50°\cdot 8\\ \mathrm{1,5}\cdot \sin 50°\cdot 8\end{array}\right)\end{array}$

Gerundet auf zwei Stellen nach dem Komma.

$\begin{array}{rcl}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& \approx & \left(\begin{array}{c}\mathrm{7,71}\\ \mathrm{9,19}\end{array}\right)\end{array}$

Die Koordinaten des Punktes $C_2$ lauten: $C_2(\mathrm{7,71}|\mathrm{9,19})$.​