Teil B - lernen mit Serlo!

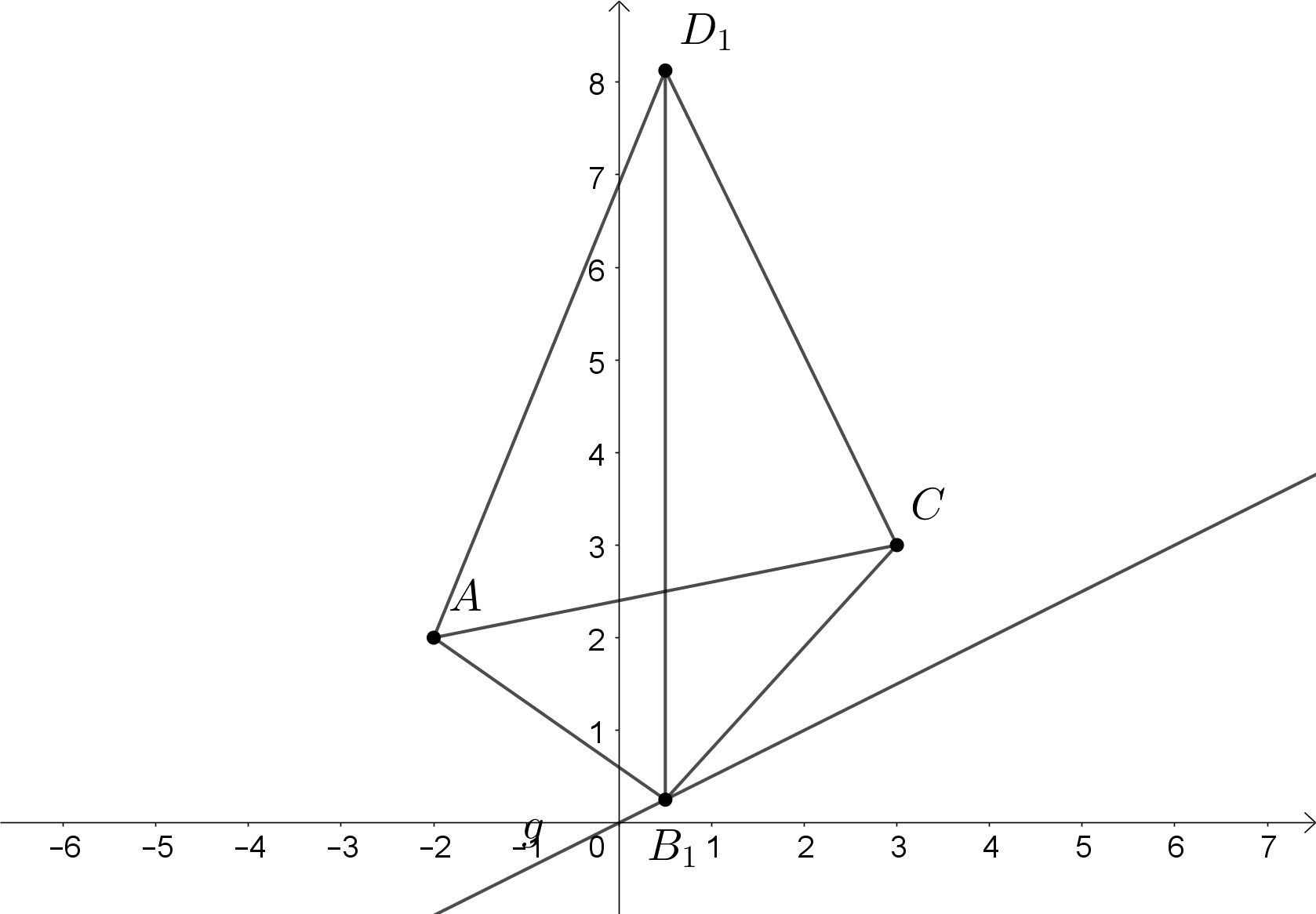
Die Punkte $A (- 2 | 2)$ und $C (3 | 3)$ sind für $x < 8$ gemeinsame Eckpunkte von Vierecken $A B_{n} C D_{n}$ . Die Eckpunkte $B_{n} (x | 0,5 x)$ liegen auf der Geraden $g$ mit der Gleichung $y = 0,5 x; (𝔾 = ℝ$ $\times$ $ℝ)$ . Der Punkt $M$ ist der Mittelpunkt der Diagonalen $[A C]$ .

Für die Diagonalen $[B_{n} D_{n}]$ gilt: $M \in [B_{n} D_{n}]$ und $\vec{B_{n} D_{n}} = 3,5 \cdot \vec{B_{n} M}$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Zeichnen Sie die Gerade $g$ und das Viereck $A B_{1} C D_{1}$ für $x = 0,5$ sowie die Diagonalen $[A C]$ und $[B_{1} D_{1}]$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1$ cm; $- 5 \leq x \leq 5; - 2 \leq y \leq 10$

Für $x = 0,5$ ergibt sich der Punkt $B_{1} (0,5 | 0,25)$ . Um den Punkt $D_{1}$ zu bestimmen, betrachten wir die angegebene Gleichung $\vec{B_{n} D_{n}} = 3,5 \cdot \vec{B_{n} M}$ . Aus dieser wollen wir den Punkt $D_{1}$ bestimmen. Dazu berechnen wir zunächst die Koordinaten von $M$ . Dieser Punkt ist der Mittelpunkt der Diagonalen $[A C]$ . Seine Koordinaten berechnen sich zu:
$x_{M} = \frac{- 2 + 3}{2} = \frac{1}{2}, y_{M} = \frac{2 + 3}{2} = \frac{5}{2},$
sodass wir finden: $M (0,5 | 2,5)$ .
Damit kannst du nun die Koordinaten von $D_{1}$ berechnen. Es gilt
$\vec{O D_{1}} - \vec{O B_{1}} = 3,5 \cdot (\vec{O M} - \vec{O B_{1}})$
beziehungsweise äquivalent
$\vec{O D_{1}} = 3,5 \cdot (\vec{O M} - \vec{O B_{1}}) + \vec{O B_{1}},$
also
$\vec{O D_{1}} = 3,5 \cdot ((\begin{array}{c} 0,5 \\ 2,5 \end{array}) - (\begin{array}{c} 0,5 \\ 0,25 \end{array})) + (\begin{array}{c} 0,5 \\ 0,25 \end{array}) = (\begin{array}{c} 0,5 \\ 8,125 \end{array}) .$
Also ist $D_{1} (0,5 | 8,125)$ .
Bemerkung: Diese Aufgabe ist ein schönes Beispiel dafür, dass es sich manchmal lohnen kann, die Aufgabenstellung erst vollständig zu lesen. Die Berechnung von $D_{1}$ ist zwar für die Skizze notwendig, aber in Teilaufgabe a) gar nicht explizit verlangt. Selbstverständlich kann man die Koordinaten wie oben gezeigt ausrechnen, wer jedoch Teilaufgabe b) gelesen hat, kann auch einfach das dort angegebene Ergebnis nutzen und $x = 0,5$ einsetzen und erhält so direkt die Koordinaten von $D_{1}$ .
Mit diesen Ergebnissen lässt sich die Skizze bereits anfertigen und sollte bei dir so aussehen.
Wie man Geraden in ein Koordinatensystem einzeichnet, kannst du hier nochmal nachlesen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnen Sie die Koordinaten der Punkte $D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ .
[Ergebnis: $D_{n} (- 2,5 x + 1,75 | - 1,25 x + 8,75)$ ]

Hier kannst du genau wie in Teilaufgabe a) vorgehen, nur dass du dieses Mal ein wenig allgemeiner rechnen musst.
Die Koordinaten des Mittelpunktes $M$ bleiben gleich, da sich die Punkte $A$ und $C$ nicht ändern und damit auch nicht ihre Diagonale. Es ist also nach wie vor $M (0,5 | 2,5)$ .
Damit kannst du nun die Koordinaten von $D_{n}$ berechnen. Es gilt
$\vec{O D_{n}} - \vec{O B_{n}} = 3,5 \cdot (\vec{O M} - \vec{O B_{n}})$
beziehungsweise äquivalent
$\vec{O D_{n}} = 3,5 \cdot (\vec{O M} - \vec{O B_{n}}) + \vec{O B_{n}},$
also
$\vec{O D_{n}} = 3,5 \cdot ((\begin{array}{c} 0,5 \\ 2,5 \end{array}) - (\begin{array}{c} x \\ 0,5 x \end{array})) + (\begin{array}{c} x \\ 0,5 x \end{array}) = (\begin{array}{c} - 2,5 x + 1,75 \\ - 1,25 x + 8,75 \end{array}) .$
Also ist $D_{n} (- 2,5 x + 1,75 | - 1,25 x + 8,75)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimmen Sie die Gleichung des Trägergraphen der Punkte $D_{n}$ .

Aus der letzten Teilaufgabe weißt du, dass $D_{n} (- 2,5 x + 1,75 | - 1,25 x + 8,75)$ gilt.
Das bedeutet ganz konkret
$x_{D_{n}} = - 2,5 x + 1,75$
und
$y_{D_{n}} = - 1,25 x + 8,75.$
Löst du die Gleichung der $x$ -Koordinate $x_{D_{n}}$ nach der Variablen $x$ auf, ergibt sich
$\frac{x_{D_{n}} - 1,75}{- 2,5} = x .$
Einsetzen von $x$ in die Gleichung für $y_{D_{n}}$ liefert schließlich
$y_{D_{n}} = - 1,25 \cdot (\frac{x_{D_{n}} - 1,75}{- 2,5}) + 8,75 = 0,5 \cdot x_{D_{n}} + 7,88.$
Die Gleichung des Trägergraphen der Punkte $D_{n}$ lautet also
$y = 0,5 x + 7,88.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Unter den Vierecken $A B_{n} C D_{n}$ gibt es das Drachenviereck $A B_{2} C D_{2}$ .
Zeigen Sie rechnerisch, dass für die $x$ -Koordinate des Punktes $B_{2}$ gilt: $x = 0,91$ .
Berechnen Sie sodann den Flächeninhalt des Drachenvierecks $A B_{2} C D_{2}$ .

Für diese Teilaufgabe musst du dich an eine besondere Eigenschaft von Drachenvierecken erinnern. In einem Drachenviereck stehen die Diagonalen senkrecht aufeinander oder mit anderen Worten: sie bilden einen rechten Winkel. Aus dieser Eigenschaft ist es möglich, folgende Bedingung ableiten:
$\vec{B_{n} M} \circ \vec{A C} = 0.$
Die in dieser Gleichung vorkommenden Vektoren kannst du genauer angeben:
$\vec{A C} = (\begin{array}{c} 3 \\ 3 \end{array}) - (\begin{array}{c} - 2 \\ 2 \end{array}) = (\begin{array}{c} 3 - (- 2) \\ 3 - 2 \end{array}) = (\begin{array}{c} 5 \\ 1 \end{array})$
und
$\vec{B_{n} M} = (\begin{array}{c} 0,5 \\ 2,5 \end{array}) - (\begin{array}{c} x \\ 0,5 x \end{array}) = (\begin{array}{c} 0,5 - x \\ 2,5 - 0,5 x \end{array}) .$
Berechnest du nun das Skalarprodukt dieser beiden Vektoren und setzt das Ergebnis wie in der ersten Gleichung gefordert gleich null, so erhältst du
$(0,5 - x) \cdot 5 + (2,5 - 0,5 x) \cdot 1 = 0.$
Hier kannst du den ersten Summanden ausmultiplizieren und die Terme mit $x$ und die Terme ohne $x$ zusammenfassen. Es bleibt stehen:
$2,5 - 5 x + 2,5 - 0,5 x = 5 - 5,5 x = 0.$
Also muss $5 - 5,5 x = 0$ erfüllt sein. Stellst du diese Gleichung nach $x$ um, so erhältst du
$x = \frac{5}{5,5} = 0,91.$
$𝕃 = {0,91}$
Im zweiten Teil dieser Teilaufgabe soll nun noch der Flächeninhalt des Drachenvierecks $A B_{2} C D_{2}$ berechnet werden.
Hierfür kann einfach die Flächeninhaltsformel für ein Drachenviereck verwendet werden. Sie lautet in unserem Fall unter Ausnutzung von $B_{n} D_{n} = 3,5 \cdot B_{n} M$ :
$A_{A B_{2} C D_{2}} = \frac{1}{2} \cdot A C \cdot B_{2} D_{2} = \frac{1}{2} \cdot A C \cdot 3,5 \cdot B_{2} M .$
Um konkrete Zahlenwerte in die Formel einsetzen zu können, musst du nun die in der Formel vorkommenden Seitenlängen berechnen. Es gilt
$A C = \sqrt{5^{2} + 1^{2}} = \sqrt{26} = 5,10 LE$
und
$B_{2} M = \sqrt{(0,5 - 0,91)^{2} + (2,5 - 0,5 \cdot 0,91)^{2}} = \sqrt{4,35} = 2,09 LE .$
Der Flächeninhalt berechnet sich also zu:
$A_{A B_{2} C D_{2}} = \frac{1}{2} \cdot 5,10 LE \cdot 3,5 \cdot 2,09 LE = 18,65 FE .$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
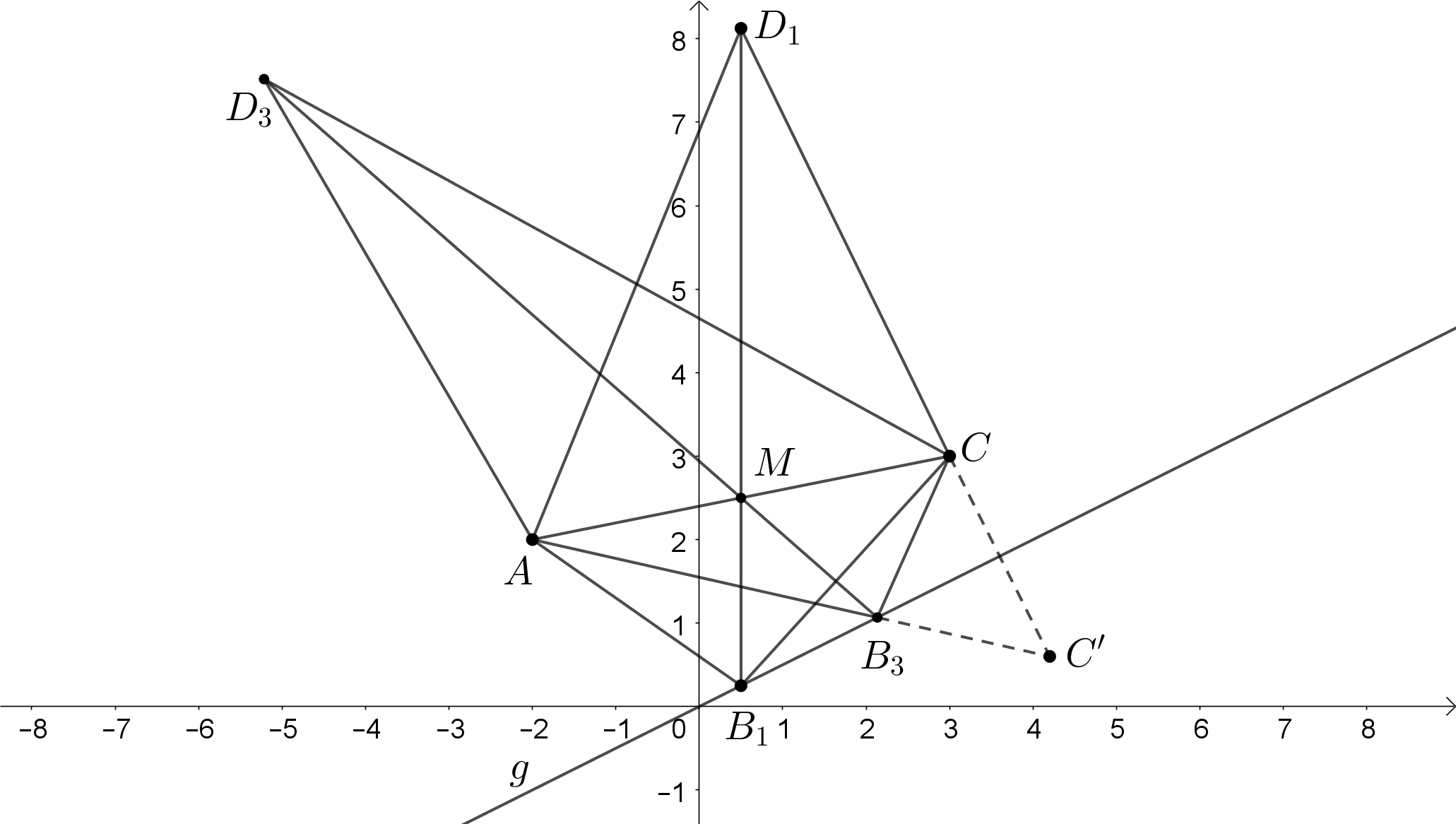
Der Punkt $C^{'}$ entsteht durch Achsenspiegelung des Punktes $C$ an der Geraden $g$ . Für das Viereck $A B_{3} C D_{3}$ gilt: $B_{3} \in [A C^{'}]$ .
Berechnen Sie die Koordinaten von $C^{'}$ und zeichnen Sie sodann das Viereck $A B_{3} C D_{3}$ in das Koordinatensystem zu Teilaufgabe a) ein.

Die Gerade $g$ beschreibt eine Ursprungsgerade, die zur $x$ -Achse den Winkel $φ = \tan^{- 1} (0,5) = 26,57 °$ einschließt.
Die Koordinaten des Punktes $C^{'} (x^{'} | y^{'})$ berechnen sich somit mithilfe der Spiegelungsmatrix für Spiegelungen an Ursprungsgeraden zu
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos (2 \cdot 26,57 °) & \sin (2 \cdot 26,57 °) \\ \sin (2 \cdot 26,57 °) & - \cos (2 \cdot 26,57 °) \end{array}) \cdot (\begin{array}{c} 3 \\ 3 \end{array}) = (\begin{array}{c} 4,2 \\ 0,6 \end{array})$
$C^{'} (4,2 | 0,6)$
Zeichnen wir den so berechneten Punkt $C^{'}$ und das Viereck $A B_{3} C D_{3}$ in die Skizze aus Teilaufgabe a) ein, so ergibt sich folgende erweiterte Skizze. Der Punkt $B_{3}$ ergibt sich dabei als Schnittpunkt der Geraden $g$ mit der Verbindungsstrecke der Punkte $A$ und $C^{'}$ . Der Punkt $D_{3}$ ergibt sich über die in der Aufgabenstellung angegebene Beziehung $\vec{B_{n} D_{n}} = 3,5 \cdot \vec{B_{n} M}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründen Sie, dass für die Flächeninhalte der Dreiecke $A M D_{n}$ und $M B_{n} C$ gilt:
$A_{A M D_{n}} : A_{M B_{n} C} = 2,5 : 1.$

Um diese Teilaufgabe zu lösen, musst du die Flächeninhalte der angegebenen Dreiecke berechnen. Dabei solltest du beachten, dass es sich hier nicht um rechtwinklige Dreiecke handelt und wir daher die allgemeine Flächeninhaltsformel für Dreiecke verwenden müssen.
Der Flächeninhalt der Dreiecke $M B_{n} C$ berechnet sich zu
$A_{M B_{n} C} = \frac{1}{2} \cdot M C \cdot M B_{n} \cdot \sin (∠ B_{n} M C),$
während sich der Flächeninhalt der Dreiecke $A M D_{n}$ berechnen lässt, zu
$A_{A M D_{n}} = \frac{1}{2} \cdot \underset{M C}{\underset{⏟}{A M}} \cdot \underset{(3,5 - 1) \cdot M B_{n}}{\underset{⏟}{M D_{n}}} \cdot \underset{\sin (∠ B_{n} M C)}{\underset{⏟}{\sin (∠ D_{n} M A)}} .$
Also berechnet sich das Verhältnis gerade zu
$\frac{A_{A M D_{n}}}{A_{M B_{n} C}} = \frac{2,5}{1} .$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?