Teil A - lernen mit Serlo!

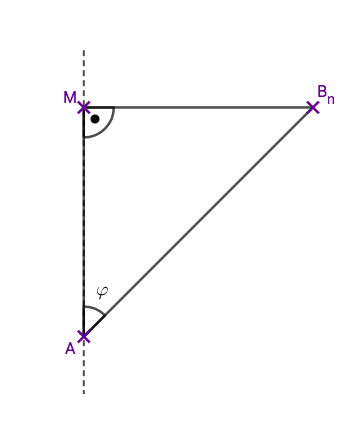
Gegeben sind rechtwinklige Dreiecke $A B_{n} M$ mit $A M = 4 cm$ und den Hypotenusen $[A B_{n}]$ .

Die Winkel $B_{n} A M$ haben das Maß $φ$ mit $φ \in] 30^{\circ}; 90^{\circ} [$ .

Der Kreis $k$ mit dem Mittelpunkt $M$ und dem Radius $r = M C = 2 cm$ schneidet die Seite $[A M]$ im Punkt $D$ und die Seiten $[B_{n} M]$ im Punkt $C$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

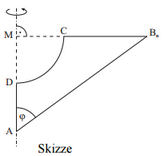
Berechnen Sie die Länge der Seite $[A B_{1}]$ für $φ = 54^{\circ}$ .

Lösung zu Teilaufgabe a
In dieser Aufgabe verwendest du die trigonometrischen Beziehungen.
Du betrachtest das rechtwinklige Dreieck $A B_{1} M$ und erinnerst dich an
$\cos (φ) = \frac{Ankathete}{Hypotenuse} .$
Im Dreieck $A B_{1} M$ ist die Strecke $[A M]$ die Ankathete und die gesuchte Strecke $[A B_{1}]$ ist die Hypotenuse. Damit formst du die Kosinusbeziehung wie folgt um:
$\cos (φ)$ $=$ $\frac{A M}{A B_{1}}$ $\cdot A B_{1}$
$\cos (φ) \cdot A B_{1}$ $=$ $A M$ $: \cos (φ)$
$A B_{1}$ $=$ $\frac{A M}{\cos (φ)}$
Da dir die Länge $A M = 4 cm$ gegeben ist, kannst du $A B_{1}$ berechnen:
$A B_{1} = \frac{A M}{\cos (φ)} = \frac{4}{\cos (54^{\circ})} \approx 6,81 (c m) .$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Figuren $A B_{n} C D$ , die durch die Strecken $[A D], [A B_{n}]$ und $[B_{n} C]$ sowie durch den Kreisbogen $\overset{⌢}{D}$ begrenzt wird, rotieren um die Gerade $A M$ .
Zeigen Sie durch Rechnung, dass für das Volumen $V$ der entstehenden Rotationskörper in Abhängigkeit von $φ$ gilt: $V (φ) = \frac{16}{3} \cdot π \cdot (4 \cdot \tan^{2} (φ) - 1) {cm}^{3}$

Lösung zu Teilaufgabe b
Du beginnst mit der Berechnung des Volumens des Rotationskörpers, welcher vom linksstehenden Dreieck $A B_{n} M$ erzeugt wird. Danach subtrahierst du das Volumen der Halbkugel, welches durch den Kreisbogen $\overset{⌢}{D}$ erzeugt wird.
Der Körper, erzeugt vom Dreieck $A B_{n} M$ , ist ein Kegel mit der Spitze $A$ , Radius $r = B_{n} M$ und Höhe $h = A M$ . Die Länge $B_{n} M$ berechnest du mittels der Tangensbeziehung
$\tan (φ) = \frac{Gegenkathete}{Ankathete} = \frac{B_{n} M}{A M} .$
Setzt du nun den Wert $A M = 4 cm$ aus der Aufgabenstellung ein und löst nach $B_{n} M$ auf, erhältst du
$B_{n} M = 4 \cdot \tan (φ) (c m) .$
Erinnere dich an die Volumenformeln für Kegel
$V_{Kegel} = \frac{π}{3} \cdot r^{2} \cdot h = \frac{π}{3} \cdot 4^{2} \cdot \tan^{2} (φ) \cdot 4 = \frac{64}{3} \cdot π \cdot \tan^{2} (φ) (c m^{3})$
und Halbkugel
$V_{Halbkugel} = \frac{1}{2} \cdot \frac{4}{3} \cdot π \cdot r^{3} = \frac{2}{3} \cdot π \cdot {M C}^{3} = \frac{16}{3} \cdot π (c m^{3}),$
wobei du den Wert für $M C$ einfach der Aufgabenstellung entnimmst. Jetzt hast du alles zusammengetragen, um das gesuchte Volumen zu berechnen:
$V (φ) = V_{Kegel} - V_{Halbkugel} = \frac{64}{3} \cdot π \cdot \tan^{2} (φ) - \frac{16}{3} \cdot π = \frac{16}{3} \cdot π (4 \cdot \tan^{2} (φ) - 1) (c m^{3}) .$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnen Sie das Volumen des entstehenden Rotationskörpers für $φ = 54^{\circ}$

Lösung zu Teilaufgabe c
In der vorigen Teilaufgabe (b) hast du bereits das Volumen
$V (φ) = V_{Kegel} - V_{Halbkugel} = \frac{16}{3} \cdot π (4 \cdot \tan^{2} (φ) - 1) (c m^{3})$
berechnet.
Setzt du nun $φ = 54 °$ in diese Formel ein, erhältst du
$V (54 °) = \frac{16}{3} \cdot π (4 \cdot \tan^{2} (54 °) - 1) = 110,21 (c m^{3}) .$
Wenn du möchtest, kannst du dir im folgenden Video noch eine Schritt-für-Schritt Lösung der Aufgabe anschauen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$\cos (φ)$	$=$	$\frac{A M}{A B_{1}}$	$\cdot A B_{1}$
$\cos (φ) \cdot A B_{1}$	$=$	$A M$	$: \cos (φ)$
$A B_{1}$	$=$	$\frac{A M}{\cos (φ)}$

Lösung zu Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung zu Teilaufgabe b

Hast du eine Frage oder Feedback?

Lösung zu Teilaufgabe c

Hast du eine Frage oder Feedback?