An einer Hauswand soll ein rechteckiger Gemüsegarten angelegt und an den drei offenen Seiten eingezäunt werden (vgl. Abbildung). Dabei bezeichnen und die Seitenlängen des Gemüsegartens in Metern. Die Gesamtlänge des Zauns soll betragen.
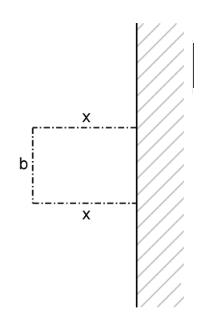
Für einen bestimmten Wert von ist der so geplante Gemüsegarten quadratisch. Berechnen Sie für diesen Fall den Flächeninhalt des Gemüsegartens.
Es wird untersucht, ob durch eine andere Wahl von bei gleichbleibender Zaunlänge ein größerer Flächeninhalt erreicht werden kann. Hierzu wird die Funktion mit betrachtet, deren Graph eine nach unten geöffnete Parabel ist.
Begründen Sie, dass der Flächeninhalt des Gemüsegartens in durch den Term beschrieben wird.
Geben Sie die beiden Nullstellen von an und bestimmen Sie so, dass der Flächeninhalt des Gemüsegartens maximal wird.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
