Gruppe A

Die Aufgaben findest du hier zum Ausdrucken als PDF

1
Geben Sie jeweils die Lösung(en) der Gleichung an.
1. $x^{2} = 100, (x \in ℝ)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Einführung in die Quadratwurzel
  $x^{2} = 100, (x \in ℝ)$
  $x = \pm \sqrt{100}$
  $x_{1} = 10$ , $x_{2} = - 10$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $x^{- 1} = 100$ , ( $x \in ℝ$ \{0})
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
  $x^{- 1} = 100, x \in ℝ$
  $x^{- 1} = \frac{1}{x}$
  $\frac{1}{x} = 100$
  $x = \frac{1}{100}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Gegeben ist die Funktion $f : x \to \frac{4}{x + 3} - 2$ mit dem Definitionsbereich $ℝ$ \{ $- 3$ }.
1. Zeigen Sie rechnerisch, dass $- 1$ Nullstelle von $f$ ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  $f (x) = \frac{4}{x + 3} - 2;$
  Nullstelle: $f (x) = 0$
  $f (- 1) = \frac{4}{- 1 + 3} - 2 = \frac{4}{2} - 2 = 0$
  $\Rightarrow$ $- 1$ ist eine Nullstelle der Funktion $f$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Beschreiben Sie, wie der Graph von $f$ durch Verschieben aus dem Graphen der in $ℝ$ \{ $0$ } definierten Funktion $g : x \to \frac{4}{x}$ hervorgeht.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen verschieben
  $g (x) = \frac{4}{x}$
  $f (x) = \frac{4}{x + 3} - 2$
  Durch ersetzen von $x$ durch $x + 3$ wird der Graph um $3$ nach links, in die negative
  x-Richtung verschoben.
  Durch die Subtraktion von $- 2$ wird der Graph um $2$ nach unten, in die negative
  y-Richtung verschoben.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
An einer Hauswand soll ein rechteckiger Gemüsegarten angelegt und an den drei offenen Seiten eingezäunt werden (vgl. Abbildung). Dabei bezeichnen $x$ und $b$ die Seitenlängen des Gemüsegartens in Metern. Die Gesamtlänge des Zauns soll $12 m$ betragen.
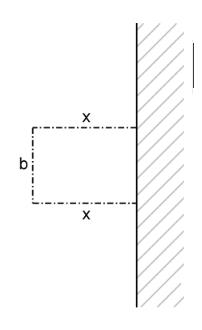
1. Für einen bestimmten Wert von $x$ ist der so geplante Gemüsegarten quadratisch. Berechnen Sie für diesen Fall den Flächeninhalt des Gemüsegartens.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat
  Damit der Garten quadratisch ist, müssen die Seiten $x$ und $b$ gleich lang sein.
  Laut Aufgabenstellung gilt: $2 \cdot x + b = 12$
  Mit $b = x$ ist also $2 \cdot x + x = 12$
  $\Rightarrow 3 \cdot x = 12$
  $\Rightarrow x = 4$
  Mit $x = b = 4$ hat der Gemüsegarten $4$ gleich lange Seiten und ist somit quadratisch.
  Die Fläche beträgt dann $(4 m)^{2} = 16 m^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ein quadratischer Garten hat gleich lange Seiten.
2. Es wird untersucht, ob durch eine andere Wahl von $x$ bei gleichbleibender Zaunlänge ein größerer Flächeninhalt erreicht werden kann. Hierzu wird die Funktion $f$ mit $f (x) = x \cdot (12 - 2 x)$ betrachtet, deren Graph eine nach unten geöffnete Parabel ist.
  Begründen Sie, dass der Flächeninhalt des Gemüsegartens in $m^{2}$ durch den Term $f (x)$ beschrieben wird.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
  Aus der Aufgabenstellung ist bekannt: $2 \cdot x + b = 12$ $\Rightarrow$
  $b = 12 - 2 \cdot x$
  $A_{Rechteck} = x \cdot b$
  $A_{Rechteck} = x \cdot (12 - 2 \cdot x)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Geben Sie die beiden Nullstellen von $f$ an und bestimmen Sie $x$ so, dass der Flächeninhalt des Gemüsegartens maximal wird.
  
  $f (x) = x \cdot (12 - 2 x)$
  1. Nullstellen:
  Für eine Nullstelle gilt: $f (x) = 0$
  $x \cdot (12 - 2 x) = 0$
  Ein Produkt ist 0, wenn einer der Faktoren 0 ist.
  1. Faktor: $x = 0$
  2. Faktor: $12 - 2 x = 0$ $\Rightarrow$ $x = 6$
  Die Nullstellen der Funktion $f$ sind $0$ und $6$ .
  2. Scheitelpunkt:
  Die Funktion $f$ ist eine nach unten geöffnete Parabel mit den Nullstelle $0$ und $6$ . Der Scheitelpunkt der Funktion $f$ liegt genau zwischen den beiden Nullstellen. $\Rightarrow$
  $x = \frac{1}{2} \cdot (0 + 6) = 3$
  Für $x = 3$ ist der Flächeninhalt des Gemüsegartens maximal.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Nullstellen von $f$ .
  Bestimme den Scheitelpunkt von $f .$
4
Die Kinder der sechsten Klassen eines Gymnasiums haben als zweite Fremdsprache entweder Latein oder Französisch gewählt. Unter den Kindern wird eines zufällig ausgewählt. Betrachtet werden folgende Ereignisse:
L: Das Kind hat Latein gewählt.
M: Das Kind ist ein Mädchen
1. Bei einer der folgenden Vierfeldertafeln passt der grau gefärbte Bereich zum Ereignis „Genau eines der beiden Ereignisse L und M tritt ein.“. Kreuzen Sie (nur) diese an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
  In der vierten Vierfeldertafel ganz rechts passt der grau gefärbte Bereich zum Ereignis „Genau eines der beiden Ereignisse L und M tritt ein".
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
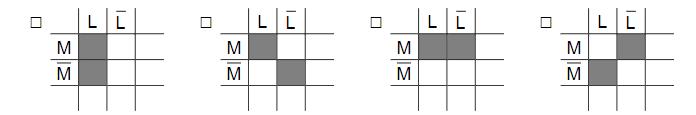
2. Eine der folgenden Mengenschreibweisen gehört zum Ereignis „Ein Kind hat Französisch gewählt und ist kein Mädchen.“ Kreuzen Sie (nur) diese an.
  $L \cap M$
  $L \cup M$
  $L \cap M$
  $L \cup M$
  $L \cap M$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verknüpfungen von Mengen
  $L \cap M$ : Hat Latein gewählt und ist kein Mädchen
  $L \cup M$ : Hat Latein gewählt oder ist kein Mädchen
  $L \cap M$ : Hat Französisch gewählt und ist kein Mädchen
  $L \cup M$ : Hat Französisch gewählt oder ist kein Mädchen
  $L \cap M$ : Alle, die keine Mädchen sind, das Latein gewählt hat
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Seit Dezember 2017 führt eine neue Seilbahn auf die Zugspitze.
1. Eine Gondel dieser Seilbahn bietet Platz für $120$ Personen. Geben Sie die Anzahl der Personen in der Gondel an, wenn diese bezüglich der Personenzahl zu $30$ % ausgelastet ist .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
  $120 \hat{=} 100$ %
  $12 \hat{=} 10$ %
  $3 \cdot 12 = 36 \hat{=} 30$ %
  Mit $36$ Personen ist eine Gondel zu $30$ % ausgelastet.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Seilbahn überwindet einen Höhenunterschied von $h = 1945$ . Nimmt man vereinfachend an, dass die Fahrstrecke der Länge $l = 4467$ geradlinig verläuft, so schließen das Seil und die Horizontale einen Steigungswinkel $α$ ein (vgl. Abbildung)
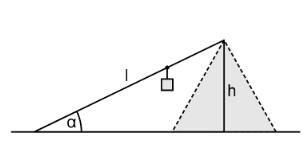
  Geben Sie eine Gleichung an, durch die der Steigungswinkel $α$ aus $l$ und $h$ berechnet werden kann.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
  $\sin (α)$ beschreibt das Verhältnis von Seitenlängen in einem rechtwinkligen Dreieck in Abhängigkeit von einem spitzen Winkel $α$ wie folgt:
  $\sin (α) = \frac{Gegenkathete}{Hypotenuse}$
  $\sin (α) = \frac{h}{l}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. In der Realität variiert die Steigung von Bergbahnen im Streckenverlauf. So ist der maximale Steigungswinkel der Zugspitzseilbahn deutlich größer als der Wert, der sich aus Aufgabe 5b ergeben würde. Nachfolgende Tabelle gibt die maximalen Steigungen und die zugehörigen Steigungswinkel für die Seilbahn und für die ebenfalls auf die Zugspitze führende Zahnradbahn an.
  Ergänzen Sie folgende Erläuterung:
  Die Steigung einer Seilbahn oder Schiene ist wie die Steigung einer Gerade im Koordinatensystem festgelegt. Eine Steigung von $0,25$ bedeutet beispielsweise, dass bei einer horizontalen Entfernung von ________ m eine Höhendifferenz von ________ m überwunden wird.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentangaben bei Steigungen
  0,25 $\hat{=} 25$ %
  Dies bedeutet, dass die senkrecht zurückgelegte Strecke $25$ % von der waagrecht zurückgelegten Strecke ausmacht.
  Bei einer horizontalen Entfernung von $100$ m wird eine Höhendifferenz von $25$ m überwunden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Die maximale Steigung ist nicht direkt proportional zum zugehörigen Steigungswinkel. Beschreiben Sie unter Einbeziehung der konkreten Werte aus obiger Tabelle, wie man dies zeigen könnte.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Direkte Proportionalität
  Zwei Größen sind dann direkt proportional zueinander, wenn die eine Größe aus der anderen hervorgeht, indem man sie mit dem gleichen Faktor multipliziert.
  1. Zeile: $\frac{1,04}{0,25} = 4,16$
  2. Zeile: $\frac{46}{14} \approx 3,29$
  $4,16 \neq 3,29$
  Da die beiden Quotienten nicht gleich sind, ist die maximale Steigung ist nicht direkt proportional zum zugehörigen Steigungswinkel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne den Quotienten der Werte in den beiden Spalten der ersten Zeile der Tabelle und den Quotienten der Werte in den beiden Spalten der zweiten Zeile der Tabelle und vergleiche diese miteinander.
6
Lösen Sie folgende Aufgaben.
1. Ein Dreieck mit einer Seite der Länge $4 c m$ und zugehöriger Höhe $h$ hat den Flächeninhalt $6 c m^{2}$ . Berechnen Sie $h$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Dreiecks
  $A = \frac{1}{2} \cdot g \cdot h$
  $6 = \frac{1}{2} \cdot 4 \cdot h$
  $h = 3$
  Die Höhe $h$ des Dreiecks ist 3cm.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Verwende die Flächenformel für das Dreieck
  Setze die bekannten Werte ein
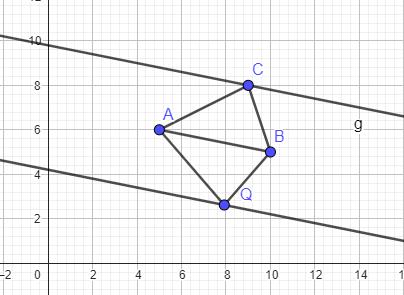
2. Betrachtet wird ein Dreieck $A B C$ . Die Gerade $g$ verläuft parallel zur Gerade $A B$ durch den Punkt $C$ (vgl. Abbildung).
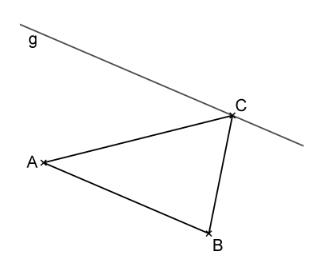
  Spiegelt man $g$ an $A B$ , erhält man die Bildgerade $g^{'}$ .
  Zeichnen Sie $g^{'}$ ein und begründen Sie:
  Ist $Q$ ein beliebiger Punkt auf $g^{'}$ , so hat das Dreieck $A Q B$ den gleichen Flächeninhalt wie das Dreieck $A B C$ .
  
  Alle Dreiecke mit der Grundlinie $A B$ und einem beliebigegen Punkt $Q$ auf $g^{'}$ haben aufgrund der Symmetrie die selbe Höhe wie das Dreieck $A B C$ . Somit hat jedes beliebige Dreieck $A B Q$ die selbe Fläche wie das Dreieck $A B C$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Die Abbildung zeigt ein rechtwinkliges Dreieck mit drei Halbkreisen, die jeweils eine der Dreiecksseiten als Durchmesser haben.
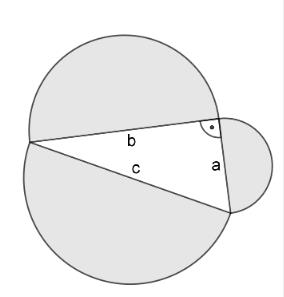
Begründen Sie mithilfe einer Rechnung, dass die Summe der Flächeninhalte der beiden kleineren Halbkreise gleich dem Flächeninhalt des größten Halbkreises ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
Satz des Pythagoras: $a^{2} + b^{2} = c^{2}$
Flächeninhalt eines Kreises: $A = \frac{1}{4} \cdot d^{2} \cdot π$
$\frac{1}{4} \cdot a^{2} \cdot π + \frac{1}{4} \cdot b^{2} \cdot π = \frac{1}{4} \cdot π \cdot (a^{2} + b^{2}) = \frac{1}{4} \cdot π \cdot c^{2}$
Addiere die Flächen der beiden kleinen Kreise und klammere aus. Fasse mit Hilfe des Satzes von Pythagoras zusammen.