Aufgabe 5
Batterien für Elektroautos speichern unterschiedlich viel Energie.
Um die Batteriepreise vergleichen zu können, wird der Preis in Euro pro Kilowattstunde (kWh) angegeben. Der Graph beschreibt die Entwicklung des Batteriepreises.
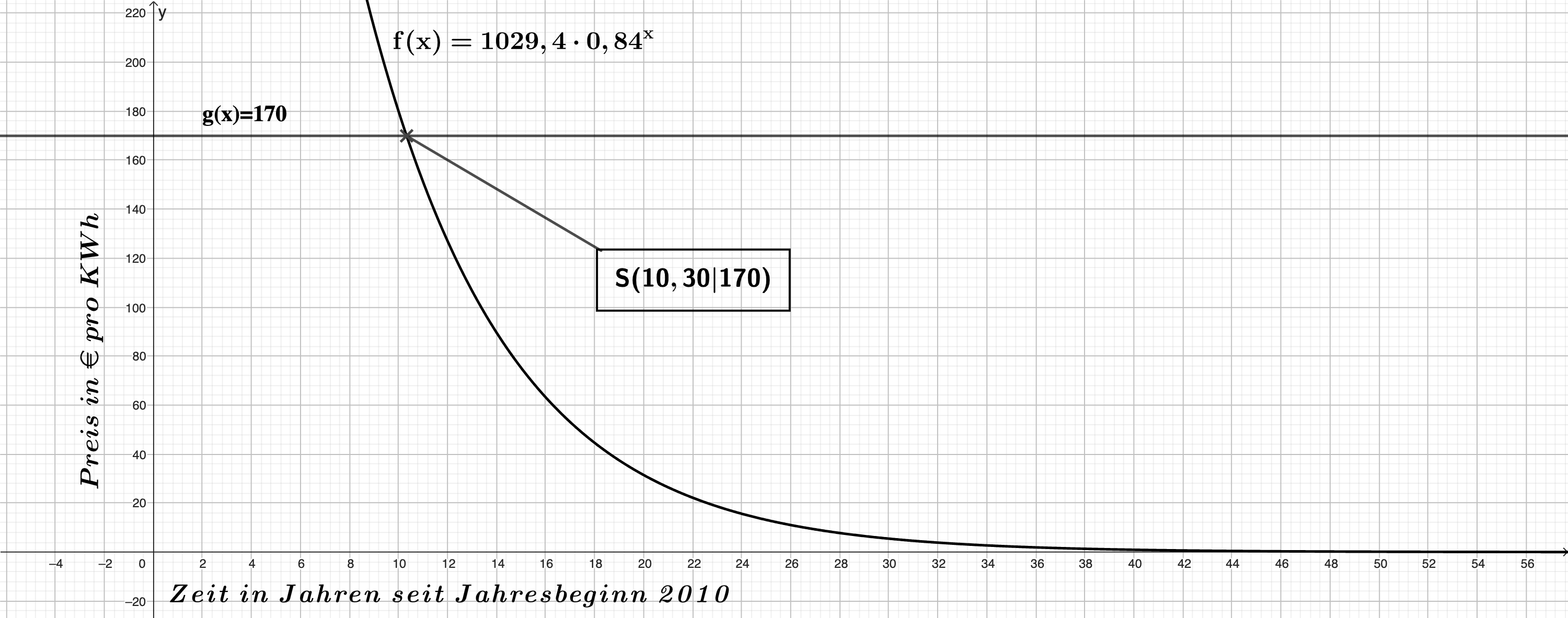
Ralf hat eine Modellierung für die Preise von 2010 bis 2015 vorgenommen und folgende Funktionsgleichung aufgestellt.
Erkläre die Bedeutung der Zahlen und sowie von und im Sachzusammenhang. (2 BE)
In der Abbildung ist der Punkt eingetragen.
Erkläre die Bedeutung des Punktes im Sachzusammenhang. (1 BE)
Berechne mithilfe der Funktion den voraussichtlichen Batteriepreis pro zu Beginn des Jahres . (2 BE)
Berechne mithilfe von Ralfs Modell den Batteriepreis pro kWh zu Beginn des Jahres 2008. (2 BE)
Die Kosten für die Batterie bestimmen stark die Kosten für das Elektroauto. Laut Experten werden Elektroautos günstiger als mit Benzin fahrende Autos, sobald der Batteriepreis unter pro kWh fällt.
Bestimme, in welchem Jahr der Preis voraussichtlich erstmals unter liegt. (3 BE)
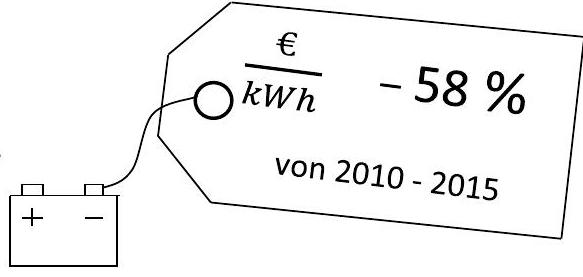
Ralf findet eine Abbildung zur Entwicklung des Batteriepreises.
Überprüfe, ob die Funktion zu dieser Angabe passt. (3 BE)
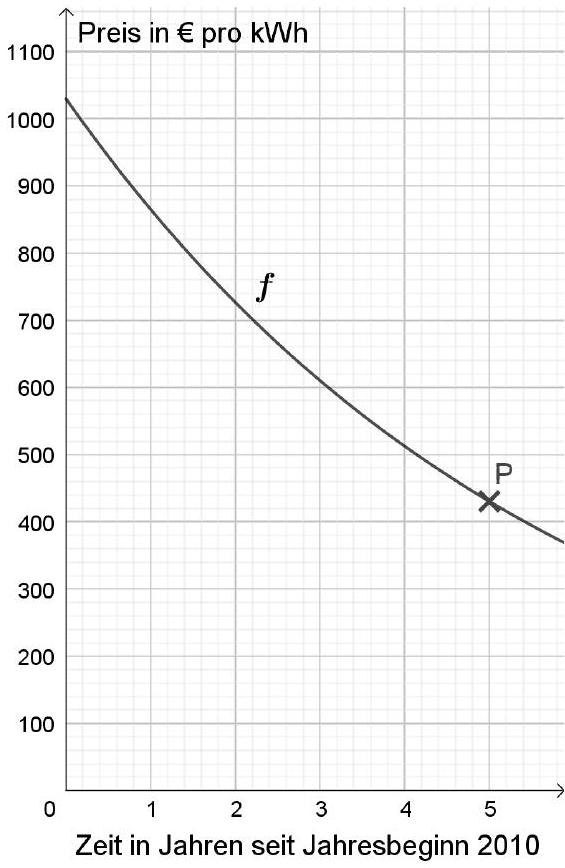
Zu Beginn des Jahres 2021 lag der tatsächliche Batteriepreis bei pro kWh.
Yasmin stellt fest, dass der Preis nicht zu Ralfs Modellierung passt.
Berechne, um wie viel Euro Ralfs Modellierung vom tatsächlichen Preis abweicht. (2 BE)
Im Koordinatensystem ist der Ladevorgang einer Batterie dargestellt.
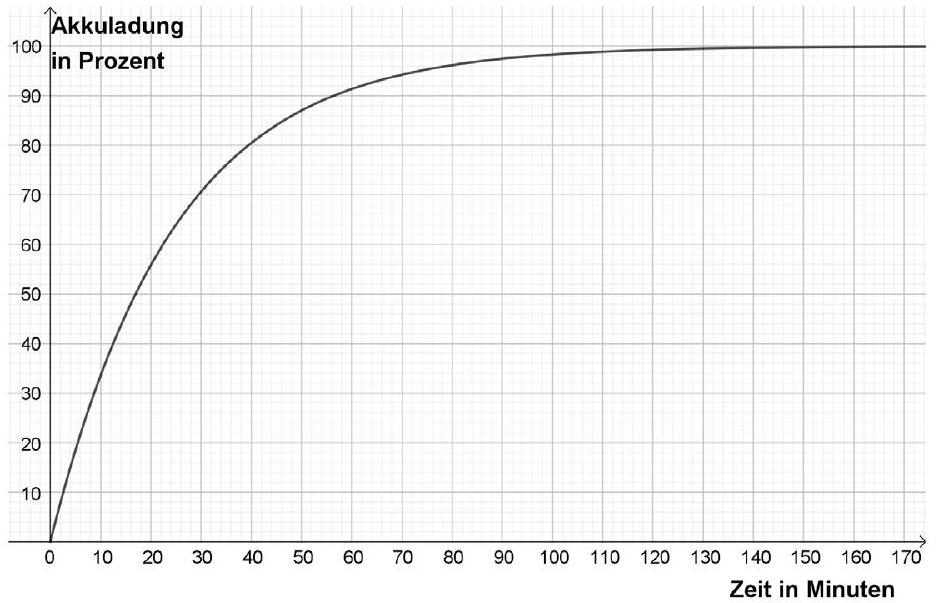
Beschreibe mithilfe des Graphen den Ladevorgang. (2 BE)
Begründe, warum es sich beim Ladevorgang um kein exponentielles Wachstum handelt. (1 BE)
Der Graph kann mit beschrieben werden.
Begründe, dass die Funktion nie den Wert erreicht. (2 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen