Aufgabe 4
Krokusse und Osterglocken wachsen aus Zwiebeln.
Von den Zwiebeln der Osterglocken wachsen an.
Von 25 Krokus-Zwiebeln wachsen 21 an.
Berechne, wie viel Prozent der Krokusse anwachsen. (1 BE)
Eine Stadt kauft Osterglocken-Zwiebeln und Krokus-Zwiebeln.
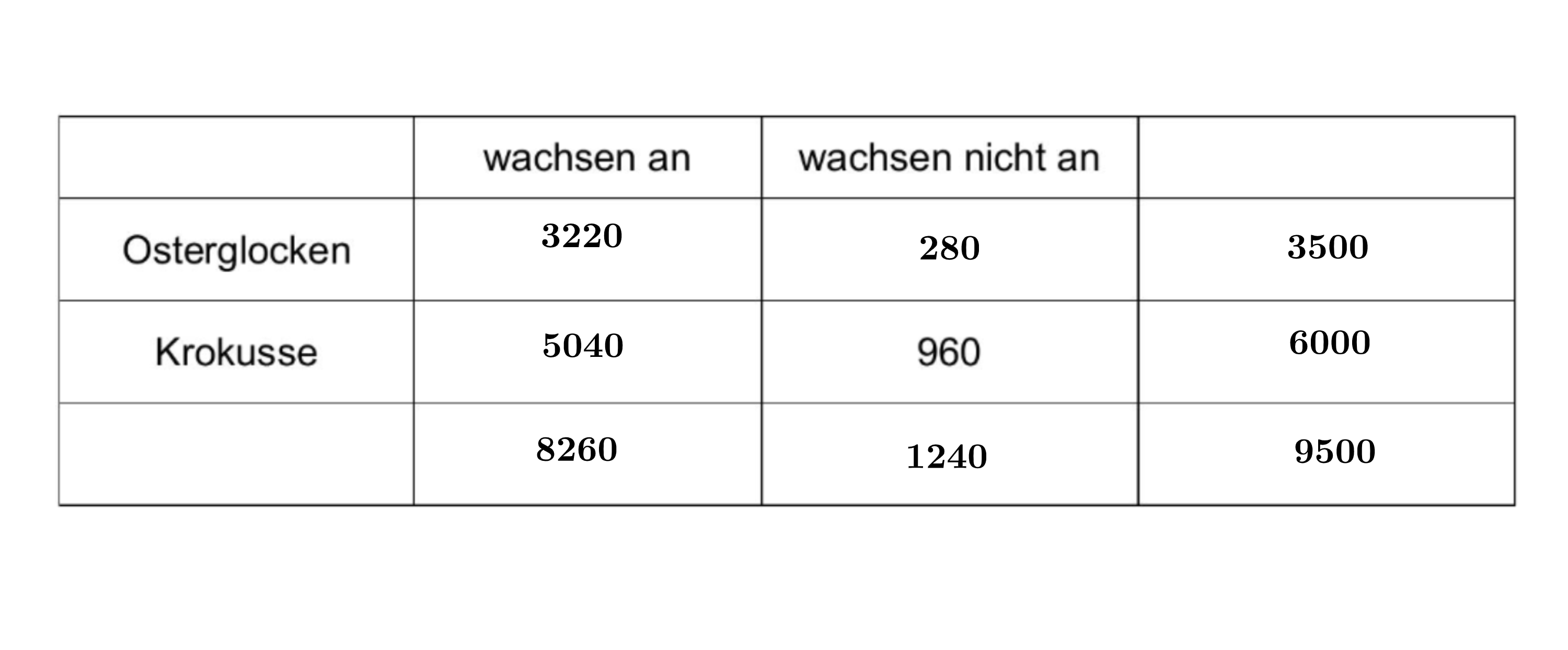
In der Vierfeldertafel ist der Wert eingetragen.
Erkläre die Bedeutung im Sachzusammenhang.
Gib an, wie der Wert berechnet werden kann. (2 BE)

Vervollständige die Vierfeldertafel. (4 BE)
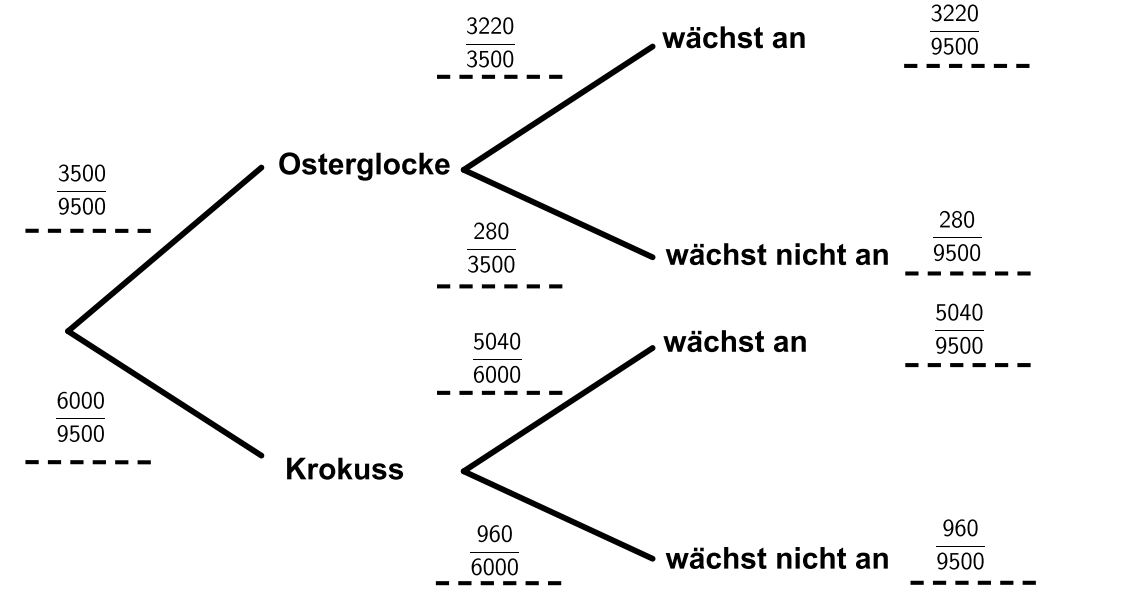
Eine der gekauften Zwiebeln wird zufällig ausgewählt.
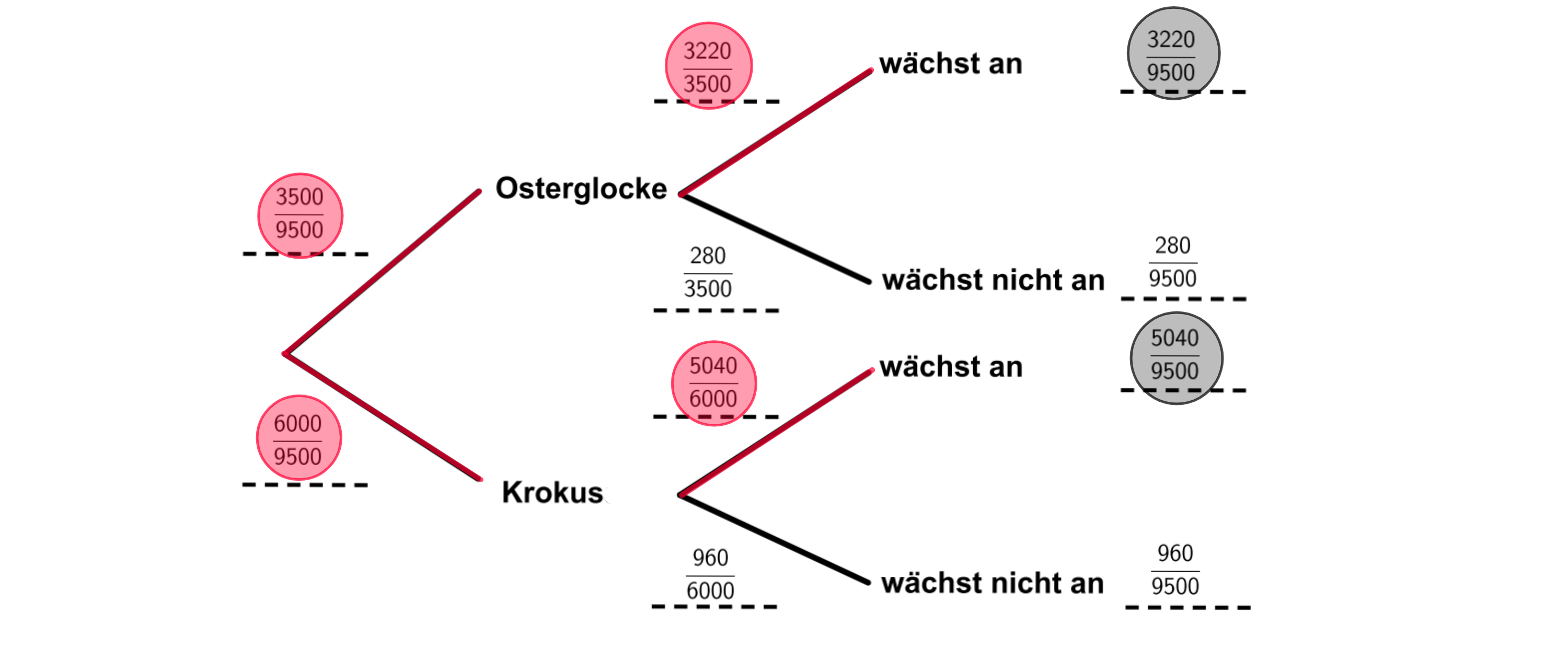
Vervollständige das Baumdiagramm. (4 BE)
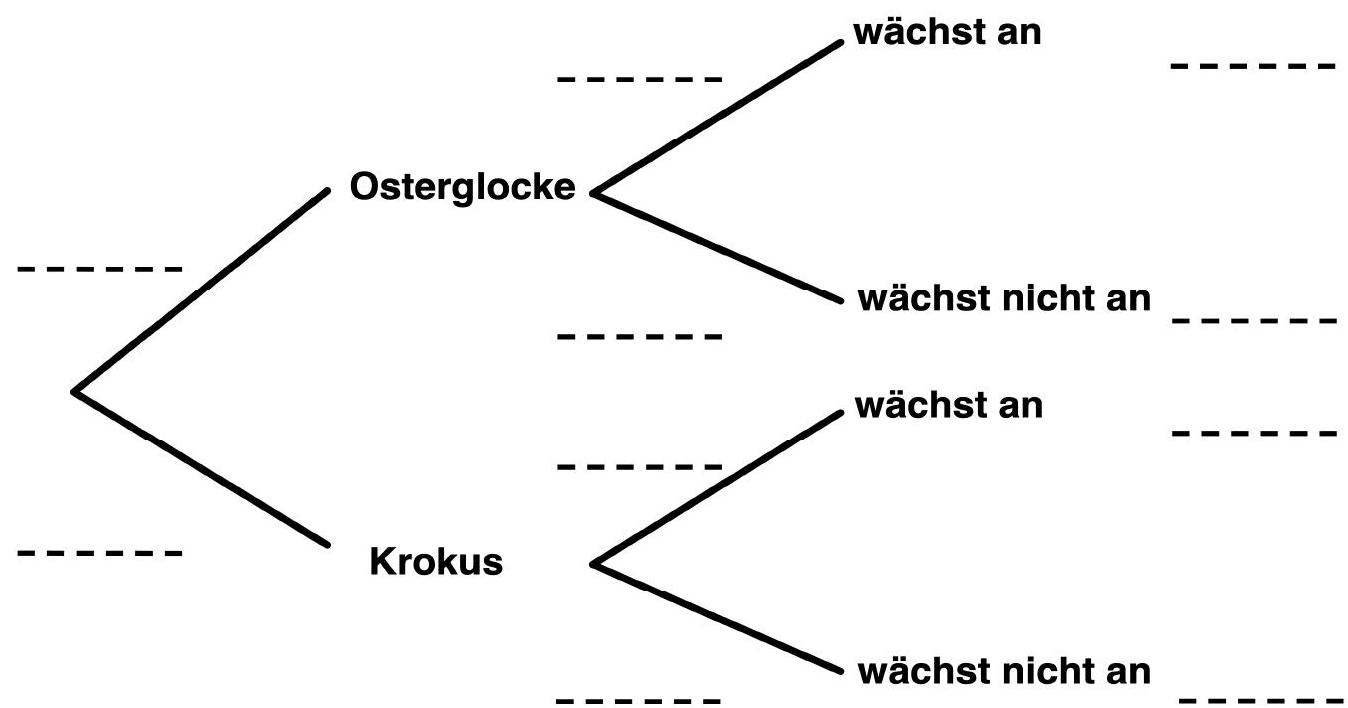
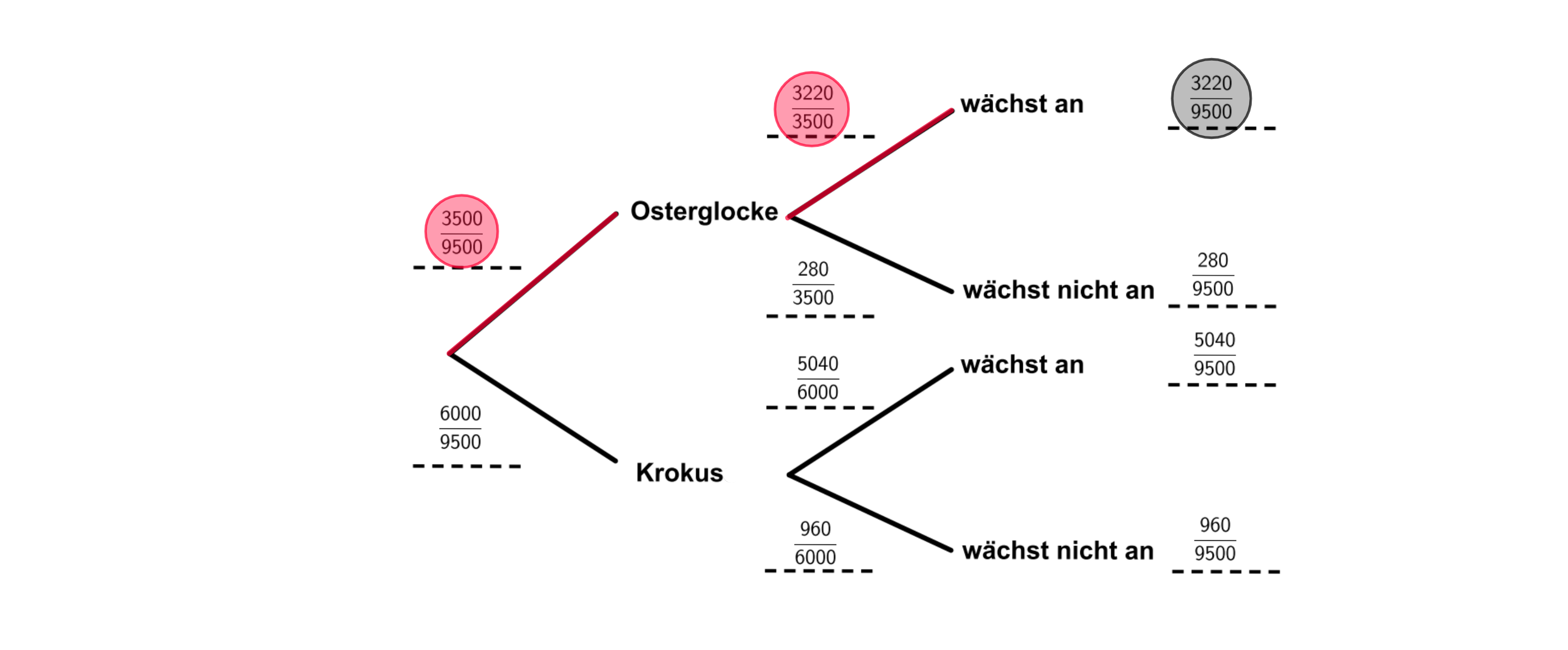
Gib die Wahrscheinlichkeit an, dass eine zufällig ausgewählte Zwiebel eine Osterglocke ist und anwächst. (1 BE)
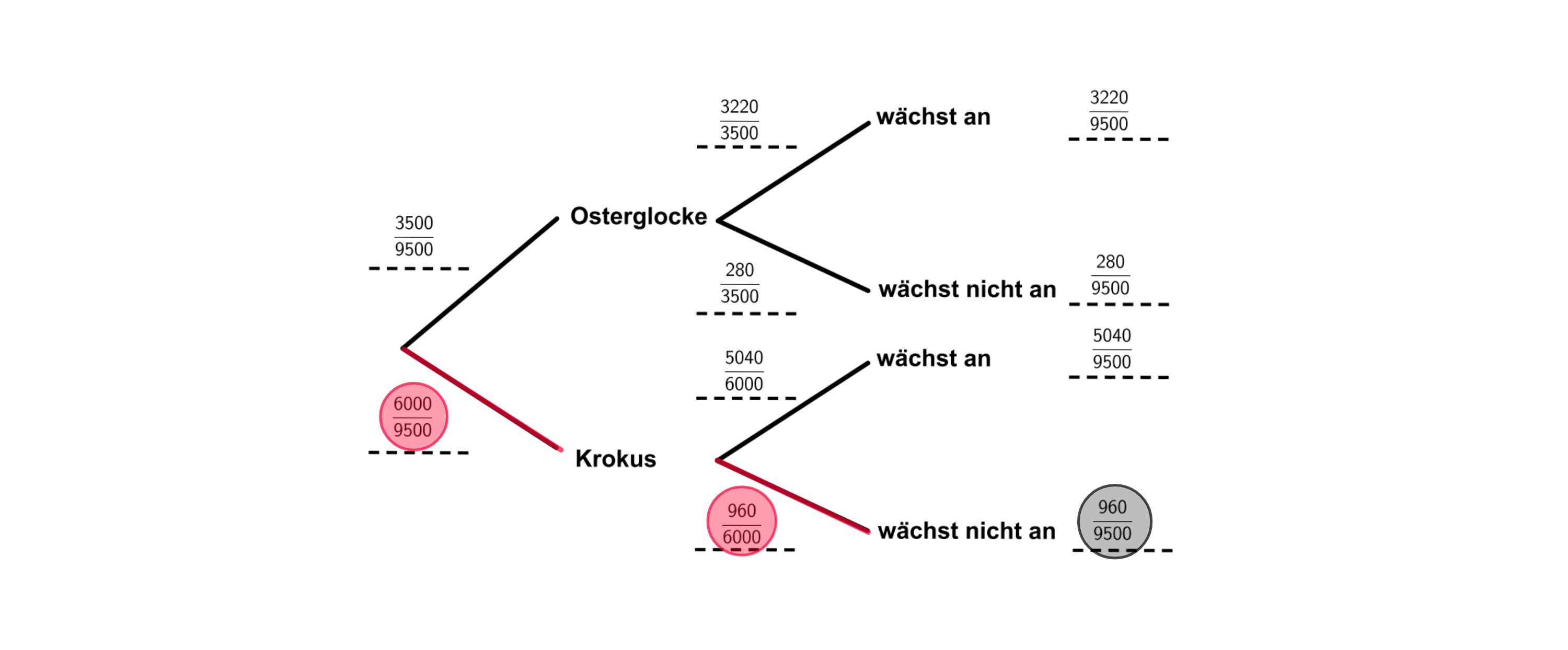
Gib die Wahrscheinlichkeit an, dass ein Krokus nicht anwächst. (1 BE)
Bestimme die Wahrscheinlichkeit, dass eine Zwiebel anwächst.
Gib die Wahrscheinlichkeit in Prozent an. (2 BE)
Eine Zwiebel wächst an.
Gib die Wahrscheinlichkeit an, dass die Zwiebel ein Krokus ist. (2 BE)
Von den Zwiebeln werden zufällig ausgewählte Zwiebeln in ein Blumenbeet gepflanzt. Berechne, wie viele anwachsende Krokusse man erwarten kann.
Entscheide, ob man mehr angewachsene Krokusse als Osterglocken erwarten kann.
(3 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen